二次函数(2)[下学期]
图片预览




文档简介
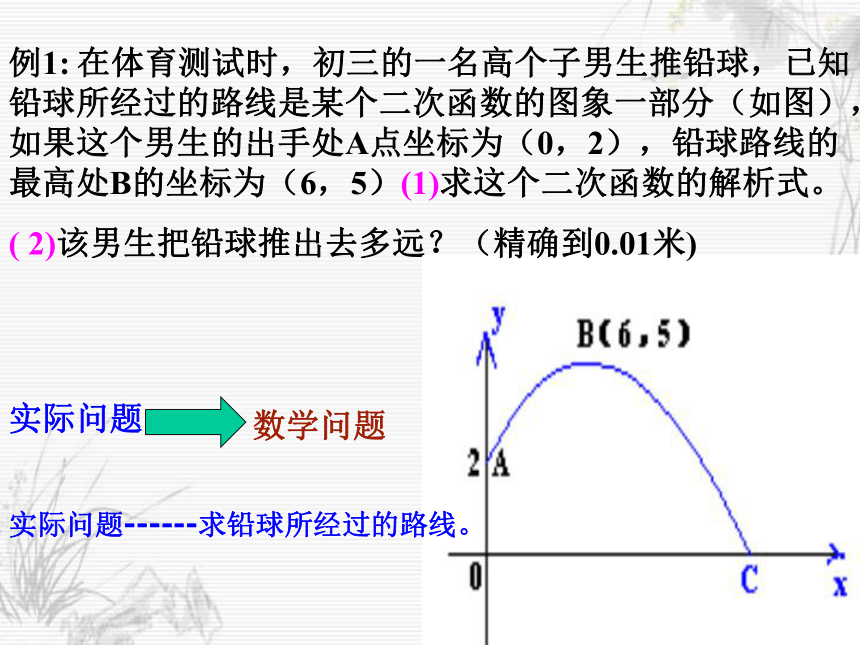
课件19张PPT。二次函数(复习2)例1: 在体育测试时,初三的一名高个子男生推铅球,已知铅球所经过的路线是某个二次函数的图象一部分(如图),如果这个男生的出手处A点坐标为(0,2),铅球路线的最高处B的坐标为(6,5)(1)求这个二次函数的解析式。
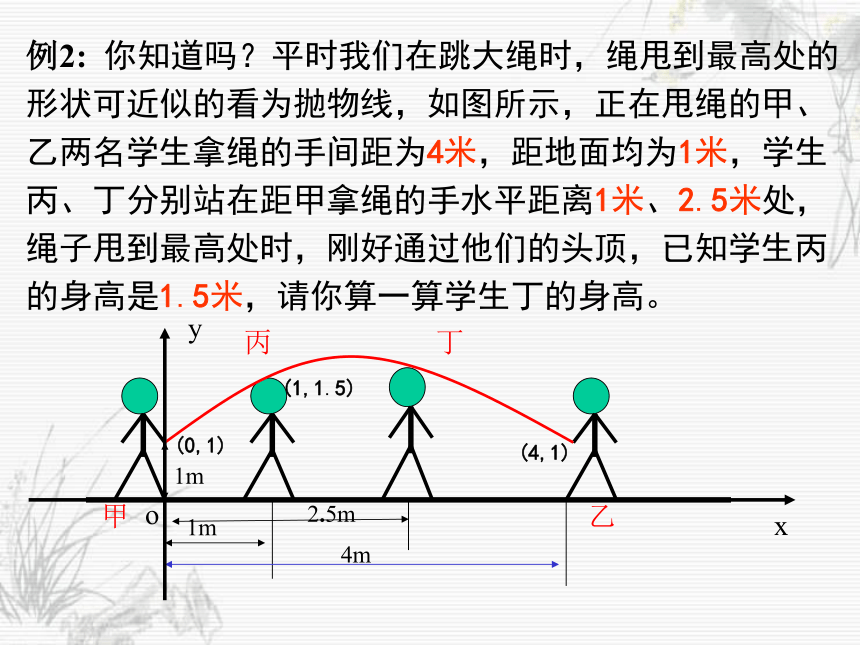
( 2)该男生把铅球推出去多远?(精确到0.01米)实际问题数学问题实际问题------求铅球所经过的路线。例2: 你知道吗?平时我们在跳大绳时,绳甩到最高处的形状可近似的看为抛物线,如图所示,正在甩绳的甲、乙两名学生拿绳的手间距为4米,距地面均为1米,学生丙、丁分别站在距甲拿绳的手水平距离1米、2.5米处,绳子甩到最高处时,刚好通过他们的头顶,已知学生丙的身高是1.5米,请你算一算学生丁的身高。
1m2.5m4m1m甲乙丙丁(0,1)(4,1)(1,1.5)例3. 杭州某公司生产的新产品,它的成本是2元/件,售价是3元/件,年销售量为10万件,为了获得更好的效益,公司准备拿出一定的资金做广告。根据经验,每年投入的广告费是 x (万元)时,产品的年销售量将是原销售量的y倍,且y是x的二次函数,它们的关系如下表:(1)求y与x的函数的关系式;(2)如果利润=销售总额-成本费-广告费,试写出年利润S(万元)与广告费x(万元)的函数关系式;并求出当广告费x为多少万元时,年利润S最大。例5 : 如图,在梯形ABCD中,AB//DC,ADAB,已知
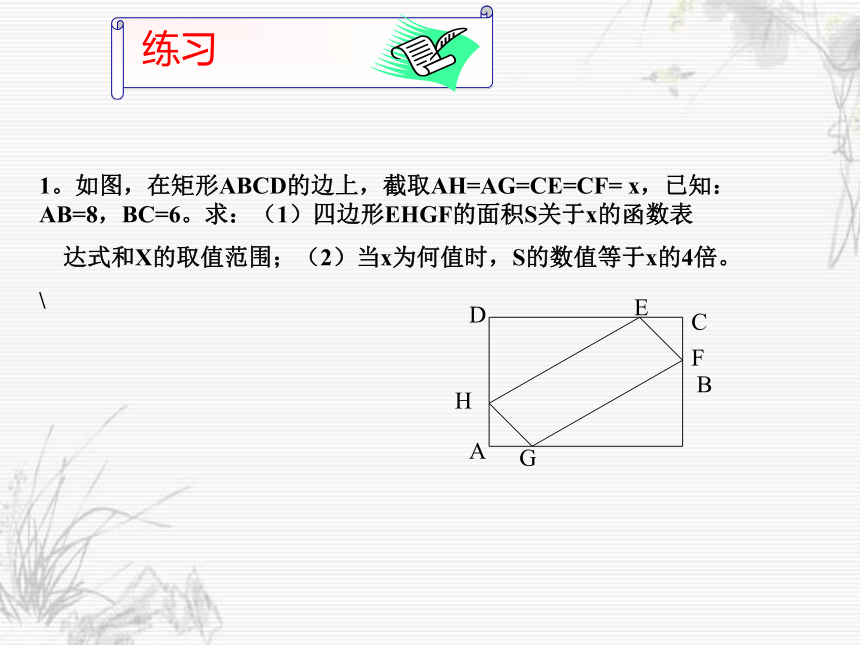
AB=6,CD=4,AD=2,现在梯形内作一内接矩形
AEFG,使E在AB上,F在BC上,G在AD上。
(1)设EF=x,试求矩形AEFG的面积S关于x的函数
关系式; (2)画出函数S的图象; (3)当x为
何值时, S有最大值?并求出S的最大值。
例6 把长为20㎝的铁丝弯成半径为R的一个扇形,
(1)试写出扇形面积S与半径R的函数关系式;
(2)求扇形的半径R的取值范围; (3)当R为
多长时,扇形的面积最大,其最大面积是多少?B
2:在ABC中AB=4,AC=6,BC=2,P是AC上与A,C不重合的一动点,过P,B,C的⊙O交AB于D,
① 设PA=x,PC+PD=y,求y与x的函数关系式,并确定x的范围;
②P在AC上何处时函数y有最小值,最小值是多少?
③求当y取最小值时⊙Ο的面积。
B
D
C A
P
3:某商场将进价40元一个的某种商品按50元一个售出时,能卖出500个,已知这种商品每个涨价一元,销量减少10个,为赚得最大利润,售价定为多少?最大利润是多少?4:如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米。
(1)求S与x的函数关系式及自变量的取值范围;
(2)当x取何值时所围成的花圃面积最大,最大值是多少?
(3)若墙的最大可用长度为8米,则求围成花圃的最大面积。 5。 如图,在ΔABC中,AB=8cm,BC=6cm,∠B=90°,
点P从点A开始沿AB边向点B以2厘米/秒的速度移动,
点Q从点B开始沿BC边向点C以1厘米/秒的速度
移动,如果P,Q分别从A,B同时出发,
几秒后ΔPBQ的面积最大?
最大面积是多少?PQ 6。如图,一位运动员在距篮下4米处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.
(1)建立如图所示的直角坐标系,求抛物线的表达式;
(2)该运动员身高1.8米,在这次跳投中,球在头顶上方0.25米处出手,问:球出手时,他跳离地面的高度是多少。 7:某企业投资100万元引进一条产品加工生产线,若不计维修、保养费用,预计投产后每年可创利33万。该生产线投产后,从第1年到第x年的维修、保养费用累计为y(万元),且y=ax2+bx,若第1年的维修、保养 费用为2万元,第2年为6万元。
(1)求y的解析式;
(2)投产后,这个企业在第几年就能收回投资? 8。 如图所示,已知抛物线与x轴相交于两点A ,B 与y轴负半轴相交于点C,若抛物线顶点P的横坐标是1,A、B两点间的距离为4,且△ABC的面积为6。(1)求点A和B的坐标(2)求此抛物线的解析式(3)求四边形ACPB的面积
9。 如图,已知抛物线y=ax2+4ax+t(a>0)交x轴于A、B两点,交y轴于点C,点B的坐标为(-1,0).
(1)求此抛物线的对称轴及点A的坐标(2)过点C作x轴的平行线交抛物线的对称轴于点P,你能判断四边形ABCP是什么四边形吗?请证明你的结论;(3)连结AC、BP,若AC ⊥BP,求此抛物线的解析式10:如图,已知正方形ABCD的边长为4,E是BC上的
点,F是CD上的点,且EC=AF,EC=x,ΔAEF的
面积为y。
(1)求y与x之间的函数关系式和自变量x的取值范围 ;
(2)画出函数的图象。
11。 如图是某公园一圆形喷水池,水流在各方向沿形
状相同的抛物线落下,如果喷头所在处A(0,1.25),水流路
线最高处B(1,2.25),则该抛物线的解析式为____________
如果不考虑其他因素,那么水池的半径至少要____米,才能使
喷出的水流不致落到池外。y= -(x-1)2 +2.252.5 有一块铁皮拱形边缘呈抛物线状, MN=4,抛
物线的顶点处到MN的距离是 4,要 在 铁皮上截
下一矩形ABCD,是矩形的顶点B、C落在 MN 上,
点A、D 落在抛物线上,问这样截下去的矩形铁
皮的周长能否等于 8,若能,求出矩形的长和宽。
若不能,说明理由。0MNABCDp再见
( 2)该男生把铅球推出去多远?(精确到0.01米)实际问题数学问题实际问题------求铅球所经过的路线。例2: 你知道吗?平时我们在跳大绳时,绳甩到最高处的形状可近似的看为抛物线,如图所示,正在甩绳的甲、乙两名学生拿绳的手间距为4米,距地面均为1米,学生丙、丁分别站在距甲拿绳的手水平距离1米、2.5米处,绳子甩到最高处时,刚好通过他们的头顶,已知学生丙的身高是1.5米,请你算一算学生丁的身高。
1m2.5m4m1m甲乙丙丁(0,1)(4,1)(1,1.5)例3. 杭州某公司生产的新产品,它的成本是2元/件,售价是3元/件,年销售量为10万件,为了获得更好的效益,公司准备拿出一定的资金做广告。根据经验,每年投入的广告费是 x (万元)时,产品的年销售量将是原销售量的y倍,且y是x的二次函数,它们的关系如下表:(1)求y与x的函数的关系式;(2)如果利润=销售总额-成本费-广告费,试写出年利润S(万元)与广告费x(万元)的函数关系式;并求出当广告费x为多少万元时,年利润S最大。例5 : 如图,在梯形ABCD中,AB//DC,ADAB,已知
AB=6,CD=4,AD=2,现在梯形内作一内接矩形
AEFG,使E在AB上,F在BC上,G在AD上。
(1)设EF=x,试求矩形AEFG的面积S关于x的函数
关系式; (2)画出函数S的图象; (3)当x为
何值时, S有最大值?并求出S的最大值。
例6 把长为20㎝的铁丝弯成半径为R的一个扇形,
(1)试写出扇形面积S与半径R的函数关系式;
(2)求扇形的半径R的取值范围; (3)当R为
多长时,扇形的面积最大,其最大面积是多少?B
2:在ABC中AB=4,AC=6,BC=2,P是AC上与A,C不重合的一动点,过P,B,C的⊙O交AB于D,
① 设PA=x,PC+PD=y,求y与x的函数关系式,并确定x的范围;
②P在AC上何处时函数y有最小值,最小值是多少?
③求当y取最小值时⊙Ο的面积。
B
D
C A
P
3:某商场将进价40元一个的某种商品按50元一个售出时,能卖出500个,已知这种商品每个涨价一元,销量减少10个,为赚得最大利润,售价定为多少?最大利润是多少?4:如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米。
(1)求S与x的函数关系式及自变量的取值范围;
(2)当x取何值时所围成的花圃面积最大,最大值是多少?
(3)若墙的最大可用长度为8米,则求围成花圃的最大面积。 5。 如图,在ΔABC中,AB=8cm,BC=6cm,∠B=90°,
点P从点A开始沿AB边向点B以2厘米/秒的速度移动,
点Q从点B开始沿BC边向点C以1厘米/秒的速度
移动,如果P,Q分别从A,B同时出发,
几秒后ΔPBQ的面积最大?
最大面积是多少?PQ 6。如图,一位运动员在距篮下4米处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.
(1)建立如图所示的直角坐标系,求抛物线的表达式;
(2)该运动员身高1.8米,在这次跳投中,球在头顶上方0.25米处出手,问:球出手时,他跳离地面的高度是多少。 7:某企业投资100万元引进一条产品加工生产线,若不计维修、保养费用,预计投产后每年可创利33万。该生产线投产后,从第1年到第x年的维修、保养费用累计为y(万元),且y=ax2+bx,若第1年的维修、保养 费用为2万元,第2年为6万元。
(1)求y的解析式;
(2)投产后,这个企业在第几年就能收回投资? 8。 如图所示,已知抛物线与x轴相交于两点A ,B 与y轴负半轴相交于点C,若抛物线顶点P的横坐标是1,A、B两点间的距离为4,且△ABC的面积为6。(1)求点A和B的坐标(2)求此抛物线的解析式(3)求四边形ACPB的面积
9。 如图,已知抛物线y=ax2+4ax+t(a>0)交x轴于A、B两点,交y轴于点C,点B的坐标为(-1,0).
(1)求此抛物线的对称轴及点A的坐标(2)过点C作x轴的平行线交抛物线的对称轴于点P,你能判断四边形ABCP是什么四边形吗?请证明你的结论;(3)连结AC、BP,若AC ⊥BP,求此抛物线的解析式10:如图,已知正方形ABCD的边长为4,E是BC上的
点,F是CD上的点,且EC=AF,EC=x,ΔAEF的
面积为y。
(1)求y与x之间的函数关系式和自变量x的取值范围 ;
(2)画出函数的图象。
11。 如图是某公园一圆形喷水池,水流在各方向沿形
状相同的抛物线落下,如果喷头所在处A(0,1.25),水流路
线最高处B(1,2.25),则该抛物线的解析式为____________
如果不考虑其他因素,那么水池的半径至少要____米,才能使
喷出的水流不致落到池外。y= -(x-1)2 +2.252.5 有一块铁皮拱形边缘呈抛物线状, MN=4,抛
物线的顶点处到MN的距离是 4,要 在 铁皮上截
下一矩形ABCD,是矩形的顶点B、C落在 MN 上,
点A、D 落在抛物线上,问这样截下去的矩形铁
皮的周长能否等于 8,若能,求出矩形的长和宽。
若不能,说明理由。0MNABCDp再见
同课章节目录
