直线与圆、圆与圆位置关系期末复习[下学期]
文档属性
| 名称 | 直线与圆、圆与圆位置关系期末复习[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 28.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-05-29 00:00:00 | ||
图片预览



文档简介
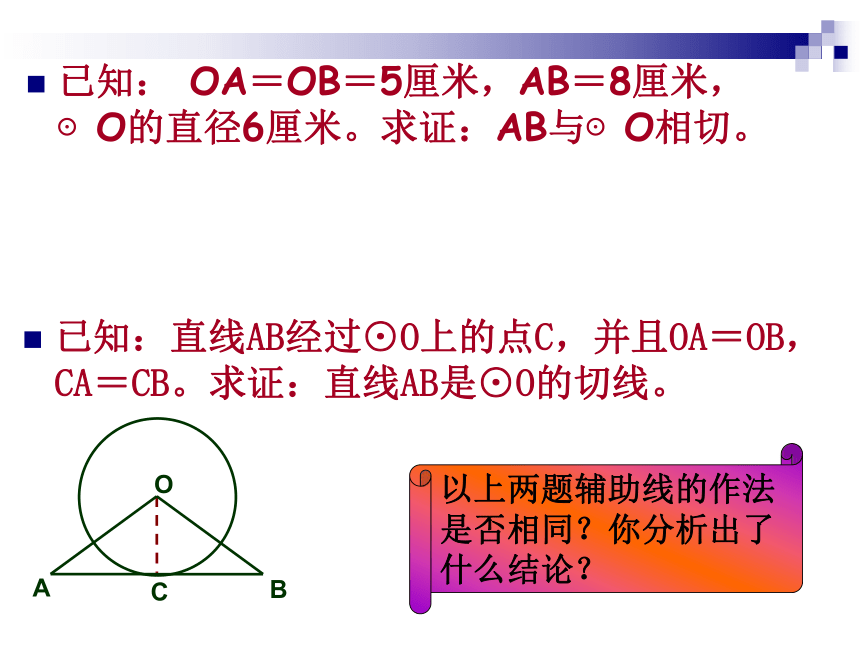
课件13张PPT。直线与圆、圆与圆的位置关系复习已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB。求证:直线AB是⊙O的切线。已知: OA=OB=5厘米,AB=8厘米,⊙O的直径6厘米。求证:AB与⊙O相切。以上两题辅助线的作法是否相同?你分析出了什么结论?证明一条直线是圆的切线,常常需要作辅助线。若直线过圆上某一点,则连结圆心和公共点,再证明直线与半径垂直若直线与圆的公共点没有确定,则过圆心向直线作垂线,再证明圆心到直线的距离等于半径。已知:AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD。
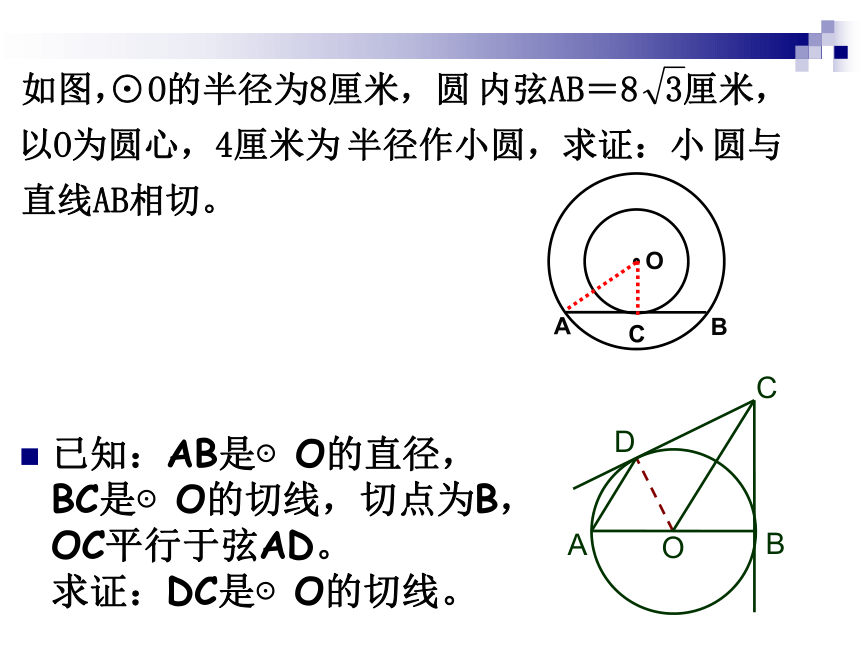
求证:DC是⊙O的切线。C如图,由正方形ABCD的顶点A引一直线分别交BD、CD及BC的延长线于E、F、G, ⊙O 是△CGF的外接圆
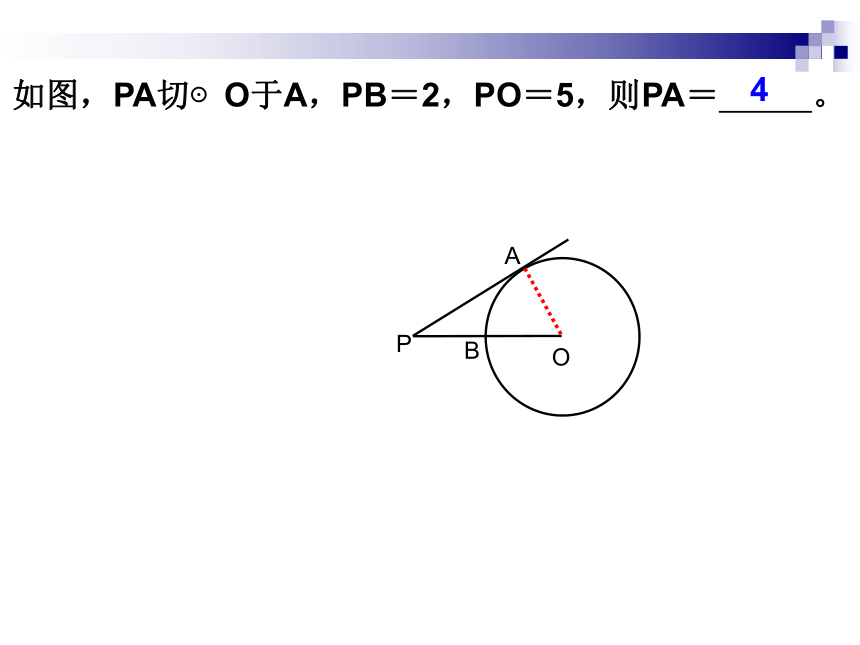
求证:CE是⊙O的切线。 如图,PA切⊙O于A,PB=2,PO=5,则PA= 。OPBA4如图,在RTΔABC中,∠C=90°,AC=3,BC=4,以BC上一点O为圆心作⊙O与AC、AB都相切,设⊙O与BC的另一个交点为D,求线段BD的长度?ACBDOE如图,在ΔABC中,AC=6,BC=8,AB=10,求ΔABC内切圆的半径.DEFO如图,在ΔABC中,AC=BC,E是内心,AE的延长线交ΔABC的外接圆于D求证:(1)BE=AEABCED1.若半径为7和9的两圆相切,则这两圆的圆心距长一定为( )
A.16 B.2 C.2或16 D.以上均不对2.若半径为1和5的两圆相交,则圆心距d的取值范围为( )
A.d<6 B. 4< d <6 C.4≤d≤6 D.1<d<53.若两圆半径为6cm和4cm,圆心距为10cm,那么这两圆的位置关系为( )
A.内切 B.相交 C.外切 D.外离CBC4.已知两圆的半径为R和r(R>r), 圆心距为d ,且
则两圆的位置关系为( )
A.外切 B. 内切 C.外离 D.外切或内切D5.两圆相切,圆心距等于3,一个圆的半径为5cm,则另一个圆的半径为 .7.两个等圆⊙O1和⊙O2相交于A,B两点, ⊙O1经过点O2,则
∠O1AB的度数为 .8.已知两圆的圆心距为5,⊙O1和⊙O2 的半径分别是方程
的两根,则两圆的关系为 .9.两圆的半径为5和3,且两圆无公共点,则两圆圆心距d的取值范围为 .2cm或8cm30°内切d>8或d<2 ⊙O1和⊙O2相切于点P,过点P的直线交于⊙O1点A,交⊙O2于点B,求证: O1A∥ O2B本题要分两种情况讨论:
一是两圆外切时,
二是两圆内切时.1如图,已知⊙O1和⊙O2相交于点A,B过点A的直线和两圆相交于C,D,过点B的直线和两圆相交E,F, 求证:DF∥CE两圆相交的问题中,公共弦是常用的辅助线
求证:CE是⊙O的切线。 如图,PA切⊙O于A,PB=2,PO=5,则PA= 。OPBA4如图,在RTΔABC中,∠C=90°,AC=3,BC=4,以BC上一点O为圆心作⊙O与AC、AB都相切,设⊙O与BC的另一个交点为D,求线段BD的长度?ACBDOE如图,在ΔABC中,AC=6,BC=8,AB=10,求ΔABC内切圆的半径.DEFO如图,在ΔABC中,AC=BC,E是内心,AE的延长线交ΔABC的外接圆于D求证:(1)BE=AEABCED1.若半径为7和9的两圆相切,则这两圆的圆心距长一定为( )
A.16 B.2 C.2或16 D.以上均不对2.若半径为1和5的两圆相交,则圆心距d的取值范围为( )
A.d<6 B. 4< d <6 C.4≤d≤6 D.1<d<53.若两圆半径为6cm和4cm,圆心距为10cm,那么这两圆的位置关系为( )
A.内切 B.相交 C.外切 D.外离CBC4.已知两圆的半径为R和r(R>r), 圆心距为d ,且
则两圆的位置关系为( )
A.外切 B. 内切 C.外离 D.外切或内切D5.两圆相切,圆心距等于3,一个圆的半径为5cm,则另一个圆的半径为 .7.两个等圆⊙O1和⊙O2相交于A,B两点, ⊙O1经过点O2,则
∠O1AB的度数为 .8.已知两圆的圆心距为5,⊙O1和⊙O2 的半径分别是方程
的两根,则两圆的关系为 .9.两圆的半径为5和3,且两圆无公共点,则两圆圆心距d的取值范围为 .2cm或8cm30°内切d>8或d<2 ⊙O1和⊙O2相切于点P,过点P的直线交于⊙O1点A,交⊙O2于点B,求证: O1A∥ O2B本题要分两种情况讨论:
一是两圆外切时,
二是两圆内切时.1如图,已知⊙O1和⊙O2相交于点A,B过点A的直线和两圆相交于C,D,过点B的直线和两圆相交E,F, 求证:DF∥CE两圆相交的问题中,公共弦是常用的辅助线
