浙教版数学八上1.5三角形全等的判定SSS 同步学案(无答案)
文档属性
| 名称 | 浙教版数学八上1.5三角形全等的判定SSS 同步学案(无答案) | 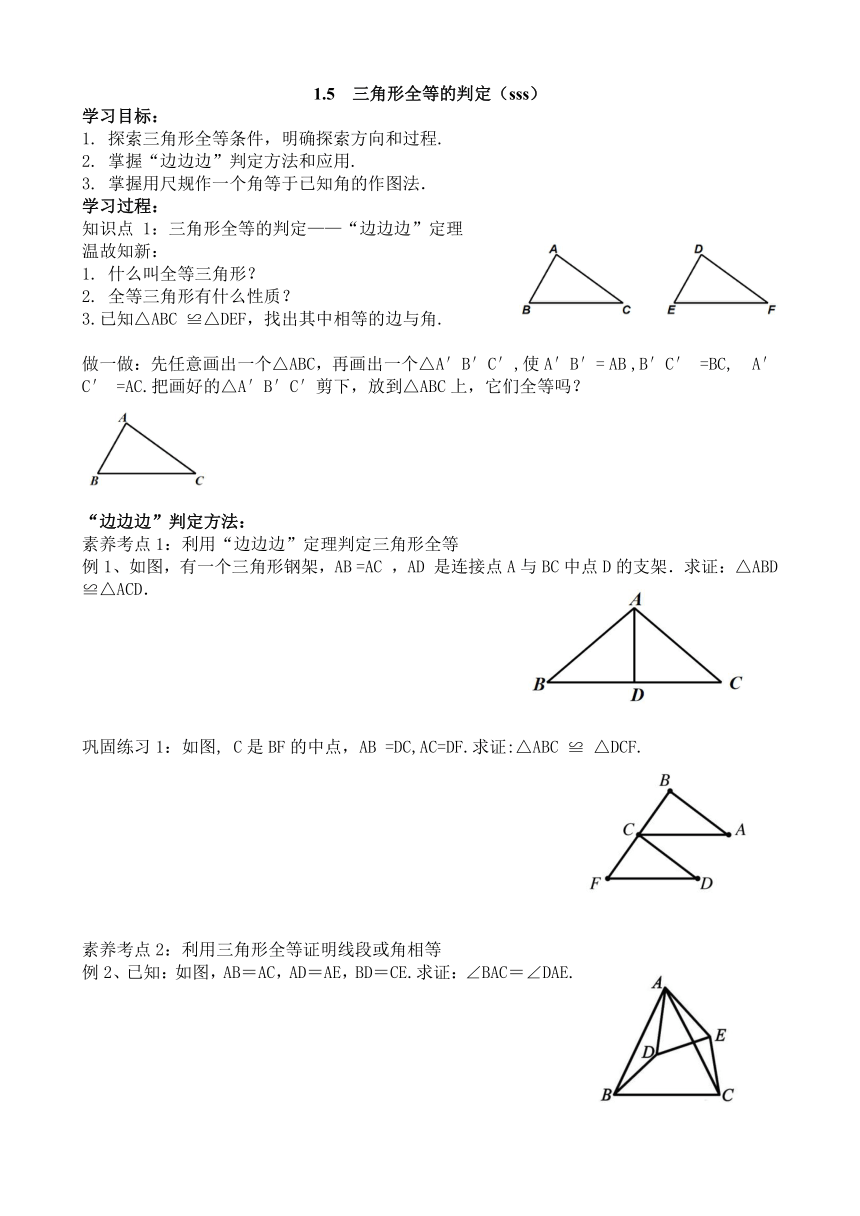 | |
| 格式 | zip | ||
| 文件大小 | 174.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-30 18:40:59 | ||
图片预览

文档简介
1.5 三角形全等的判定(sss)
学习目标:
1. 探索三角形全等条件,明确探索方向和过程.
2. 掌握“边边边”判定方法和应用.
3. 掌握用尺规作一个角等于已知角的作图法.
学习过程:
知识点 1:三角形全等的判定——“边边边”定理
温故知新:
什么叫全等三角形?
2. 全等三角形有什么性质?
3.已知△ABC ≌△DEF,找出其中相等的边与角.
做一做:先任意画出一个△ABC,再画出一个△A′B′C′,使A′B′= AB ,B′C′ =BC, A′ C′ =AC.把画好的△A′B′C′剪下,放到△ABC上,它们全等吗?
“边边边”判定方法:
素养考点1:利用“边边边”定理判定三角形全等
例1、如图,有一个三角形钢架,AB =AC ,AD 是连接点A与BC中点D的支架.求证:△ABD ≌△ACD.
巩固练习1:如图, C是BF的中点,AB =DC,AC=DF.求证:△ABC ≌ △DCF.
素养考点2:利用三角形全等证明线段或角相等
例2、已知:如图,AB=AC,AD=AE,BD=CE.求证:∠BAC=∠DAE.
巩固练习2:教材的对应练习
知识点 2:用尺规作一个角等于已知角
例3 :用尺规作一个角等于已知角.已知:∠AOB.求作: ∠A′O′B′=∠AOB.
巩固练习3: 已知:∠AOB.求作:∠A'O'B',使∠A'O′B'=∠AOB,
(1)如图1,以点O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;
(2)如图2,画一条射线O′A′,以点O′为圆心,OC长为半径作弧,交O′A′于点C′;
(3)以点C′为圆心,CD长为半径画弧,与第2步中所画的弧交于点D′;
(4)过点D′画射线O′B',则∠A'O'B'=∠AOB.
根据以上作图步骤,
请你证明∠A'O'B′=∠AOB.
当堂检测:
1. 如图,D,F是线段BC上的两点,AB=EC,AF=ED, 要使△ABF≌△ECD ,还需要条件_________ (填一个条件即可).
2.如图,AB=CD,AD=BC, 则下列结论: ①△ABC≌△CDB; ②△ABC≌△CDA;③△ABD ≌△CDB;④ BA∥DC.正确的个数是 ( )
A . 1个 B. 2个
C. 3个 D. 4个
3.如图,EF=BC,DF=AC,DA=EB.求证∠F=∠C.
4.已知:如图,点A,D,C,B在同一条直线上,AD=BC,AE=BF,CE=DF,求证:AE∥BF.
5.已知:如图,AB=AE,AC=AD,BD=CE,求证:△ABC ≌△AED.
6. 如图,AD=BC,AC=BD.求证:∠C=∠D .(提示: 连结AB)
学习目标:
1. 探索三角形全等条件,明确探索方向和过程.
2. 掌握“边边边”判定方法和应用.
3. 掌握用尺规作一个角等于已知角的作图法.
学习过程:
知识点 1:三角形全等的判定——“边边边”定理
温故知新:
什么叫全等三角形?
2. 全等三角形有什么性质?
3.已知△ABC ≌△DEF,找出其中相等的边与角.
做一做:先任意画出一个△ABC,再画出一个△A′B′C′,使A′B′= AB ,B′C′ =BC, A′ C′ =AC.把画好的△A′B′C′剪下,放到△ABC上,它们全等吗?
“边边边”判定方法:
素养考点1:利用“边边边”定理判定三角形全等
例1、如图,有一个三角形钢架,AB =AC ,AD 是连接点A与BC中点D的支架.求证:△ABD ≌△ACD.
巩固练习1:如图, C是BF的中点,AB =DC,AC=DF.求证:△ABC ≌ △DCF.
素养考点2:利用三角形全等证明线段或角相等
例2、已知:如图,AB=AC,AD=AE,BD=CE.求证:∠BAC=∠DAE.
巩固练习2:教材的对应练习
知识点 2:用尺规作一个角等于已知角
例3 :用尺规作一个角等于已知角.已知:∠AOB.求作: ∠A′O′B′=∠AOB.
巩固练习3: 已知:∠AOB.求作:∠A'O'B',使∠A'O′B'=∠AOB,
(1)如图1,以点O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;
(2)如图2,画一条射线O′A′,以点O′为圆心,OC长为半径作弧,交O′A′于点C′;
(3)以点C′为圆心,CD长为半径画弧,与第2步中所画的弧交于点D′;
(4)过点D′画射线O′B',则∠A'O'B'=∠AOB.
根据以上作图步骤,
请你证明∠A'O'B′=∠AOB.
当堂检测:
1. 如图,D,F是线段BC上的两点,AB=EC,AF=ED, 要使△ABF≌△ECD ,还需要条件_________ (填一个条件即可).
2.如图,AB=CD,AD=BC, 则下列结论: ①△ABC≌△CDB; ②△ABC≌△CDA;③△ABD ≌△CDB;④ BA∥DC.正确的个数是 ( )
A . 1个 B. 2个
C. 3个 D. 4个
3.如图,EF=BC,DF=AC,DA=EB.求证∠F=∠C.
4.已知:如图,点A,D,C,B在同一条直线上,AD=BC,AE=BF,CE=DF,求证:AE∥BF.
5.已知:如图,AB=AE,AC=AD,BD=CE,求证:△ABC ≌△AED.
6. 如图,AD=BC,AC=BD.求证:∠C=∠D .(提示: 连结AB)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
