2.3有理数的乘法1

课件19张PPT。欢迎指导！有理数的乘法（一）问题探究如果记蜗牛向右爬行为正，则向左爬行2cm应记作什么？－2cm问题探究 一只蜗牛沿直线l爬行，它现在的位置恰在l上的点O。(规定向右为正)回答下列问题：
(1)如果蜗牛一直以每分2cm的速度向右爬行，3分钟后它在什么位置？结果：应在O点的右边6cm处。
列式： （＋２）×（＋３） ＝＋６(2)如果蜗牛一直以每分2cm的速度向左爬行，3分钟后它在什么位置？结果：应在O点的左边6cm处。
列式： （－２）×（＋３） ＝－６ 一只蜗牛沿直线l爬行，它现在的位置
恰在l上的点O。(规定向右为正)回答下列
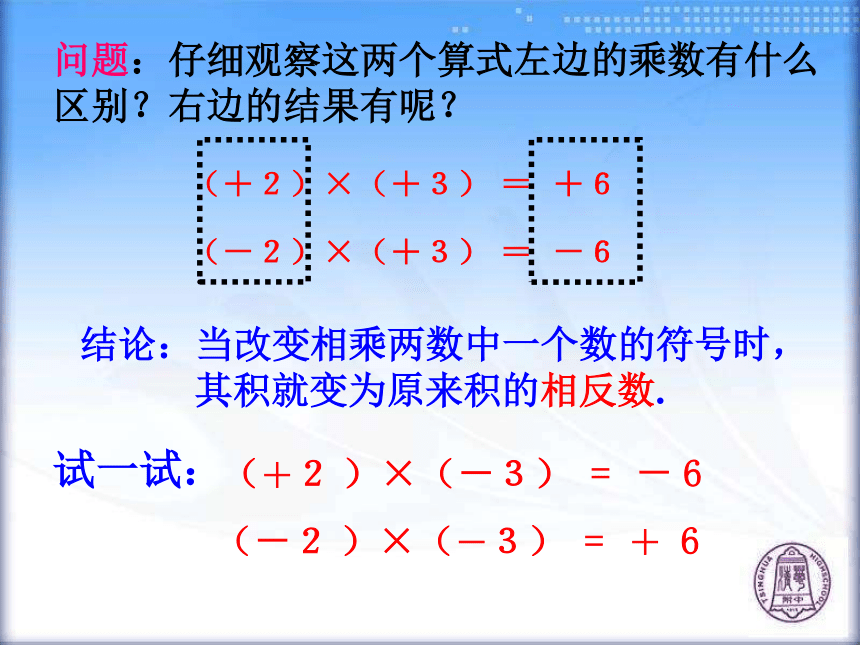
问题：问题探究（＋２）×（＋３） ＝ ＋６（－２）×（＋３） ＝ －６问题：仔细观察这两个算式左边的乘数有什么
区别？右边的结果有呢？试一试：（＋２ ）×（－３） = （－２ ）×（－３） = － 6
＋ 6
结论：当改变相乘两数中一个数的符号时，
其积就变为原来积的相反数.（＋２）×（＋３） = ＋ 6（－２ ）×（＋３） = － 6探究新知请同学们观察上述出现的四个式子，思考下列问题：(2)积的绝对值与这两个乘数的绝对值有什么关系？（＋２ ）×（－３） = － 6（－２ ）×（－３） = ＋ 6(1)两数相乘时，积的符号与这两个数的符号有什么关系？综合如下：
（1）（+2）×（+3）= + 6
（2）（-2）×（-3）= + 6
（3）（-2）×（+3）= - 6
（4）（+2）×（-3）= - 6
（5）任何数同0相乘同号异号绝对值相乘两数相乘，同号得正，异号得负，并把绝对值相乘；
任何数同0相乘，都得0。探究新知都得0有理数乘法法则:得正得负1、 2×（ － 3）
2、（ － 3）× （ － 2）
3、（ + 4） × （ － 5）
4、（ + 2.5） × （ + 4）
快速回答：说出下列算式的符号, 并说明理由.－＋－＋例1 计算： (3) ( -2.5 ) × 4 (2)运算中的
第一步是
______________。第二步是
______________。先确定积的符号 再把绝对值相乘探究新知注意:0没有倒数。 若两个有理数乘积为1，
就称这两个有理数互为倒数。知识运用练一练：求下列数的倒数1-71和-1计算：
（1）（-1）×2×3×4=
（2）（-1）×（-2）×3×4=
（3）（-1）×（-2）×（-3）×4=
（4）（-1）×（-2）×（-3）×（-4）=
（5）（-1）×（-2）×（-3）×（-4）×0=－24＋24－24＋240多个不为零的有理数相乘，积的符号怎样确定呢？ 多个不为零的有理数相乘，积的符号由 确定：负因数的个数负因数的个数为偶数时，则积为正;
负因数的个数为奇数时，则积为负; 几个有理数相乘,当有一个因数为 0 时，积为0 。例 题 解 析例2 计算：
(1) (?4)×5×(?0.5)

(2)
(3)(4)说一说这节课的收获！小结：1.有理数乘法法则：两数相乘,同号得正,异号得负,并把绝对值相乘,任何数同0相乘,都得0。2.如何进行两个（多个）有理数的运算：先确定积的符号，再把绝对值相乘，当有一个因数为零时，积为零。
分层作业：
1、基础性作业：课本P41 A组 作业本
2、巩固性作业：课本P42 B组
挑战自我用“＞” “＜” “＝”号填空.(1)（ -4）×(-7 ) 0 (4)（+ 7）×(－ ) （-7）×（- ）＜＞＝(2)（ -5）×(+4) 0＜试一试：