矩形的判定教学设计

《矩形的判定》 教学设计
陕西省延安富县沙梁中学——钞晓东
一、教学目标
知识与技能目标
⑴、理解并掌握矩形的判定方法。
⑵、使学生能应用矩形的定义、判定等知识，解决简单的证明题和计算题，进一步培养学生的分析能力。
过程与方法目标
经历探索矩形判定的过程，发展学生实验探索的意识；形成几何分析思路和方法。
情感态度价值观目标
培养推理能力，会根据需要选择有关的结论证明，体会来自于实践的需要。
二、教学重点与难点
重点：矩形的判定的内容。
难点：矩形判定定理的证明以及灵活应用。
三、教学手段方法：
多媒体直观演示与几何论证相结合，由易到难、层层深入的探究式教学方法进行教学。
四、教学过程
1、教学流程设计
2、教学过程设计
问题与情境 师生互动行为 设计意图
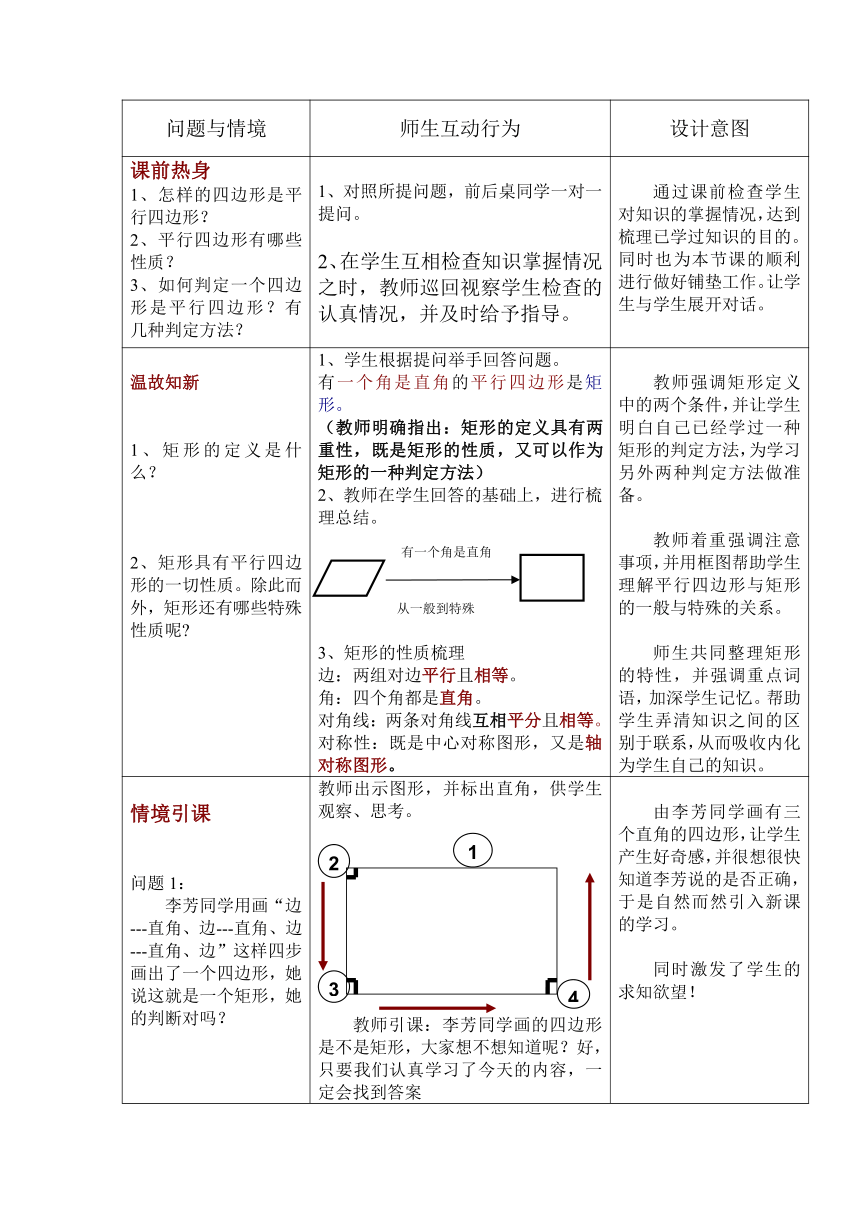
课前热身1、怎样的四边形是平行四边形？2、平行四边形有哪些性质？3、如何判定一个四边形是平行四边形？有几种判定方法？ 1、对照所提问题，前后桌同学一对一提问。2、在学生互相检查知识掌握情况之时，教师巡回视察学生检查的认真情况，并及时给予指导。 通过课前检查学生对知识的掌握情况，达到梳理已学过知识的目的。同时也为本节课的顺利进行做好铺垫工作。让学生与学生展开对话。
温故知新1、矩形的定义是什么？2、矩形具有平行四边形的一切性质。除此而外，矩形还有哪些特殊性质呢 1、学生根据提问举手回答问题。有一个角是直角的平行四边形是矩形。（教师明确指出：矩形的定义具有两重性，既是矩形的性质，又可以作为矩形的一种判定方法）2、教师在学生回答的基础上，进行梳理总结。3、矩形的性质梳理边：两组对边平行且相等。角：四个角都是直角。对角线：两条对角线互相平分且相等。对称性：既是中心对称图形，又是轴对称图形。 教师强调矩形定义中的两个条件，并让学生明白自己已经学过一种矩形的判定方法，为学习另外两种判定方法做准备。 教师着重强调注意事项，并用框图帮助学生理解平行四边形与矩形的一般与特殊的关系。师生共同整理矩形的特性，并强调重点词语，加深学生记忆。帮助学生弄清知识之间的区别于联系，从而吸收内化为学生自己的知识。
情境引课问题1：李芳同学用画“边---直角、边---直角、边---直角、边”这样四步画出了一个四边形，她说这就是一个矩形，她的判断对吗？ 教师出示图形，并标出直角，供学生观察、思考。教师引课：李芳同学画的四边形是不是矩形，大家想不想知道呢？好，只要我们认真学习了今天的内容，一定会找到答案下面，让我们共同学习探究《矩形的判定》 由李芳同学画有三个直角的四边形，让学生产生好奇感，并很想很快知道李芳说的是否正确，于是自然而然引入新课的学习。 同时激发了学生的求知欲望！
探究新知一、从“角”的角度探究思考;1、有一个角是直角的 四边形一定是矩形吗？2、有两个角是直角的四边形一定是矩形吗？3、有三个角是直角的 四边形一定是矩形吗？二、从“对角线”的角度探究问题2：木工师傅用皮尺度量窗户的对角线的长是否相等，以确保图形是矩形。你想知道其中的道理吗？思考2(1)对角线相等的四边形是矩形吗 (2) 对角线相等的平行四边形是矩形吗 课后练习第一题：为庆祝“十一”国庆节，八（13）班的同学要在广场布置一个矩形的花坛。计划用串红摆成两条对角线，如果一条对角线用了38盆花，还需搬来多少盆“串红”？如果一条对角线用了49盆呢？为什么？ 教师提问：1、矩形的边相对于平行四边形有特殊性质吗？没有。那我们从角的角度来探究“最少有几个直角的四边形”是矩形。2、以上问题：如果是，说明理由，如果不是，请举出反例。3、指名板演，画出反例图形。由图可知，1和2都不是矩形。4、猜想：有三个角是直角的 四边形是矩形。李芳同学画的四边形很可能是矩形。你会证明吗？教师出示命题：“有三个角是直角的四边形是矩形”5、如何证明一个文字命题呢？教师叙述一般过程：第一：根据题意，画出图形。第二：分清命题的题设和结论，结合图形，写出已知和求证。第三：写出证明过程（有时需要写依据）。第四：归纳结论。学生说出已知和求证，并尝试证明。6、通过证明发现我们的猜想是正确的，李芳的画法也是正确的。所以，我们把“有三个角是直角的四边形是矩形”作为矩形的判定定理1。7、那么，有四个角的四边形是矩形吗？再有必要这样说吗？1、师提问：矩形的对角线相对于平行四边形也具有其特殊性，那么，(1)对角线相等的四边形是矩形吗 (2) 对角线相等的平行四边形是矩形吗 如果是，说明理由；如果不是，举出反例。（小组讨论）第一题：学生画的反例：不是矩形。第二题图：学生猜想。2、请你用与上面相同的格式把文字命题转化为数学语言，并尝试证明。得出结论：“对角线相等的平行四边形是矩形”。作为矩形的判定定理2。3、判断木工师傅的做法是否合理？ 首先，让学生明确，矩形的边与平行四边形的的边具有相同的性质，所以，无需从边的角度探讨矩形的判定方法。其次，由李芳画角的方法，引出了，从角的角度探究“最少有几个直角的四边形是矩形”。于是，学生会从最少一个开始探究。易于引起学生的探究热情。鼓励学生逐步深入探究，发展实验探索意识和锲而不舍的探索精神。教师强调：证明文字命题的的基本格式，目的在于，让学生养成规范证明的习惯，认识到数学基本功要靠平时锻炼。一定要重视 “数学基本功”。从对角线的角度出发，运用矩形的前两个判定方法判定“对角线相等的平行四边形是矩形”。让学生通过证明，理解掌握矩形的第三种判定方法。通过小组讨论交流，发现问题，得出猜想。再通过学生自己证明，培养学生分析几何问题的能力和严密的逻辑推理能力。练习题1图示 1、偶数盆花2、奇数盆花
归纳新知目前，我们已经学习了矩形的几种判定方法？ 学生口述，教师用几何语言出示：1、定义判定法 ∵在 ABCD中,∠A=90°∴ ABCD是矩形。2、判定定理1∵在四边形ABCD中，∠A=∠B=∠C=90°∴ 四边形 ABCD是矩形。3、判定定理2 ∵在 ABCD中, AC=BD ∴ ABCD是矩形。 梳理矩形的三种判定方法，意在让学生理解掌握它们逻辑严密的推理过程。并能灵活运用每一种判定方法，解决实际问题。
检查双基：判断对错，并说明理由或举出反例：⒈对角线相等的四边形是矩形（ × ）⒉对角线互相平分且相等的四边形是矩形（ √ ）⒊有一个角是直角的四边形是矩形（ × ）⒋四个角都相等的四边形是矩形（ √ ）⒌对角线相等,且有一个角是直角的四边形是矩形（ × ）⒍一组邻边垂直，一组对边平行且相等的四边形是矩形（ √ ）⒎对角线相等且互相垂直的四边形是矩形（ × ） 1、教师出示判断题，强调学习要求。通过小组讨论完成。具体做法，前排学生与后一排学生组成四人小组进行讨论，然后选派代表发言。2、学生按要求进行讨论，教师巡回检查指导，发现问题及时纠正。3、鼓励学生，动手实践，画出反例图形，从而做出正确的判断。4教师适当点拨，第6、8小题，指导学生按要求、按条件画图。5、教师画出第6、第8题的反例图形，让学生观察，然后做出判断。 第5题 第7题 本环节放手让学生之间合作学习，互相交流，交换观点，自主构建知识体系，能灵活运用所学知识进行正确判断，给学生自主学习交流提供空间。同时，通过交流让学生用自己的语言清楚表达解决问题的过程，可以培养学生语言表达能力和积极发言的胆略。体现开放性原则、过程性原则性教学原则。
解决问题例1：已知M为 ABCD的AD边的中点，且MB＝MC。 求证： ABCD是矩形变式训练一：把例1中的的条件“MB=MC”换成“∠MBC=∠MCB”结论还成立吗？变式训练二：已知，如图，在四边形ABCD中，AB=CD,∠B=∠D=90°求证：四边形ABCD是矩形。 1、教师组织学生熟悉题意后，指名说话证明思路，其余学生判断正误。2、教师出示证明过程让学生对照检查，并强调证明过程的逻辑性和严密性，注意书写格式。证明：∵ABCD是平行四边形∴ ∠A＋ ∠D＝180°AB＝DC∵M是AD的中点∴AM＝DM∵ MB＝MC∴△BAM≌ △CDM∴∠A＝ ∠D∴∠A＝ 90°∴ ABCD是矩形。学生口述证明过程，教师与其余学生共同评判。3、变式训练二，教师提问后，稍加点拨后，学生代表发表意见，教师适当提示和鼓励。 14、教师提问：你有几种证法？学生独立完成，教师检查完成情况。给予及时评价。 1、通过学生回答证明过程，培养学生数学推理能力和思维能力。培养学生良好的数学素养和品质。2、通过便是训练，培养学生思维的灵活性和创造性。变式训练一利用“同一三角形中，等角对等边”可以转化为例1的条件，从而得以证明。变式训练二，教师适当点播，引导学生作辅助线：连接对角线AC,可以构建全等三角形，从而达到证明四边形ABCD是矩形的目的。
反思与评价问题：请同学们对照以下三个问题进行评价和反思：1、我今天收获了哪些知识、方法？2、我还有哪些困惑？3、我的自我评价或评价他人、集体或老师。思考与延伸平行四边形平移一条较短边，使得平行四边形的一组邻边相等，得到的又是怎样的特殊四边形呢？它有何性质呢？（预习） 教师强调：遇到具体题目，可根据条件灵活选用适当的方法。教师用框图进一步说明矩形的判定方法以及之间的关系。教师评价同学：布置作业：19.2 第一题和第二题。课后思考与延伸：出示第一题、第二题（预习下节课） 在学生谈收获的基础上，教师梳理知识体系，帮助学生理清知识层次，掌握重点内容，为今后学习打好基础。1、矩形的判定方法的前提基础有两种：①从四边形来判定；②从平行四边形来判定。2、常用的判定矩形的方法有三种：①定义判定法，②判定定理1③判定定理2。通过学生评价和和反思，理清知识结构，掌握本节课的重点内容，即：矩形的三种判定方法。体验克服困难的过程，树立良好的自信心。最后一个环节，让学生为学习下一课时《菱形》做准备。
板书设计由于板书内容的存留性，加深学生记忆和巩固新知。重点内容板书于黑板，帮助学生回顾全课，整理知识。 19.2.1 矩形的判定 1、 定义：∵在 ABCD中,∠A=90°∴ ABCD是矩形。2、判定定理1矩形的判定 ∵在四边形ABCD中，∠A=∠B=∠C=90°∴ 四边形 ABCD是矩形。3、判定定理2 ∵在 ABCD中, AC=BD ∴ ABCD是矩形。例题解答过程（略） 学生画反例图形
温故知新
归纳结论
探究新知
情境引课
课堂巩固
解决问题
思考与延伸
反思与评价
有一个角是直角
从一般到特殊
1
2
3
4
A
B
D
C
M
A
D
1
B
C
小结
有一个角是直角
对角线相等
有三个角是直角
平行四边形
矩形
四边形