有理数的乘方[上学期]

2.5有理数的乘方（1）
1、 教材分析
在古代我们就有《棋盘上的学问》的故事，这一故事早已接涉及到了乘方
这一运算。乘方运算是一种有理数新的运算，它构成了有理数的三级运算，在以后的学习中我们还将广泛的使用乘方的知识，如科学记数法，泰勒展式等内容。
2、 学习类型与任务分析
（1） 学习类型
1、 学习结果
（1）乘方、幂、指数、底数的概念是数学概念。
（2）乘方的符号表示“an”是数学事实。
（3）幂的符号法则是数学原理。
（4）通过实例经历乘方概念产生的过程及例题的分析过程是数学认识策
略。
（5）进行乘方、乘、除的简单混合计算是数学问题解决。
（6）把有理数的乘方转化为求几个相同有理数的乘法运算是数学技能，数学思想方法。
（二）学习形式
由于有理数的乘法运算及求几个相同因式的乘法运算与有理数的乘方的知识构成了类属关系，即下位关系，因此本课时采用上位学习。
（三）学习任务分析
有理数的乘方
负数相乘的符号法则
乘方的概念 有理数乘方混合运算 幂的符号法则 负数相乘的符号法则
0
底数 幂 指数 几个相同有理数的乘法 有理数的除法法则
3、 学生的起点能力
（1） 会计算给定边长的正方形的面积及给定棱长的正方体的体积。
（2） 理解有理数的概念，清楚我们所讨论的运算的数域是有理数域。
（3） 有理数乘法的法则，会计算求几个相同有理数的乘法。
（4） 掌握了几个不等于0的有理数相乘所得的积的符号法则。
（5） 会计算有理数的除法。
4、 教学目标
1、 使学生理解乘方、幂、底数、指数的概念，了解乘方概念产生的过程。
2、 掌握乘方与幂的表示法，理解幂的符号法则。
3、 理解相同因数的乘方与乘法的互相转化，掌握有理数的乘方运算以及
乘方、乘、除混合运算。
5、 教学重、难点
重点：乘方的概念、运算。
难点：幂、底数、指数、乘方的概念及乘方、乘、除的混合运算。
6、 教学步骤
教学步骤 教师活动 学生活动 设计意图
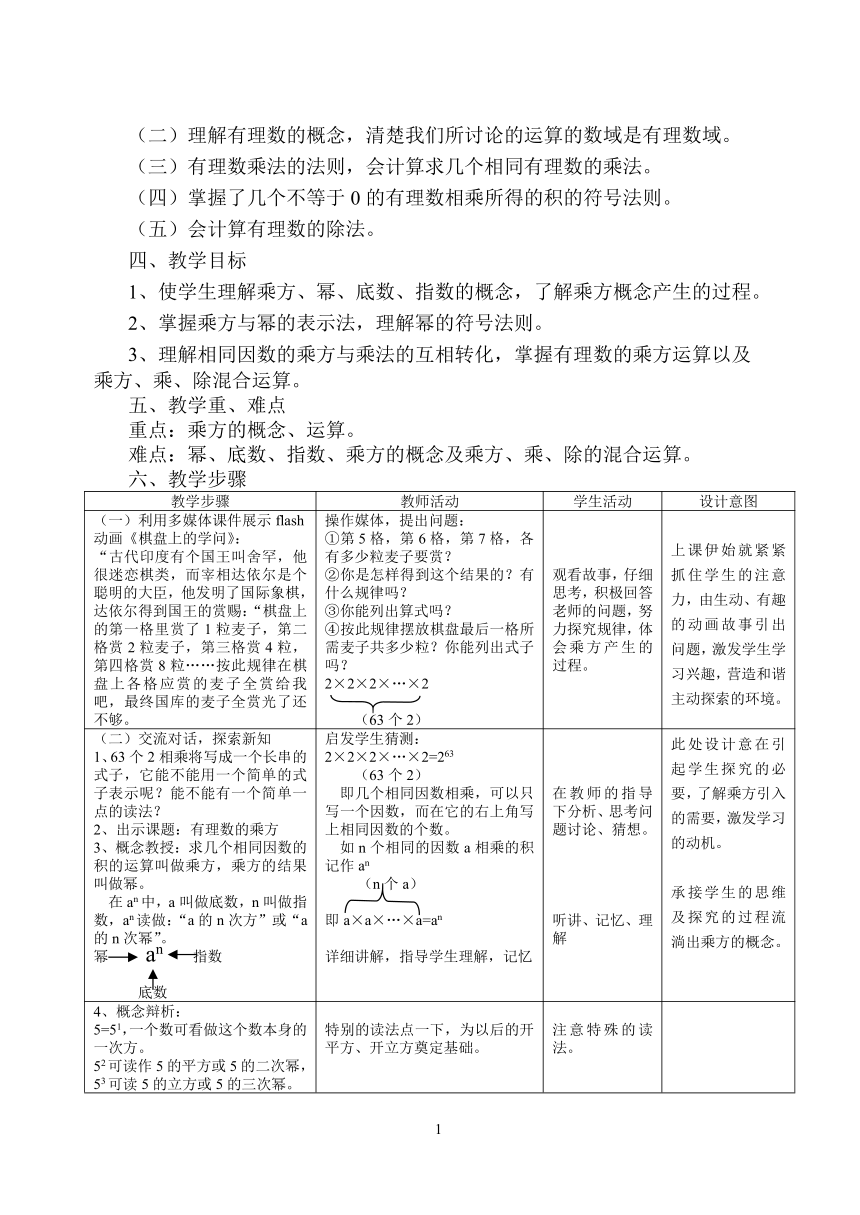
（一）利用多媒体课件展示flash动画《棋盘上的学问》：“古代印度有个国王叫舍罕，他很迷恋棋类，而宰相达依尔是个聪明的大臣，他发明了国际象棋，达依尔得到国王的赏赐：“棋盘上的第一格里赏了1粒麦子，第二格赏2粒麦子，第三格赏4粒，第四格赏8粒……按此规律在棋盘上各格应赏的麦子全赏给我吧，最终国库的麦子全赏光了还不够。 操作媒体，提出问题：①第5格，第6格，第7格，各有多少粒麦子要赏？②你是怎样得到这个结果的？有什么规律吗？③你能列出算式吗？④按此规律摆放棋盘最后一格所需麦子共多少粒？你能列出式子吗？2×2×2×…×2 （63个2） 观看故事，仔细思考，积极回答老师的问题，努力探究规律，体会乘方产生的过程。 上课伊始就紧紧抓住学生的注意力，由生动、有趣的动画故事引出问题，激发学生学习兴趣，营造和谐主动探索的环境。
（二）交流对话，探索新知1、63个2相乘将写成一个长串的式子，它能不能用一个简单的式子表示呢？能不能有一个简单一点的读法？2、出示课题：有理数的乘方3、概念教授：求几个相同因数的积的运算叫做乘方，乘方的结果叫做幂。在an中，a叫做底数，n叫做指数，an读做：“a的n次方”或“a的n次幂”。幂 an 指数 底数 启发学生猜测：2×2×2×…×2=263（63个2）即几个相同因数相乘，可以只写一个因数，而在它的右上角写上相同因数的个数。如n个相同的因数a相乘的积记作an（n个a）即a×a×…×a=an详细讲解，指导学生理解，记忆 在教师的指导下分析、思考问题讨论、猜想。听讲、记忆、理解 此处设计意在引起学生探究的必要，了解乘方引入的需要，激发学习的动机。承接学生的思维及探究的过程流淌出乘方的概念。
4、概念辩析：5=51，一个数可看做这个数本身的一次方。52可读作5的平方或5的二次幂，53可读5的立方或5的三次幂。（1）把下列各式写成幂的形式并说出指数、底数和读法（-2）（-2）（-2）（-2）=1.5×1.5×1.5×1.5=3/4×3/4×3/4×3/4×3/4=（2）反过来成立吗？（-2）4=（3）说一说：25，52，5×2有可区别？ 特别的读法点一下，为以后的开平方、开立方奠定基础。教师巡回指导提出问题，评价学生解答，及时纠正学生错误，加深对概念的理解。注意：幂的底数是分数或负数时，底数应添上括号（－2）4，（3/4）5等。 注意特殊的读法。个别学习思考回答问题，深刻理解有关概念，并重视教师强调的注意点。 加深对概念的理解，强调注意点。
（三）应用新知，体验成功1、P49例1讲解（1）（－3）2 （2）1.53（3）（－4/3）4 （4）（－1）11解：（1）（－3）2=（－3）×（－3）=9（2）1.53=1.5×1.5×1.5=3.375（3）（－4/3）4=（-4/3）×（-4/3）×（-4/3）×（-4/3）=256/81（4）（－1）11＝－1 计算时注意提醒学生先把要求的式子写成几个有理数相等的形式，转化成有理数的乘法计算，底数是带分数的要化成假分数。可先定号再计算绝对值。 听讲、思考、计算 此环节重在运用新知，体验新知识的应用，并检查对新知识理解。
2、a 观察例1中式子（1）（3）（4）及（2）猜测有理数幂的符号法则幂的符号法则：（1）正数的任何次幂都是正数，负数的奇次幂是负数，负数的偶次幂是正数。（2）1的任何次幂都是1，－1的偶次幂都是1，－1的奇次幂都是－1。（3）零的任何次幂都是零。 启发诱导，层层设问，探究规律评价 归纳 在教师的指导下积极思考，尝试归纳、小组讨论、交流 使学生学会乘方的算法，依据概念计算再次巩固乘方的有关概念。
2、P48例2讲解计算：（1）－32（2）3×23（3）（3×2）3（4）8÷（－2）3解：（1）－32＝－（3×3）＝－9（2）3×23＝3×8＝24（3）（3×2）3＝63＝216（4）8÷（－2）3＝8÷（－8）＝－1 讲评时要先让学生分清每一题中有哪几种运算，然后按顺序：先算乘方，再算乘除，有括号的先算括号里的。 个别学习，动手演算 掌握有理数乘、除、乘方的混合运算。
3、P48，课内练习 巡回指导 个别学习上黑板演算 检验掌握程度
（四）课堂小结（与学生一起归纳）（1）有理数乘方的概念（2）幂的符号法则（3）乘、除、乘方的混合运算…… 指导学生小结、归纳，最后在学生的基础上概括。 回顾知识，举手回答，概括归纳。 使学生回顾所学知识，明确学习要求及重点。
（五）布置作业作业本2.5有理的乘方、课本A组题1.回顾：边长为5的正方形的面积=5×5=52=25棱长为5 的正方体的体积=5×5×5=53=1252、
PAGE
1