2.7探索勾股定理(一)教学设计
图片预览

文档简介
探索勾股定理(一)
一、学情分析
学生经历了一年的初中学习,具备了一定的归纳、总结、类比、转化以及数学表达的能力,对现实生活中的数学知识充满了强烈的好奇心与探究欲,并能在老师的指导下通过小组成员间的互助合作,发表自己的见解。另外,在学本节课时,通过前置知识的学习,学生对直角三角形有了初步的认识,并能从直观把握直角三角形的一些特征,为此在授课时要抓住学生的这些特点,激发学生学习数学的兴趣,建立他们的自信心,为学生空间观念的发展、数学活动经验的积累、个性的发挥提供机会。
二、教材分析
(一)本节内容分析
本节课是勾股定理的第1课时,根据课程标准的要求,注意让学生经历探索勾股定理的过程,鼓励学生用不同的方法解决问题,在解决问题的过程中,注意渗透数形结合的思想。另外,勾股定理具有很高的文化价值,这点要充分体现,以提高学生探索的欲望。
(二)教学目标
1、经历探索勾股定理的过程,提高学生的推理能力,体会数形结合的思想。
2、理解并掌握勾股定理。
3、通过对勾股定理的历史介绍及交流,让学生体会它的文化价值,提高学习数学的兴趣和信心。
(三)教学重难点
1、教学重点:掌握勾股定理,让学生深刻感悟到直角三角形三边所具备的特殊关系。
2、教学难点:勾股定理的证明
三、教学设计
教学环节 教 师 活 动 学 生 活 动
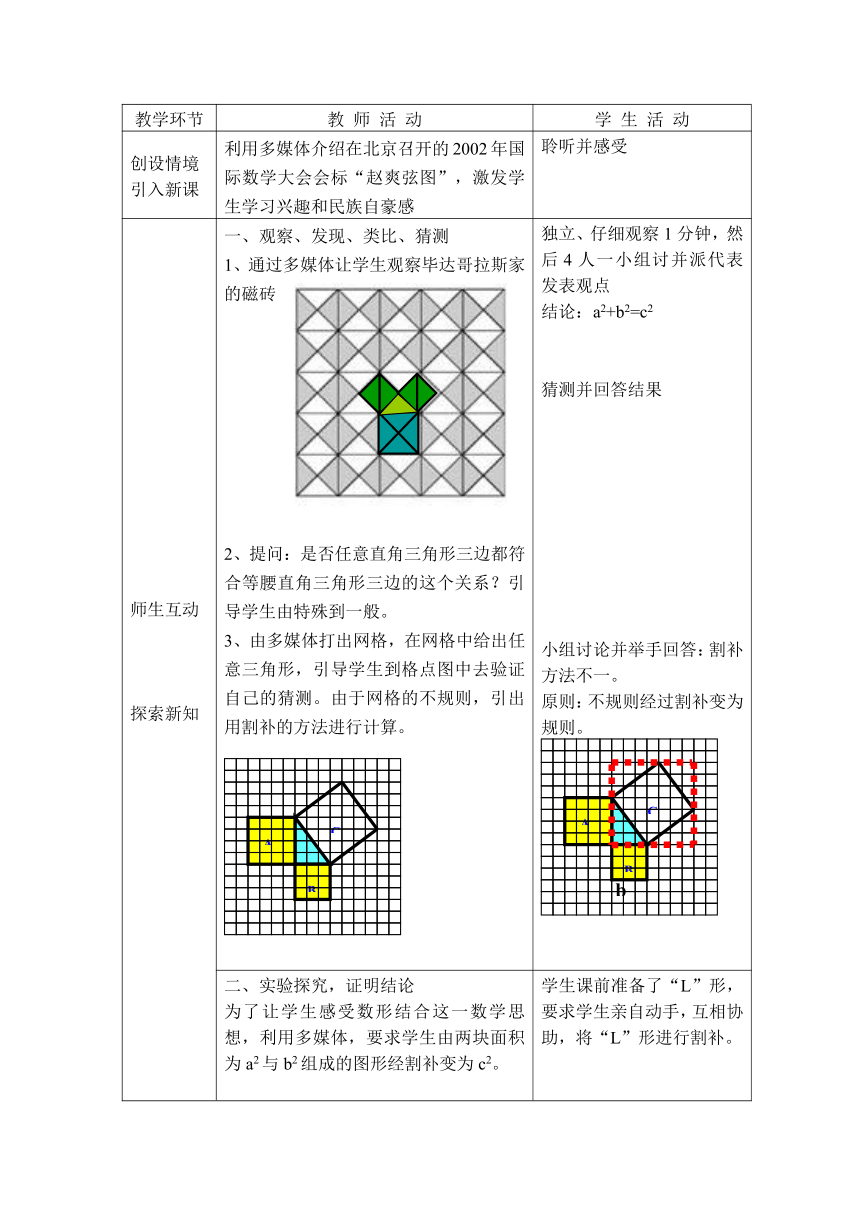
创设情境引入新课 利用多媒体介绍在北京召开的2002年国际数学大会会标“赵爽弦图”,激发学生学习兴趣和民族自豪感 聆听并感受
师生互动探索新知 一、观察、发现、类比、猜测1、通过多媒体让学生观察毕达哥拉斯家的磁砖2、提问:是否任意直角三角形三边都符合等腰直角三角形三边的这个关系?引导学生由特殊到一般。3、由多媒体打出网格,在网格中给出任意三角形,引导学生到格点图中去验证自己的猜测。由于网格的不规则,引出用割补的方法进行计算。 独立、仔细观察1分钟,然后4人一小组讨并派代表发表观点结论:a2+b2=c2猜测并回答结果小组讨论并举手回答:割补方法不一。原则:不规则经过割补变为规则。
二、实验探究,证明结论为了让学生感受数形结合这一数学思想,利用多媒体,要求学生由两块面积为a2与b2组成的图形经割补变为c2。↓提问:由以上过程,你能得到什么结论?由此我们得到了证明勾股定理的一种方法:等积法。 学生课前准备了“L”形,要求学生亲自动手,互相协助,将“L”形进行割补。学生回答:因为是割下来再补上去,所以前后面积相等。由此得到:a2+b2=c2
三、练兵之际用多媒体打出“总统证法”的图形问题:你能用此图形证明勾股定理吗? 独立思考举手回答:用“等积法”可证。
四、自己动手,拼出弦图让学生提前准备了四个全等的边长为a、b、c的直角三角形进行拼图。问题:你能用拼出的图形证明勾股定理吗? 小组合作,进行拼图。上黑板将拼图粘贴在黑板上进行演示。
总结反思点拨要位 1、通过这节课,你学到了哪些知识?2、通过这节课的学习过程,说说你的感受? 1、学到了用“等积法”证明勾股定理及数形结合的思想。2、感受到了数学的奇妙,也感受到了古人的伟大。我们一定要将此传承下去。
作业布置 让学生制作一份与勾股定理有关的数学小报。
A
B
C
A
B
C
b
C2
b
c
c
a
a
b
A
D
C
D
c
b
c
b
c
a
b
c
a
b
c
a
a
一、学情分析
学生经历了一年的初中学习,具备了一定的归纳、总结、类比、转化以及数学表达的能力,对现实生活中的数学知识充满了强烈的好奇心与探究欲,并能在老师的指导下通过小组成员间的互助合作,发表自己的见解。另外,在学本节课时,通过前置知识的学习,学生对直角三角形有了初步的认识,并能从直观把握直角三角形的一些特征,为此在授课时要抓住学生的这些特点,激发学生学习数学的兴趣,建立他们的自信心,为学生空间观念的发展、数学活动经验的积累、个性的发挥提供机会。
二、教材分析
(一)本节内容分析
本节课是勾股定理的第1课时,根据课程标准的要求,注意让学生经历探索勾股定理的过程,鼓励学生用不同的方法解决问题,在解决问题的过程中,注意渗透数形结合的思想。另外,勾股定理具有很高的文化价值,这点要充分体现,以提高学生探索的欲望。
(二)教学目标
1、经历探索勾股定理的过程,提高学生的推理能力,体会数形结合的思想。
2、理解并掌握勾股定理。
3、通过对勾股定理的历史介绍及交流,让学生体会它的文化价值,提高学习数学的兴趣和信心。
(三)教学重难点
1、教学重点:掌握勾股定理,让学生深刻感悟到直角三角形三边所具备的特殊关系。
2、教学难点:勾股定理的证明
三、教学设计
教学环节 教 师 活 动 学 生 活 动
创设情境引入新课 利用多媒体介绍在北京召开的2002年国际数学大会会标“赵爽弦图”,激发学生学习兴趣和民族自豪感 聆听并感受
师生互动探索新知 一、观察、发现、类比、猜测1、通过多媒体让学生观察毕达哥拉斯家的磁砖2、提问:是否任意直角三角形三边都符合等腰直角三角形三边的这个关系?引导学生由特殊到一般。3、由多媒体打出网格,在网格中给出任意三角形,引导学生到格点图中去验证自己的猜测。由于网格的不规则,引出用割补的方法进行计算。 独立、仔细观察1分钟,然后4人一小组讨并派代表发表观点结论:a2+b2=c2猜测并回答结果小组讨论并举手回答:割补方法不一。原则:不规则经过割补变为规则。
二、实验探究,证明结论为了让学生感受数形结合这一数学思想,利用多媒体,要求学生由两块面积为a2与b2组成的图形经割补变为c2。↓提问:由以上过程,你能得到什么结论?由此我们得到了证明勾股定理的一种方法:等积法。 学生课前准备了“L”形,要求学生亲自动手,互相协助,将“L”形进行割补。学生回答:因为是割下来再补上去,所以前后面积相等。由此得到:a2+b2=c2
三、练兵之际用多媒体打出“总统证法”的图形问题:你能用此图形证明勾股定理吗? 独立思考举手回答:用“等积法”可证。
四、自己动手,拼出弦图让学生提前准备了四个全等的边长为a、b、c的直角三角形进行拼图。问题:你能用拼出的图形证明勾股定理吗? 小组合作,进行拼图。上黑板将拼图粘贴在黑板上进行演示。
总结反思点拨要位 1、通过这节课,你学到了哪些知识?2、通过这节课的学习过程,说说你的感受? 1、学到了用“等积法”证明勾股定理及数形结合的思想。2、感受到了数学的奇妙,也感受到了古人的伟大。我们一定要将此传承下去。
作业布置 让学生制作一份与勾股定理有关的数学小报。
A
B
C
A
B
C
b
C2
b
c
c
a
a
b
A
D
C
D
c
b
c
b
c
a
b
c
a
b
c
a
a
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
