2022-2023学年浙江省宁波市浙教版八年级数学上册第5章一次函数选择题专练(含解析)
文档属性
| 名称 | 2022-2023学年浙江省宁波市浙教版八年级数学上册第5章一次函数选择题专练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 316.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-02 12:22:36 | ||
图片预览



文档简介
第5章《一次函数》选择题专练 2022-2023学年浙江省宁波市浙教版八年级数学上册
一.选择题(共29小题)
1.(2021秋 北仑区期末)已知直线y=﹣3x+4过点A(﹣1,y1)和点(﹣3,y2),则y1和y2的大小关系是( )
A.y1>y2 B.y1<y2 C.y1=y2 D.不能确定
2.(2021秋 江北区期中)一次函数y=﹣2x﹣1的图象大致是( )
A. B.
C. D.
3.(2022春 鄞州区校级月考)函数y自变量x的取值范围为( )
A.x>﹣1 B.x<﹣1 C.x≠﹣1 D.x≠0
4.(2021秋 鄞州区校级月考)以固定的速度v0(米/秒)向上抛一个小球,小球的高度h(米)与小球的运动的时间t(秒)之间的关系式是h=v0t﹣4.9t2,在这个关系式中,常量、变量分别为( )
A.4.9是常量,t、h是变量
B.v0是常量,t、h是变量
C.v0、﹣4.9是常量,t、h是变量
D.4.9是常量,v0、t、h是变量
5.(2021秋 宁波期末)一次函数y=﹣4x+2的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.(2022秋 镇海区校级期中)已知(﹣3,y1)(﹣1,y2),(,y3)是直线yx+2上的三个点,则y1,y2,y3的大小关系是( )
A.y1>y2>y3 B.y3>y2>y1 C.y1>y3>y2 D.y3>y1>y2
7.(2021秋 鄞州区校级月考)下列函数中,自变量x的取值范围选取错误的是( )
A.y=2x2中,x取全体实数
B.y中,x取x≠﹣1的实数
C.y中,x取x≥2的实数
D.y中,x取x≥﹣3的实数
8.(2021秋 海曙区期末)如图,点C的坐标为(4,5),CA垂直于y轴于点A,D是线段AO上一点,且OD=4AD,点B从原点O出发,沿x轴正方向运动,CB与直线yx交于点E,取OE的中点F,则△CFD的面积为( )
A.10 B.9 C. D.8
9.(2021秋 海曙区校级期末)在平面直角坐标系中,若点(x1,﹣1),(x2,﹣2),(x3,1)都在直线y=﹣2x+b上,则x1,x2,x3的大小关系是( )
A.x1>x2>x3 B.x3>x2>x1 C.x2>x3>x1 D.x2>x1>x3
10.(2022秋 鄞州区校级期中)2022年2月5日,电影《长津湖》在青海剧场首映,小李一家开车去观看.最初以某一速度匀速行驶,中途停车加油耽误了十几分钟,为了按时到达剧场,小李在不违反交通规则的前提下加快了速度,仍保持匀速行驶.在此行驶过程中,汽车离剧场的距离y(千米)与行驶时间t(小时)的函数关系的大致图象是( )
A. B.
C. D.
11.(2021秋 镇海区校级期中)直线y=﹣2x+b上有三个点(,y1),(﹣1.5,y2),(1.3,y3),则y1,y2,y3的大小关系是( )
A.y1>y2>y3 B.y1<y2<y3 C.y2>y1>y3 D.y2<y1<y3
12.(2022秋 慈溪市月考)已知点P(a,b)在直线y=﹣3x﹣4上,且2a﹣5b≤0,则下列不等式一定成立的是( )
A. B. C. D.
13.(2021秋 鄞州区校级月考)某商场为了增加销售额,推出“七月销售大酬宾”活动,其活动内容为:“凡七月份在该商场一次性购物超过100元以上者,超过100元的部分按9折优惠.”在大酬宾活动中,小王到该商场为单位购买单价为60元的办公用品x件(x>2),则应付货款y(元)与商品件数x的函数关系式是( )
A.y=54x(x>2) B.y=54x+10(x>2)
C.y=54x+90(x>2) D.y=54x+100(x>2)
14.(2021秋 鄞州区校级月考)函数中自变量x的取值范围是( )
A.x≥﹣2 B.x≥﹣2且x≠1 C.x>﹣2且x≠1 D.x≠1
15.(2021秋 鄞州区校级月考)若点A(2,﹣3),B(4,3),C(5,m)在同一直线上,则m的值为( )
A.6 B.﹣6 C.±6 D.3或6
16.(2021秋 海曙区期末)在A、B两地之间有汽车站C,甲车由A地驶往C站,乙车由B地驶往A地,两车同时出发,匀速行驶,甲、乙两车离C站的距离y1,y2(千米)与行驶时间x(小时)之间的函数图象如图所示,则下列结论:①A、B两地相距360千米;②甲车速度比乙车速度快15千米/时;③乙车行驶11小时后到达A地;④两车行驶4.4小时后相遇.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
17.(2021秋 镇海区校级期末)若关于x的不等式组无解,则一次函数y=(a﹣6)x﹣2的图象一定不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
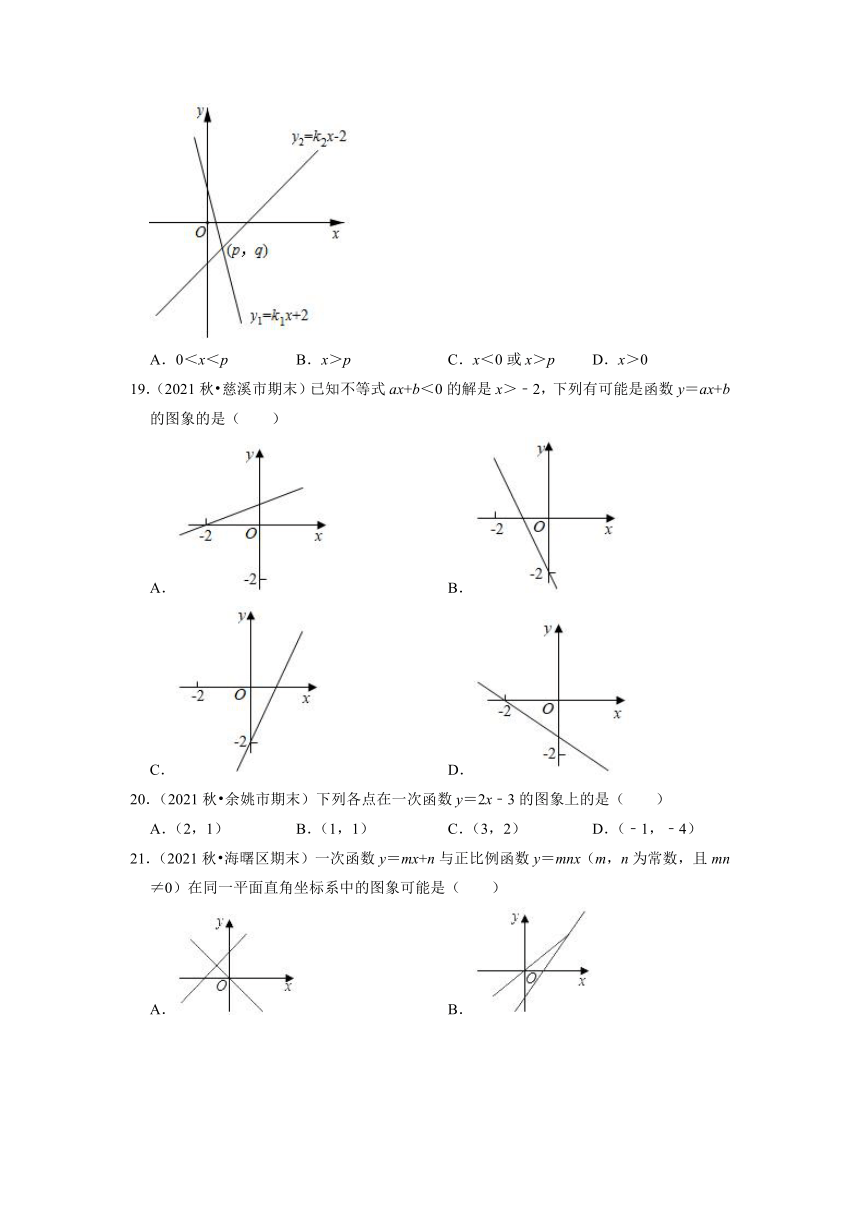
18.(2021秋 北仑区期末)在直角坐标系中,直线y1=k1x+2(k1<0)与直线y2=k2x﹣2(k2>0)的图象如图,两直线的交点坐标为(p,q),那么不等式|k1x+2|<|k2x﹣2|的解集为( )
A.0<x<p B.x>p C.x<0或x>p D.x>0
19.(2021秋 慈溪市期末)已知不等式ax+b<0的解是x>﹣2,下列有可能是函数y=ax+b的图象的是( )
A. B.
C. D.
20.(2021秋 余姚市期末)下列各点在一次函数y=2x﹣3的图象上的是( )
A.(2,1) B.(1,1) C.(3,2) D.(﹣1,﹣4)
21.(2021秋 海曙区期末)一次函数y=mx+n与正比例函数y=mnx(m,n为常数,且mn≠0)在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
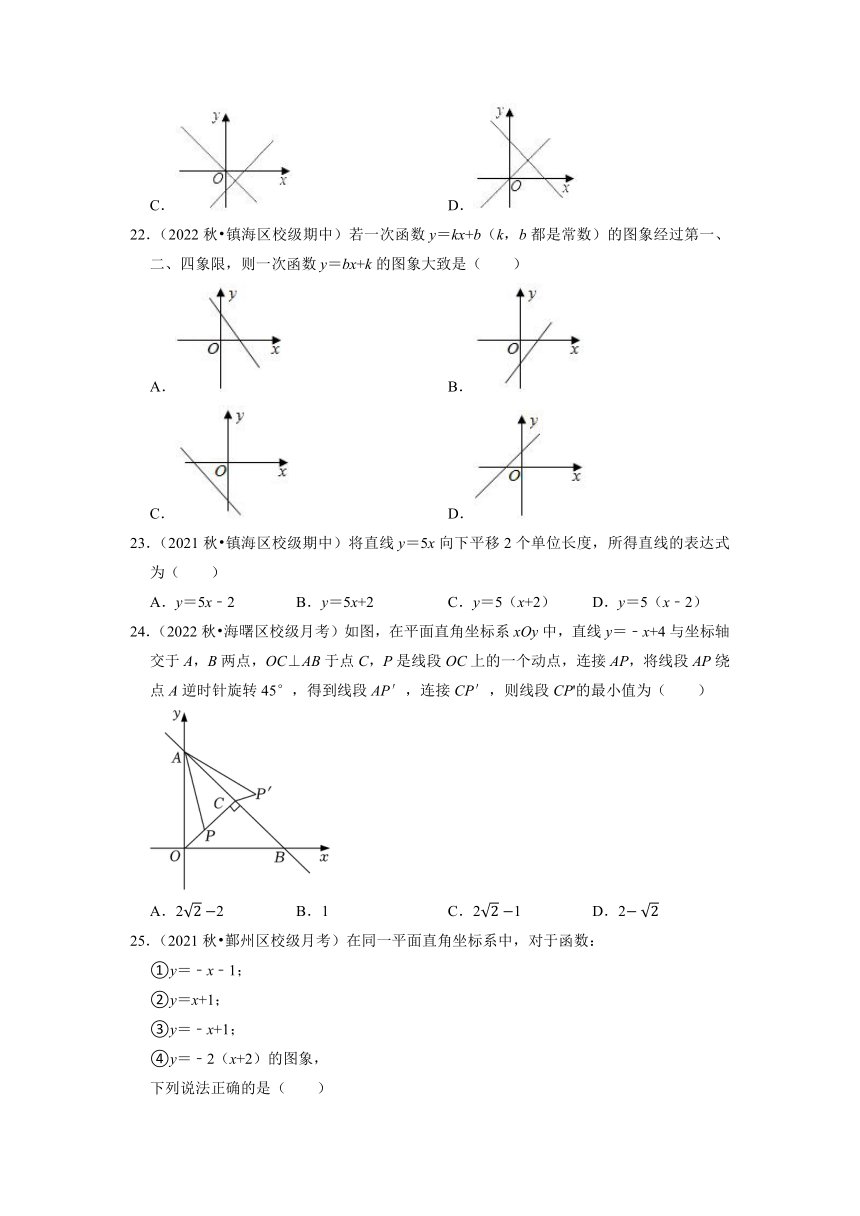
22.(2022秋 镇海区校级期中)若一次函数y=kx+b(k,b都是常数)的图象经过第一、二、四象限,则一次函数y=bx+k的图象大致是( )
A. B.
C. D.
23.(2021秋 镇海区校级期中)将直线y=5x向下平移2个单位长度,所得直线的表达式为( )
A.y=5x﹣2 B.y=5x+2 C.y=5(x+2) D.y=5(x﹣2)
24.(2022秋 海曙区校级月考)如图,在平面直角坐标系xOy中,直线y=﹣x+4与坐标轴交于A,B两点,OC⊥AB于点C,P是线段OC上的一个动点,连接AP,将线段AP绕点A逆时针旋转45°,得到线段AP′,连接CP′,则线段CP'的最小值为( )
A.22 B.1 C.21 D.2
25.(2021秋 鄞州区校级月考)在同一平面直角坐标系中,对于函数:
①y=﹣x﹣1;
②y=x+1;
③y=﹣x+1;
④y=﹣2(x+2)的图象,
下列说法正确的是( )
A.经过点(﹣1,0)的是①③
B.与y轴交点为(0,1)的是②③
C.y随x的增大而增大的是①③
D.与x轴交点为(1,0)的是②④
26.(2021秋 鄞州区校级月考)对于函数y=x﹣2,下列说法正确的是( )
A.它的图象过点(1,0)
B.y值随着x值增大而减小
C.当y>0时,x>1
D.它的图象不经过第二象限
27.(2021秋 海曙区期末)一辆轿车和一辆货车分别从甲、乙两地同时出发,匀速相向而行,相遇后继续前行,已知两车相遇时轿车比货车多行驶了90千米,设行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示从两车出发至轿车到达乙地这一过程中y与x之间的函数关系,根据图象提供的信息,以下选项中正确的个数是( )
①甲乙两地的距离为450千米;②轿车的速度为70千米/小时;③货车的速度为60千米/小时;④点C的实际意义是轿车出发5小时后到达乙地,此时两车间的距离为300千米.
A.1 B.2 C.3 D.4
28.(2021秋 海曙区校级期末)如图,一次函数y=2x+3与y轴相交于点A,与x轴相交于点B,在直线AB上取一点P(点P不与A,B重合),过点P作PQ⊥x轴,垂足为点Q,连接PO,若△PQO的面积恰好为,则满足条件的P点有( )
A.1个 B.2个 C.3个 D.4个
29.(2021秋 江北区期中)已知A,B两地相距240千米,早上9点甲车从A地出发去B地,20分钟后,乙车从B地出发去A地.两车离开各自出发地的路程y(千米)与时间x(小时)的函数关系如图所示,则下列描述不正确的是( )
A.甲车的速度是60千米/小时
B.乙车的速度是90千米/小时
C.甲车与乙车在早上10点相遇
D.乙车在12:00到达A地
第5章《一次函数》选择题专练 2022-2023学年浙江省宁波市浙教版八年级数学上册
参考答案与试题解析
一.选择题(共29小题)
1.(2021秋 北仑区期末)已知直线y=﹣3x+4过点A(﹣1,y1)和点(﹣3,y2),则y1和y2的大小关系是( )
A.y1>y2 B.y1<y2 C.y1=y2 D.不能确定
【解答】解:∵y是x的一次函数,且﹣3<0,y随x的增大而减小,且﹣1>﹣3
∴y1<y2
故选:B.
2.(2021秋 江北区期中)一次函数y=﹣2x﹣1的图象大致是( )
A. B.
C. D.
【解答】解:在y=﹣2x﹣1中,
∵﹣2<0,﹣1<0,
∴此函数的图象经过二、三、四象限,
故选:D.
3.(2022春 鄞州区校级月考)函数y自变量x的取值范围为( )
A.x>﹣1 B.x<﹣1 C.x≠﹣1 D.x≠0
【解答】解:∵x+1≠0,
∴x≠﹣1,
∴函数y自变量x的取值范围为x≠﹣1,
故选:C.
4.(2021秋 鄞州区校级月考)以固定的速度v0(米/秒)向上抛一个小球,小球的高度h(米)与小球的运动的时间t(秒)之间的关系式是h=v0t﹣4.9t2,在这个关系式中,常量、变量分别为( )
A.4.9是常量,t、h是变量
B.v0是常量,t、h是变量
C.v0、﹣4.9是常量,t、h是变量
D.4.9是常量,v0、t、h是变量
【解答】解:h=v0t﹣4.9t2中的v0(米/秒)是固定的速度,﹣4.9是定值,
故v0和﹣4.9是常量,t、h是变量,
故选:C.
5.(2021秋 宁波期末)一次函数y=﹣4x+2的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【解答】解:∵一次函数y=﹣4x+2中,k=﹣4<0,b=2>0,
∴此函数的图象经过第一、二、四象限,
∴此函数的图象不经过第三象限.
故选:C.
6.(2022秋 镇海区校级期中)已知(﹣3,y1)(﹣1,y2),(,y3)是直线yx+2上的三个点,则y1,y2,y3的大小关系是( )
A.y1>y2>y3 B.y3>y2>y1 C.y1>y3>y2 D.y3>y1>y2
【解答】解:∵k0,
∴y随x的增大而减小,
又∵(﹣3,y1)(﹣1,y2),(,y3)是直线yx+2上的三个点,﹣3<﹣1,
∴y1>y2>y3.
故选:A.
7.(2021秋 鄞州区校级月考)下列函数中,自变量x的取值范围选取错误的是( )
A.y=2x2中,x取全体实数
B.y中,x取x≠﹣1的实数
C.y中,x取x≥2的实数
D.y中,x取x≥﹣3的实数
【解答】解:A、y=2x2中,x取全体实数,本选项说法正确,不符合题意;
B、y中,x+1≠0,即x≠﹣1,本选项说法正确,不符合题意;
C、y中,x﹣2≥0,即x≥2,本选项说法正确,不符合题意;
D、y中,x+3>0,即x>﹣3,本选项说法错误,符合题意;
故选:D.
8.(2021秋 海曙区期末)如图,点C的坐标为(4,5),CA垂直于y轴于点A,D是线段AO上一点,且OD=4AD,点B从原点O出发,沿x轴正方向运动,CB与直线yx交于点E,取OE的中点F,则△CFD的面积为( )
A.10 B.9 C. D.8
【解答】解:连接OC,
∵点C的坐标为(4,5),CA垂直于y轴,
∴点A的坐标为(0,5),
∵OD=4AD,
∵AD=1,OD=4,
∴点D的坐标为(0,4),
∴设直线CD的解析式为y=kx+b,
代入C,D坐标得:,
解得:k,
∴直线CD的解析式为yx+4,
∵直线OE:yx和直线CD的解析式k值相等,
∴CD∥OE,
∴S△CFD=S△COD,
∵S△CODCA×DO,
4×4,
=8,
∴S△CFD=8,
故选:D.
9.(2021秋 海曙区校级期末)在平面直角坐标系中,若点(x1,﹣1),(x2,﹣2),(x3,1)都在直线y=﹣2x+b上,则x1,x2,x3的大小关系是( )
A.x1>x2>x3 B.x3>x2>x1 C.x2>x3>x1 D.x2>x1>x3
【解答】解:∵y=﹣2x+b,
∴y随x增大而减小,
∵1>﹣1>﹣2,
∴x2>x1>x3,
故选:D.
10.(2022秋 鄞州区校级期中)2022年2月5日,电影《长津湖》在青海剧场首映,小李一家开车去观看.最初以某一速度匀速行驶,中途停车加油耽误了十几分钟,为了按时到达剧场,小李在不违反交通规则的前提下加快了速度,仍保持匀速行驶.在此行驶过程中,汽车离剧场的距离y(千米)与行驶时间t(小时)的函数关系的大致图象是( )
A. B.
C. D.
【解答】解:随着时间的增多,汽车离剧场的距离y(千米)减少,排除A、C、D;
由于途中停车加油耽误了几分钟,此时时间在增多,汽车离剧场的距离y没有变化;
后来加快了速度,仍保持匀速行进,所以后来的函数图象的走势应比前面匀速前进的走势要陡.
故选:B.
11.(2021秋 镇海区校级期中)直线y=﹣2x+b上有三个点(,y1),(﹣1.5,y2),(1.3,y3),则y1,y2,y3的大小关系是( )
A.y1>y2>y3 B.y1<y2<y3 C.y2>y1>y3 D.y2<y1<y3
【解答】解:∵﹣2<0,
∴一次函数y=﹣2x+b中y随x的增大而减小,
∵﹣1.51.3,
∴y2>y1>y3.
故选:C.
12.(2022秋 慈溪市月考)已知点P(a,b)在直线y=﹣3x﹣4上,且2a﹣5b≤0,则下列不等式一定成立的是( )
A. B. C. D.
【解答】解:∵点P(a,b)在直线y=﹣3x﹣4上,
∴﹣3a﹣4=b,
又2a﹣5b≤0,
∴2a﹣5(﹣3a﹣4)≤0,
解得a0,
当a时,得b,
∴b,
∵2a﹣5b≤0,
∴2a≤5b,
∴.
故选:D.
13.(2021秋 鄞州区校级月考)某商场为了增加销售额,推出“七月销售大酬宾”活动,其活动内容为:“凡七月份在该商场一次性购物超过100元以上者,超过100元的部分按9折优惠.”在大酬宾活动中,小王到该商场为单位购买单价为60元的办公用品x件(x>2),则应付货款y(元)与商品件数x的函数关系式是( )
A.y=54x(x>2) B.y=54x+10(x>2)
C.y=54x+90(x>2) D.y=54x+100(x>2)
【解答】解:∵x>2,
∴销售价超过100元,超过部分为60x﹣100,
∴y=100+(60x﹣100)×0.9=54x+10(x>2,且x为整数),
故选:B.
14.(2021秋 鄞州区校级月考)函数中自变量x的取值范围是( )
A.x≥﹣2 B.x≥﹣2且x≠1 C.x>﹣2且x≠1 D.x≠1
【解答】解:由题意得:
x+2≥0且x﹣1≠0,
∴x≥﹣2且x≠1,
故选:B.
15.(2021秋 鄞州区校级月考)若点A(2,﹣3),B(4,3),C(5,m)在同一直线上,则m的值为( )
A.6 B.﹣6 C.±6 D.3或6
【解答】解:设直线解析式为y=kx+b,
把A(2,﹣3),B(4,3)代入得,解得,
所以直线解析式为y=3x﹣9,
把C(5,m)代入得m=3×5﹣9=6.
故选:A.
16.(2021秋 海曙区期末)在A、B两地之间有汽车站C,甲车由A地驶往C站,乙车由B地驶往A地,两车同时出发,匀速行驶,甲、乙两车离C站的距离y1,y2(千米)与行驶时间x(小时)之间的函数图象如图所示,则下列结论:①A、B两地相距360千米;②甲车速度比乙车速度快15千米/时;③乙车行驶11小时后到达A地;④两车行驶4.4小时后相遇.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
【解答】解:由函数图象可知,当x=0时,y1=360,y2=80,
∴A、C两地之间的距离是360千米,B、C两地之间的距离是80千米,
∴360+80=440(千米),
∴A、B两地相距440千米,
故①错误;
函数图象可知,甲车6小时行驶360千米,乙车2小时行驶80千米,
∴360÷6=60(千米/时),80÷2=40(千米/时),
∴甲、乙两车的速度分别为60千米/时和40千米/时,
∴60﹣40=20(千米/时),
∴甲车速度比乙车速度快20千米/时,
故②错误;
A、B两地相距440千米,乙车的速度是40千米/时,
∴440÷40=11(小时),
∴乙车行驶11小时后到达A地,
故③正确;
设y1=kx+360,
则6k+360=0,
解得k=﹣60,
∴y1=﹣60x+360;
设当2≤x≤11时,y2=mx+n,
则,
解得,
∴y2=40x﹣80,
两车相遇时,则y1=y2,
∴﹣60x+360=40x﹣80,
解得x=4.4,
∴两车行驶4.4小时后相遇,
故④正确,
∴③④正确,
故选:B.
17.(2021秋 镇海区校级期末)若关于x的不等式组无解,则一次函数y=(a﹣6)x﹣2的图象一定不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【解答】解:关于x的不等式组整理得,
∵关于x的不等式组无解,
∴3,
∴a≥7,
∴a﹣6>0,
∴一次函数y=(a﹣6)x﹣2的图象经过一、三、四象限,不经过第二象限,
故选:B.
18.(2021秋 北仑区期末)在直角坐标系中,直线y1=k1x+2(k1<0)与直线y2=k2x﹣2(k2>0)的图象如图,两直线的交点坐标为(p,q),那么不等式|k1x+2|<|k2x﹣2|的解集为( )
A.0<x<p B.x>p C.x<0或x>p D.x>0
【解答】解:观察图象可知直线y1=|k1x+2|(k1<0)与直线y2=|k2x﹣2|(k2>0)的交点为(p,﹣q),(0,2),
∴由图象可知不等式|k1x+2|<|k2x﹣2|的解集为0<x<p,
故选:A.
19.(2021秋 慈溪市期末)已知不等式ax+b<0的解是x>﹣2,下列有可能是函数y=ax+b的图象的是( )
A. B.
C. D.
【解答】解:∵不等式ax+b<0的解是x>﹣2,
∴直线y=ax+b与x轴交点为(﹣2,0)且y随x增大而减小,
故选:D.
20.(2021秋 余姚市期末)下列各点在一次函数y=2x﹣3的图象上的是( )
A.(2,1) B.(1,1) C.(3,2) D.(﹣1,﹣4)
【解答】解:A、2×2﹣3=1,原式成立,故本选项正确;
B、2×1﹣3=﹣1≠1,原式不成立,故本选项错误;
C、2×3﹣3=3≠2,原式不成立,故本选项错误;
D、2×(﹣1)﹣3=﹣5≠﹣4,原式不成立,故本选项错误.
故选:A.
21.(2021秋 海曙区期末)一次函数y=mx+n与正比例函数y=mnx(m,n为常数,且mn≠0)在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
【解答】解:①当mn>0,m,n同号,同正时y=mx+n过第一,二,三象限,同负时过二,三,四象限,y=mnx过原点,一、三象限;
②当mn<0时,m,n异号,则y=mx+n过一,三,四象限或一,二,四象限,y=mnx过原点,二、四象限.
解法二:本题还可用矛盾分析法来解决 A、一次函数m>0,n>0;正比例mn<0,与一次矛盾.
B、一次m>0,n<O;正比例mn>0,与一次矛盾.
C、一次m>0,n<0,正比例mn<0,成立.
D、一次m<0,n>0,正比例mn>0,矛盾.
故选:C.
22.(2022秋 镇海区校级期中)若一次函数y=kx+b(k,b都是常数)的图象经过第一、二、四象限,则一次函数y=bx+k的图象大致是( )
A. B.
C. D.
【解答】解:一次函数y=kx+b过一、二、四象限,
则函数值y随x的增大而减小,因而k<0;
图象与y轴的正半轴相交则b>0,
因而一次函数y=bx﹣k的一次项系数b>0,
y随x的增大而增大,经过一三象限,
常数项k<0,则函数与y轴负半轴相交,
因而一定经过一三四象限,
故选:B.
23.(2021秋 镇海区校级期中)将直线y=5x向下平移2个单位长度,所得直线的表达式为( )
A.y=5x﹣2 B.y=5x+2 C.y=5(x+2) D.y=5(x﹣2)
【解答】解:将直线y=5x向下平移2个单位长度,所得的函数解析式为y=5x﹣2.
故选:A.
24.(2022秋 海曙区校级月考)如图,在平面直角坐标系xOy中,直线y=﹣x+4与坐标轴交于A,B两点,OC⊥AB于点C,P是线段OC上的一个动点,连接AP,将线段AP绕点A逆时针旋转45°,得到线段AP′,连接CP′,则线段CP'的最小值为( )
A.22 B.1 C.21 D.2
【解答】解:由已知可得A(0,4)B(4,0),
∴三角形OAB是等腰直角三角形,
∵OC⊥AB,
∴C(2,2),
又∵P是线段OC上动点,将线段AP绕点A逆时针旋转45°,
∵P在线段OC上运动,所以P'的运动轨迹也是线段,
当P在O点时和P在C点时分别确定P'的起点与终点,
∴P'的运动轨迹是在与x轴垂直的一段线段MN,
∴当线段CP′与MN垂直时,线段CP′的值最小,
在△AOB中,AO=AN=4,AB=4,
∴NB=4 4,
又∵Rt△HBN是等腰直角三角形,
∴HB=4 2,
∴CP'=OB BH 2=4 (4 2) 2=2 2.
故选:A.
25.(2021秋 鄞州区校级月考)在同一平面直角坐标系中,对于函数:
①y=﹣x﹣1;
②y=x+1;
③y=﹣x+1;
④y=﹣2(x+2)的图象,
下列说法正确的是( )
A.经过点(﹣1,0)的是①③
B.与y轴交点为(0,1)的是②③
C.y随x的增大而增大的是①③
D.与x轴交点为(1,0)的是②④
【解答】解:A、分别把点(﹣1,0)代入函数解析式可知,通过点(﹣1,0)的是①②,故说法错误;
B、分别把点(0,1)代入函数解析式可知,与y轴交点为(0,1)的是②③,故说法正确;
C、由k的值可知,y随x的增大而增大的是②,故说法错误;
D、分别把点(1,0)代入函数解析式可知,与x轴交点为(1,0)的是③,故说法错误;
故选:B.
26.(2021秋 鄞州区校级月考)对于函数y=x﹣2,下列说法正确的是( )
A.它的图象过点(1,0)
B.y值随着x值增大而减小
C.当y>0时,x>1
D.它的图象不经过第二象限
【解答】解:A、它的图象过点(1,﹣1),不符合题意;
B、由于函数y=x﹣2中k=1>0,所以y值随着x值增大而增大,不符合题意;
C、当y>0时,x>2,不符合题意;
D、由于函数y=x﹣2中k=1>0,b=﹣2<0,所以该函数图象经过第一、三、四象限,即不经过第二象限,符合题意.
故选:D.
27.(2021秋 海曙区期末)一辆轿车和一辆货车分别从甲、乙两地同时出发,匀速相向而行,相遇后继续前行,已知两车相遇时轿车比货车多行驶了90千米,设行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示从两车出发至轿车到达乙地这一过程中y与x之间的函数关系,根据图象提供的信息,以下选项中正确的个数是( )
①甲乙两地的距离为450千米;②轿车的速度为70千米/小时;③货车的速度为60千米/小时;④点C的实际意义是轿车出发5小时后到达乙地,此时两车间的距离为300千米.
A.1 B.2 C.3 D.4
【解答】解:由图象可得,
甲、乙两地的距离为:150×3=450(千米),故①正确;
∵两车相遇时轿车比货车多行驶了90千米,
∴轿车每小时比货车多行驶90÷3=30(千米),
∴轿车的速度为:(450÷3+30)÷2=90(千米/小时),故②错误;
货车的速度为:(450÷3﹣30)÷2=60(千米/小时),故③正确;
点C的实际意义是轿车出发450÷90=5小时后到达乙地,此时两车间的距离为:(90+60)×(5﹣3)=300(千米),故④正确;
故选:C.
28.(2021秋 海曙区校级期末)如图,一次函数y=2x+3与y轴相交于点A,与x轴相交于点B,在直线AB上取一点P(点P不与A,B重合),过点P作PQ⊥x轴,垂足为点Q,连接PO,若△PQO的面积恰好为,则满足条件的P点有( )
A.1个 B.2个 C.3个 D.4个
【解答】解:∵点P在直线AB上,
∴设P(m,2m+3),
①当P点在第一象限时,
,
∴2m2+3m,
2m2+3m0,
Δ=18>0,
x,
m1,m2,
∵P点在第一象限,
∴P(,)
②当P点在第二象限时,
∴S△POQ,
∴,
2m2+3m0,
Δ=0,
m0,
∴P(,);
③当P点在第三象限时,
,
解得m1,m2,
∵P点在第三象限,
∴P(,),
综上所述:P(,)或P(,)或P(,).
故选:C.
29.(2021秋 江北区期中)已知A,B两地相距240千米,早上9点甲车从A地出发去B地,20分钟后,乙车从B地出发去A地.两车离开各自出发地的路程y(千米)与时间x(小时)的函数关系如图所示,则下列描述不正确的是( )
A.甲车的速度是60千米/小时
B.乙车的速度是90千米/小时
C.甲车与乙车在早上10点相遇
D.乙车在12:00到达A地
【解答】解:由题意可知,
甲车的速度是:240÷4=60(千米/小时),故选项A不合题意;
乙车的速度是:60÷()=90(千米/小时),故选项B不合题意;
设甲出发x小时后两车相遇,则60x+90(x)=240,
解得x,
所以甲车与乙车在早上10时48分相遇,故选项C符合题意;
乙车到达A地的时间为:10+(240﹣60)÷90=12(时),故选项D不合题意;
故选:C.
一.选择题(共29小题)
1.(2021秋 北仑区期末)已知直线y=﹣3x+4过点A(﹣1,y1)和点(﹣3,y2),则y1和y2的大小关系是( )
A.y1>y2 B.y1<y2 C.y1=y2 D.不能确定
2.(2021秋 江北区期中)一次函数y=﹣2x﹣1的图象大致是( )
A. B.
C. D.
3.(2022春 鄞州区校级月考)函数y自变量x的取值范围为( )
A.x>﹣1 B.x<﹣1 C.x≠﹣1 D.x≠0
4.(2021秋 鄞州区校级月考)以固定的速度v0(米/秒)向上抛一个小球,小球的高度h(米)与小球的运动的时间t(秒)之间的关系式是h=v0t﹣4.9t2,在这个关系式中,常量、变量分别为( )
A.4.9是常量,t、h是变量
B.v0是常量,t、h是变量
C.v0、﹣4.9是常量,t、h是变量
D.4.9是常量,v0、t、h是变量
5.(2021秋 宁波期末)一次函数y=﹣4x+2的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.(2022秋 镇海区校级期中)已知(﹣3,y1)(﹣1,y2),(,y3)是直线yx+2上的三个点,则y1,y2,y3的大小关系是( )
A.y1>y2>y3 B.y3>y2>y1 C.y1>y3>y2 D.y3>y1>y2
7.(2021秋 鄞州区校级月考)下列函数中,自变量x的取值范围选取错误的是( )
A.y=2x2中,x取全体实数
B.y中,x取x≠﹣1的实数
C.y中,x取x≥2的实数
D.y中,x取x≥﹣3的实数
8.(2021秋 海曙区期末)如图,点C的坐标为(4,5),CA垂直于y轴于点A,D是线段AO上一点,且OD=4AD,点B从原点O出发,沿x轴正方向运动,CB与直线yx交于点E,取OE的中点F,则△CFD的面积为( )
A.10 B.9 C. D.8
9.(2021秋 海曙区校级期末)在平面直角坐标系中,若点(x1,﹣1),(x2,﹣2),(x3,1)都在直线y=﹣2x+b上,则x1,x2,x3的大小关系是( )
A.x1>x2>x3 B.x3>x2>x1 C.x2>x3>x1 D.x2>x1>x3
10.(2022秋 鄞州区校级期中)2022年2月5日,电影《长津湖》在青海剧场首映,小李一家开车去观看.最初以某一速度匀速行驶,中途停车加油耽误了十几分钟,为了按时到达剧场,小李在不违反交通规则的前提下加快了速度,仍保持匀速行驶.在此行驶过程中,汽车离剧场的距离y(千米)与行驶时间t(小时)的函数关系的大致图象是( )
A. B.
C. D.
11.(2021秋 镇海区校级期中)直线y=﹣2x+b上有三个点(,y1),(﹣1.5,y2),(1.3,y3),则y1,y2,y3的大小关系是( )
A.y1>y2>y3 B.y1<y2<y3 C.y2>y1>y3 D.y2<y1<y3
12.(2022秋 慈溪市月考)已知点P(a,b)在直线y=﹣3x﹣4上,且2a﹣5b≤0,则下列不等式一定成立的是( )
A. B. C. D.
13.(2021秋 鄞州区校级月考)某商场为了增加销售额,推出“七月销售大酬宾”活动,其活动内容为:“凡七月份在该商场一次性购物超过100元以上者,超过100元的部分按9折优惠.”在大酬宾活动中,小王到该商场为单位购买单价为60元的办公用品x件(x>2),则应付货款y(元)与商品件数x的函数关系式是( )
A.y=54x(x>2) B.y=54x+10(x>2)
C.y=54x+90(x>2) D.y=54x+100(x>2)
14.(2021秋 鄞州区校级月考)函数中自变量x的取值范围是( )
A.x≥﹣2 B.x≥﹣2且x≠1 C.x>﹣2且x≠1 D.x≠1
15.(2021秋 鄞州区校级月考)若点A(2,﹣3),B(4,3),C(5,m)在同一直线上,则m的值为( )
A.6 B.﹣6 C.±6 D.3或6
16.(2021秋 海曙区期末)在A、B两地之间有汽车站C,甲车由A地驶往C站,乙车由B地驶往A地,两车同时出发,匀速行驶,甲、乙两车离C站的距离y1,y2(千米)与行驶时间x(小时)之间的函数图象如图所示,则下列结论:①A、B两地相距360千米;②甲车速度比乙车速度快15千米/时;③乙车行驶11小时后到达A地;④两车行驶4.4小时后相遇.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
17.(2021秋 镇海区校级期末)若关于x的不等式组无解,则一次函数y=(a﹣6)x﹣2的图象一定不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
18.(2021秋 北仑区期末)在直角坐标系中,直线y1=k1x+2(k1<0)与直线y2=k2x﹣2(k2>0)的图象如图,两直线的交点坐标为(p,q),那么不等式|k1x+2|<|k2x﹣2|的解集为( )
A.0<x<p B.x>p C.x<0或x>p D.x>0
19.(2021秋 慈溪市期末)已知不等式ax+b<0的解是x>﹣2,下列有可能是函数y=ax+b的图象的是( )
A. B.
C. D.
20.(2021秋 余姚市期末)下列各点在一次函数y=2x﹣3的图象上的是( )
A.(2,1) B.(1,1) C.(3,2) D.(﹣1,﹣4)
21.(2021秋 海曙区期末)一次函数y=mx+n与正比例函数y=mnx(m,n为常数,且mn≠0)在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
22.(2022秋 镇海区校级期中)若一次函数y=kx+b(k,b都是常数)的图象经过第一、二、四象限,则一次函数y=bx+k的图象大致是( )
A. B.
C. D.
23.(2021秋 镇海区校级期中)将直线y=5x向下平移2个单位长度,所得直线的表达式为( )
A.y=5x﹣2 B.y=5x+2 C.y=5(x+2) D.y=5(x﹣2)
24.(2022秋 海曙区校级月考)如图,在平面直角坐标系xOy中,直线y=﹣x+4与坐标轴交于A,B两点,OC⊥AB于点C,P是线段OC上的一个动点,连接AP,将线段AP绕点A逆时针旋转45°,得到线段AP′,连接CP′,则线段CP'的最小值为( )
A.22 B.1 C.21 D.2
25.(2021秋 鄞州区校级月考)在同一平面直角坐标系中,对于函数:
①y=﹣x﹣1;
②y=x+1;
③y=﹣x+1;
④y=﹣2(x+2)的图象,
下列说法正确的是( )
A.经过点(﹣1,0)的是①③
B.与y轴交点为(0,1)的是②③
C.y随x的增大而增大的是①③
D.与x轴交点为(1,0)的是②④
26.(2021秋 鄞州区校级月考)对于函数y=x﹣2,下列说法正确的是( )
A.它的图象过点(1,0)
B.y值随着x值增大而减小
C.当y>0时,x>1
D.它的图象不经过第二象限
27.(2021秋 海曙区期末)一辆轿车和一辆货车分别从甲、乙两地同时出发,匀速相向而行,相遇后继续前行,已知两车相遇时轿车比货车多行驶了90千米,设行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示从两车出发至轿车到达乙地这一过程中y与x之间的函数关系,根据图象提供的信息,以下选项中正确的个数是( )
①甲乙两地的距离为450千米;②轿车的速度为70千米/小时;③货车的速度为60千米/小时;④点C的实际意义是轿车出发5小时后到达乙地,此时两车间的距离为300千米.
A.1 B.2 C.3 D.4
28.(2021秋 海曙区校级期末)如图,一次函数y=2x+3与y轴相交于点A,与x轴相交于点B,在直线AB上取一点P(点P不与A,B重合),过点P作PQ⊥x轴,垂足为点Q,连接PO,若△PQO的面积恰好为,则满足条件的P点有( )
A.1个 B.2个 C.3个 D.4个
29.(2021秋 江北区期中)已知A,B两地相距240千米,早上9点甲车从A地出发去B地,20分钟后,乙车从B地出发去A地.两车离开各自出发地的路程y(千米)与时间x(小时)的函数关系如图所示,则下列描述不正确的是( )
A.甲车的速度是60千米/小时
B.乙车的速度是90千米/小时
C.甲车与乙车在早上10点相遇
D.乙车在12:00到达A地
第5章《一次函数》选择题专练 2022-2023学年浙江省宁波市浙教版八年级数学上册
参考答案与试题解析
一.选择题(共29小题)
1.(2021秋 北仑区期末)已知直线y=﹣3x+4过点A(﹣1,y1)和点(﹣3,y2),则y1和y2的大小关系是( )
A.y1>y2 B.y1<y2 C.y1=y2 D.不能确定
【解答】解:∵y是x的一次函数,且﹣3<0,y随x的增大而减小,且﹣1>﹣3
∴y1<y2
故选:B.
2.(2021秋 江北区期中)一次函数y=﹣2x﹣1的图象大致是( )
A. B.
C. D.
【解答】解:在y=﹣2x﹣1中,
∵﹣2<0,﹣1<0,
∴此函数的图象经过二、三、四象限,
故选:D.
3.(2022春 鄞州区校级月考)函数y自变量x的取值范围为( )
A.x>﹣1 B.x<﹣1 C.x≠﹣1 D.x≠0
【解答】解:∵x+1≠0,
∴x≠﹣1,
∴函数y自变量x的取值范围为x≠﹣1,
故选:C.
4.(2021秋 鄞州区校级月考)以固定的速度v0(米/秒)向上抛一个小球,小球的高度h(米)与小球的运动的时间t(秒)之间的关系式是h=v0t﹣4.9t2,在这个关系式中,常量、变量分别为( )
A.4.9是常量,t、h是变量
B.v0是常量,t、h是变量
C.v0、﹣4.9是常量,t、h是变量
D.4.9是常量,v0、t、h是变量
【解答】解:h=v0t﹣4.9t2中的v0(米/秒)是固定的速度,﹣4.9是定值,
故v0和﹣4.9是常量,t、h是变量,
故选:C.
5.(2021秋 宁波期末)一次函数y=﹣4x+2的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【解答】解:∵一次函数y=﹣4x+2中,k=﹣4<0,b=2>0,
∴此函数的图象经过第一、二、四象限,
∴此函数的图象不经过第三象限.
故选:C.
6.(2022秋 镇海区校级期中)已知(﹣3,y1)(﹣1,y2),(,y3)是直线yx+2上的三个点,则y1,y2,y3的大小关系是( )
A.y1>y2>y3 B.y3>y2>y1 C.y1>y3>y2 D.y3>y1>y2
【解答】解:∵k0,
∴y随x的增大而减小,
又∵(﹣3,y1)(﹣1,y2),(,y3)是直线yx+2上的三个点,﹣3<﹣1,
∴y1>y2>y3.
故选:A.
7.(2021秋 鄞州区校级月考)下列函数中,自变量x的取值范围选取错误的是( )
A.y=2x2中,x取全体实数
B.y中,x取x≠﹣1的实数
C.y中,x取x≥2的实数
D.y中,x取x≥﹣3的实数
【解答】解:A、y=2x2中,x取全体实数,本选项说法正确,不符合题意;
B、y中,x+1≠0,即x≠﹣1,本选项说法正确,不符合题意;
C、y中,x﹣2≥0,即x≥2,本选项说法正确,不符合题意;
D、y中,x+3>0,即x>﹣3,本选项说法错误,符合题意;
故选:D.
8.(2021秋 海曙区期末)如图,点C的坐标为(4,5),CA垂直于y轴于点A,D是线段AO上一点,且OD=4AD,点B从原点O出发,沿x轴正方向运动,CB与直线yx交于点E,取OE的中点F,则△CFD的面积为( )
A.10 B.9 C. D.8
【解答】解:连接OC,
∵点C的坐标为(4,5),CA垂直于y轴,
∴点A的坐标为(0,5),
∵OD=4AD,
∵AD=1,OD=4,
∴点D的坐标为(0,4),
∴设直线CD的解析式为y=kx+b,
代入C,D坐标得:,
解得:k,
∴直线CD的解析式为yx+4,
∵直线OE:yx和直线CD的解析式k值相等,
∴CD∥OE,
∴S△CFD=S△COD,
∵S△CODCA×DO,
4×4,
=8,
∴S△CFD=8,
故选:D.
9.(2021秋 海曙区校级期末)在平面直角坐标系中,若点(x1,﹣1),(x2,﹣2),(x3,1)都在直线y=﹣2x+b上,则x1,x2,x3的大小关系是( )
A.x1>x2>x3 B.x3>x2>x1 C.x2>x3>x1 D.x2>x1>x3
【解答】解:∵y=﹣2x+b,
∴y随x增大而减小,
∵1>﹣1>﹣2,
∴x2>x1>x3,
故选:D.
10.(2022秋 鄞州区校级期中)2022年2月5日,电影《长津湖》在青海剧场首映,小李一家开车去观看.最初以某一速度匀速行驶,中途停车加油耽误了十几分钟,为了按时到达剧场,小李在不违反交通规则的前提下加快了速度,仍保持匀速行驶.在此行驶过程中,汽车离剧场的距离y(千米)与行驶时间t(小时)的函数关系的大致图象是( )
A. B.
C. D.
【解答】解:随着时间的增多,汽车离剧场的距离y(千米)减少,排除A、C、D;
由于途中停车加油耽误了几分钟,此时时间在增多,汽车离剧场的距离y没有变化;
后来加快了速度,仍保持匀速行进,所以后来的函数图象的走势应比前面匀速前进的走势要陡.
故选:B.
11.(2021秋 镇海区校级期中)直线y=﹣2x+b上有三个点(,y1),(﹣1.5,y2),(1.3,y3),则y1,y2,y3的大小关系是( )
A.y1>y2>y3 B.y1<y2<y3 C.y2>y1>y3 D.y2<y1<y3
【解答】解:∵﹣2<0,
∴一次函数y=﹣2x+b中y随x的增大而减小,
∵﹣1.51.3,
∴y2>y1>y3.
故选:C.
12.(2022秋 慈溪市月考)已知点P(a,b)在直线y=﹣3x﹣4上,且2a﹣5b≤0,则下列不等式一定成立的是( )
A. B. C. D.
【解答】解:∵点P(a,b)在直线y=﹣3x﹣4上,
∴﹣3a﹣4=b,
又2a﹣5b≤0,
∴2a﹣5(﹣3a﹣4)≤0,
解得a0,
当a时,得b,
∴b,
∵2a﹣5b≤0,
∴2a≤5b,
∴.
故选:D.
13.(2021秋 鄞州区校级月考)某商场为了增加销售额,推出“七月销售大酬宾”活动,其活动内容为:“凡七月份在该商场一次性购物超过100元以上者,超过100元的部分按9折优惠.”在大酬宾活动中,小王到该商场为单位购买单价为60元的办公用品x件(x>2),则应付货款y(元)与商品件数x的函数关系式是( )
A.y=54x(x>2) B.y=54x+10(x>2)
C.y=54x+90(x>2) D.y=54x+100(x>2)
【解答】解:∵x>2,
∴销售价超过100元,超过部分为60x﹣100,
∴y=100+(60x﹣100)×0.9=54x+10(x>2,且x为整数),
故选:B.
14.(2021秋 鄞州区校级月考)函数中自变量x的取值范围是( )
A.x≥﹣2 B.x≥﹣2且x≠1 C.x>﹣2且x≠1 D.x≠1
【解答】解:由题意得:
x+2≥0且x﹣1≠0,
∴x≥﹣2且x≠1,
故选:B.
15.(2021秋 鄞州区校级月考)若点A(2,﹣3),B(4,3),C(5,m)在同一直线上,则m的值为( )
A.6 B.﹣6 C.±6 D.3或6
【解答】解:设直线解析式为y=kx+b,
把A(2,﹣3),B(4,3)代入得,解得,
所以直线解析式为y=3x﹣9,
把C(5,m)代入得m=3×5﹣9=6.
故选:A.
16.(2021秋 海曙区期末)在A、B两地之间有汽车站C,甲车由A地驶往C站,乙车由B地驶往A地,两车同时出发,匀速行驶,甲、乙两车离C站的距离y1,y2(千米)与行驶时间x(小时)之间的函数图象如图所示,则下列结论:①A、B两地相距360千米;②甲车速度比乙车速度快15千米/时;③乙车行驶11小时后到达A地;④两车行驶4.4小时后相遇.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
【解答】解:由函数图象可知,当x=0时,y1=360,y2=80,
∴A、C两地之间的距离是360千米,B、C两地之间的距离是80千米,
∴360+80=440(千米),
∴A、B两地相距440千米,
故①错误;
函数图象可知,甲车6小时行驶360千米,乙车2小时行驶80千米,
∴360÷6=60(千米/时),80÷2=40(千米/时),
∴甲、乙两车的速度分别为60千米/时和40千米/时,
∴60﹣40=20(千米/时),
∴甲车速度比乙车速度快20千米/时,
故②错误;
A、B两地相距440千米,乙车的速度是40千米/时,
∴440÷40=11(小时),
∴乙车行驶11小时后到达A地,
故③正确;
设y1=kx+360,
则6k+360=0,
解得k=﹣60,
∴y1=﹣60x+360;
设当2≤x≤11时,y2=mx+n,
则,
解得,
∴y2=40x﹣80,
两车相遇时,则y1=y2,
∴﹣60x+360=40x﹣80,
解得x=4.4,
∴两车行驶4.4小时后相遇,
故④正确,
∴③④正确,
故选:B.
17.(2021秋 镇海区校级期末)若关于x的不等式组无解,则一次函数y=(a﹣6)x﹣2的图象一定不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【解答】解:关于x的不等式组整理得,
∵关于x的不等式组无解,
∴3,
∴a≥7,
∴a﹣6>0,
∴一次函数y=(a﹣6)x﹣2的图象经过一、三、四象限,不经过第二象限,
故选:B.
18.(2021秋 北仑区期末)在直角坐标系中,直线y1=k1x+2(k1<0)与直线y2=k2x﹣2(k2>0)的图象如图,两直线的交点坐标为(p,q),那么不等式|k1x+2|<|k2x﹣2|的解集为( )
A.0<x<p B.x>p C.x<0或x>p D.x>0
【解答】解:观察图象可知直线y1=|k1x+2|(k1<0)与直线y2=|k2x﹣2|(k2>0)的交点为(p,﹣q),(0,2),
∴由图象可知不等式|k1x+2|<|k2x﹣2|的解集为0<x<p,
故选:A.
19.(2021秋 慈溪市期末)已知不等式ax+b<0的解是x>﹣2,下列有可能是函数y=ax+b的图象的是( )
A. B.
C. D.
【解答】解:∵不等式ax+b<0的解是x>﹣2,
∴直线y=ax+b与x轴交点为(﹣2,0)且y随x增大而减小,
故选:D.
20.(2021秋 余姚市期末)下列各点在一次函数y=2x﹣3的图象上的是( )
A.(2,1) B.(1,1) C.(3,2) D.(﹣1,﹣4)
【解答】解:A、2×2﹣3=1,原式成立,故本选项正确;
B、2×1﹣3=﹣1≠1,原式不成立,故本选项错误;
C、2×3﹣3=3≠2,原式不成立,故本选项错误;
D、2×(﹣1)﹣3=﹣5≠﹣4,原式不成立,故本选项错误.
故选:A.
21.(2021秋 海曙区期末)一次函数y=mx+n与正比例函数y=mnx(m,n为常数,且mn≠0)在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
【解答】解:①当mn>0,m,n同号,同正时y=mx+n过第一,二,三象限,同负时过二,三,四象限,y=mnx过原点,一、三象限;
②当mn<0时,m,n异号,则y=mx+n过一,三,四象限或一,二,四象限,y=mnx过原点,二、四象限.
解法二:本题还可用矛盾分析法来解决 A、一次函数m>0,n>0;正比例mn<0,与一次矛盾.
B、一次m>0,n<O;正比例mn>0,与一次矛盾.
C、一次m>0,n<0,正比例mn<0,成立.
D、一次m<0,n>0,正比例mn>0,矛盾.
故选:C.
22.(2022秋 镇海区校级期中)若一次函数y=kx+b(k,b都是常数)的图象经过第一、二、四象限,则一次函数y=bx+k的图象大致是( )
A. B.
C. D.
【解答】解:一次函数y=kx+b过一、二、四象限,
则函数值y随x的增大而减小,因而k<0;
图象与y轴的正半轴相交则b>0,
因而一次函数y=bx﹣k的一次项系数b>0,
y随x的增大而增大,经过一三象限,
常数项k<0,则函数与y轴负半轴相交,
因而一定经过一三四象限,
故选:B.
23.(2021秋 镇海区校级期中)将直线y=5x向下平移2个单位长度,所得直线的表达式为( )
A.y=5x﹣2 B.y=5x+2 C.y=5(x+2) D.y=5(x﹣2)
【解答】解:将直线y=5x向下平移2个单位长度,所得的函数解析式为y=5x﹣2.
故选:A.
24.(2022秋 海曙区校级月考)如图,在平面直角坐标系xOy中,直线y=﹣x+4与坐标轴交于A,B两点,OC⊥AB于点C,P是线段OC上的一个动点,连接AP,将线段AP绕点A逆时针旋转45°,得到线段AP′,连接CP′,则线段CP'的最小值为( )
A.22 B.1 C.21 D.2
【解答】解:由已知可得A(0,4)B(4,0),
∴三角形OAB是等腰直角三角形,
∵OC⊥AB,
∴C(2,2),
又∵P是线段OC上动点,将线段AP绕点A逆时针旋转45°,
∵P在线段OC上运动,所以P'的运动轨迹也是线段,
当P在O点时和P在C点时分别确定P'的起点与终点,
∴P'的运动轨迹是在与x轴垂直的一段线段MN,
∴当线段CP′与MN垂直时,线段CP′的值最小,
在△AOB中,AO=AN=4,AB=4,
∴NB=4 4,
又∵Rt△HBN是等腰直角三角形,
∴HB=4 2,
∴CP'=OB BH 2=4 (4 2) 2=2 2.
故选:A.
25.(2021秋 鄞州区校级月考)在同一平面直角坐标系中,对于函数:
①y=﹣x﹣1;
②y=x+1;
③y=﹣x+1;
④y=﹣2(x+2)的图象,
下列说法正确的是( )
A.经过点(﹣1,0)的是①③
B.与y轴交点为(0,1)的是②③
C.y随x的增大而增大的是①③
D.与x轴交点为(1,0)的是②④
【解答】解:A、分别把点(﹣1,0)代入函数解析式可知,通过点(﹣1,0)的是①②,故说法错误;
B、分别把点(0,1)代入函数解析式可知,与y轴交点为(0,1)的是②③,故说法正确;
C、由k的值可知,y随x的增大而增大的是②,故说法错误;
D、分别把点(1,0)代入函数解析式可知,与x轴交点为(1,0)的是③,故说法错误;
故选:B.
26.(2021秋 鄞州区校级月考)对于函数y=x﹣2,下列说法正确的是( )
A.它的图象过点(1,0)
B.y值随着x值增大而减小
C.当y>0时,x>1
D.它的图象不经过第二象限
【解答】解:A、它的图象过点(1,﹣1),不符合题意;
B、由于函数y=x﹣2中k=1>0,所以y值随着x值增大而增大,不符合题意;
C、当y>0时,x>2,不符合题意;
D、由于函数y=x﹣2中k=1>0,b=﹣2<0,所以该函数图象经过第一、三、四象限,即不经过第二象限,符合题意.
故选:D.
27.(2021秋 海曙区期末)一辆轿车和一辆货车分别从甲、乙两地同时出发,匀速相向而行,相遇后继续前行,已知两车相遇时轿车比货车多行驶了90千米,设行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示从两车出发至轿车到达乙地这一过程中y与x之间的函数关系,根据图象提供的信息,以下选项中正确的个数是( )
①甲乙两地的距离为450千米;②轿车的速度为70千米/小时;③货车的速度为60千米/小时;④点C的实际意义是轿车出发5小时后到达乙地,此时两车间的距离为300千米.
A.1 B.2 C.3 D.4
【解答】解:由图象可得,
甲、乙两地的距离为:150×3=450(千米),故①正确;
∵两车相遇时轿车比货车多行驶了90千米,
∴轿车每小时比货车多行驶90÷3=30(千米),
∴轿车的速度为:(450÷3+30)÷2=90(千米/小时),故②错误;
货车的速度为:(450÷3﹣30)÷2=60(千米/小时),故③正确;
点C的实际意义是轿车出发450÷90=5小时后到达乙地,此时两车间的距离为:(90+60)×(5﹣3)=300(千米),故④正确;
故选:C.
28.(2021秋 海曙区校级期末)如图,一次函数y=2x+3与y轴相交于点A,与x轴相交于点B,在直线AB上取一点P(点P不与A,B重合),过点P作PQ⊥x轴,垂足为点Q,连接PO,若△PQO的面积恰好为,则满足条件的P点有( )
A.1个 B.2个 C.3个 D.4个
【解答】解:∵点P在直线AB上,
∴设P(m,2m+3),
①当P点在第一象限时,
,
∴2m2+3m,
2m2+3m0,
Δ=18>0,
x,
m1,m2,
∵P点在第一象限,
∴P(,)
②当P点在第二象限时,
∴S△POQ,
∴,
2m2+3m0,
Δ=0,
m0,
∴P(,);
③当P点在第三象限时,
,
解得m1,m2,
∵P点在第三象限,
∴P(,),
综上所述:P(,)或P(,)或P(,).
故选:C.
29.(2021秋 江北区期中)已知A,B两地相距240千米,早上9点甲车从A地出发去B地,20分钟后,乙车从B地出发去A地.两车离开各自出发地的路程y(千米)与时间x(小时)的函数关系如图所示,则下列描述不正确的是( )
A.甲车的速度是60千米/小时
B.乙车的速度是90千米/小时
C.甲车与乙车在早上10点相遇
D.乙车在12:00到达A地
【解答】解:由题意可知,
甲车的速度是:240÷4=60(千米/小时),故选项A不合题意;
乙车的速度是:60÷()=90(千米/小时),故选项B不合题意;
设甲出发x小时后两车相遇,则60x+90(x)=240,
解得x,
所以甲车与乙车在早上10时48分相遇,故选项C符合题意;
乙车到达A地的时间为:10+(240﹣60)÷90=12(时),故选项D不合题意;
故选:C.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
