三角形综合练习(无答案)

1.已知一个三角形的两边长分别是3cm和4cm，则第三边长x的取值范围是____________________．
若x是奇数，则x的值是_______________，这样的三角形有_______个；若x是偶数，则X的值是_______________，这样的三角形又有_______个
2. 现有木棒4根,长度分别为12, 10, 8, 4, 选其中3根组成三角形,则能组成三角形的个数是( )
A.1 B.2 C.3 D.4
3. 在△ABC中，AB=6 cm，AC=8 cm那么BC长的取值范围是___________.
已知三角形的三边长为3，1+x，4，则x的取值范围是_________．
4. (1)已知△ABC有两条边长分别为2和7，另一边长是关于x的方程2x-1=4x-k+3的解，求k的取值范围．
(2)对于实数a,b,c，有下列命题：①若a＞b，则ac＜bc；②若ac2＞bc2，则a＞b；③若a＜b＜0，则a2＞ab＞b2；④若c＞a＞b＞0，则；⑤若a＞b,，则a＞0,b＜0.其中真命题的个数是（ ）
A.2 B.3 C.4 D.5
(3)如图，在△ABC中E是BC上的一点，EC=2BE，点D是AC的中点，设△ABC、△ADF、△BEF的面积分别为S△ABC，S△ADF，S△BEF，且S△ABC=12，则S△ADF-S△BEF=（ ）
5. 如图所示，在△ABC中，∠ABC=40°，AD，CD分别平分∠BAC，∠ACB，则∠ADC等于（ ）
A．110° B．100° C．190° D．120°
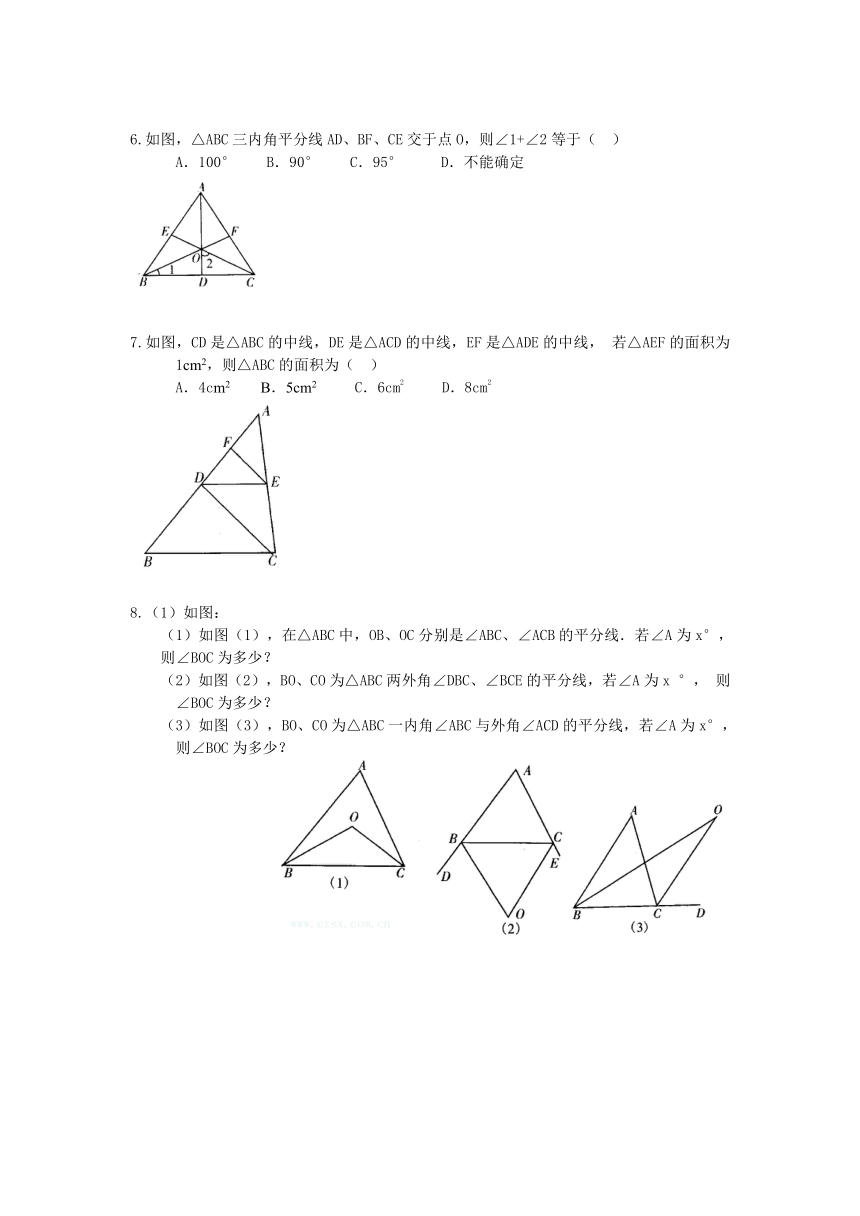
6.如图，△ABC三内角平分线AD、BF、CE交于点O，则∠1+∠2等于（ ）
A．100° B．90° C．95° D．不能确定
7.如图，CD是△ABC的中线，DE是△ACD的中线，EF是△ADE的中线，若△AEF的面积为1cm2，则△ABC的面积为（ ）
A．4cm2 B．5cm2 C．6cm2 D．8cm2
8.（1）如图：
（1）如图（1），在△ABC中，OB、OC分别是∠ABC、∠ACB的平分线．若∠A为x°， 则∠BOC为多少？
（2）如图（2），BO、CO为△ABC两外角∠DBC、∠BCE的平分线，若∠A为x°，则∠BOC为多少？
（3）如图（3），BO、CO为△ABC一内角∠ABC与外角∠ACD的平分线，若∠A为x°，则∠BOC为多少？
（2）如图，C在直线BE上，∠ABC与∠ACE的角平分线交于点A1，
（i）若∠A=60°，求∠A1的度数；
（ii）若∠A=m，求∠A1的度数；
（iii）在（2）的条件下，若再作∠A1BE、∠A1CE的平分线，交于点A2；再作∠A2BE、∠A2CE的平分线，交于点A3；…；依次类推，则∠A2，∠A3，…，∠An分别为多少度？
9.不等边△ABC的两条高长度分别为4和12，若第三条高的长也是整数，试求它的长．
10.如图，已知，，是中点，过作直线交的延长线于，交的延长线于．
求证：．
11．下列说法正确的是（ ）
A．全等三角形是指形状相同的两个三角形；
B．全等三角形是指面积相等的两个三角形
C．全等三角形的周长和面积分别相等；
D．所有等边三角形都是全等三角形
12.下列各命题中，真命题是（　　）
Ａ．如果两个三角形面积不相等，那么这两个三角形不可能全等
Ｂ．如果两个三角形不全等，那么这两个三角形面积一定不相等
Ｃ．如果，，那么与的 面积的和等于与面积的和
Ｄ.如果，，那么
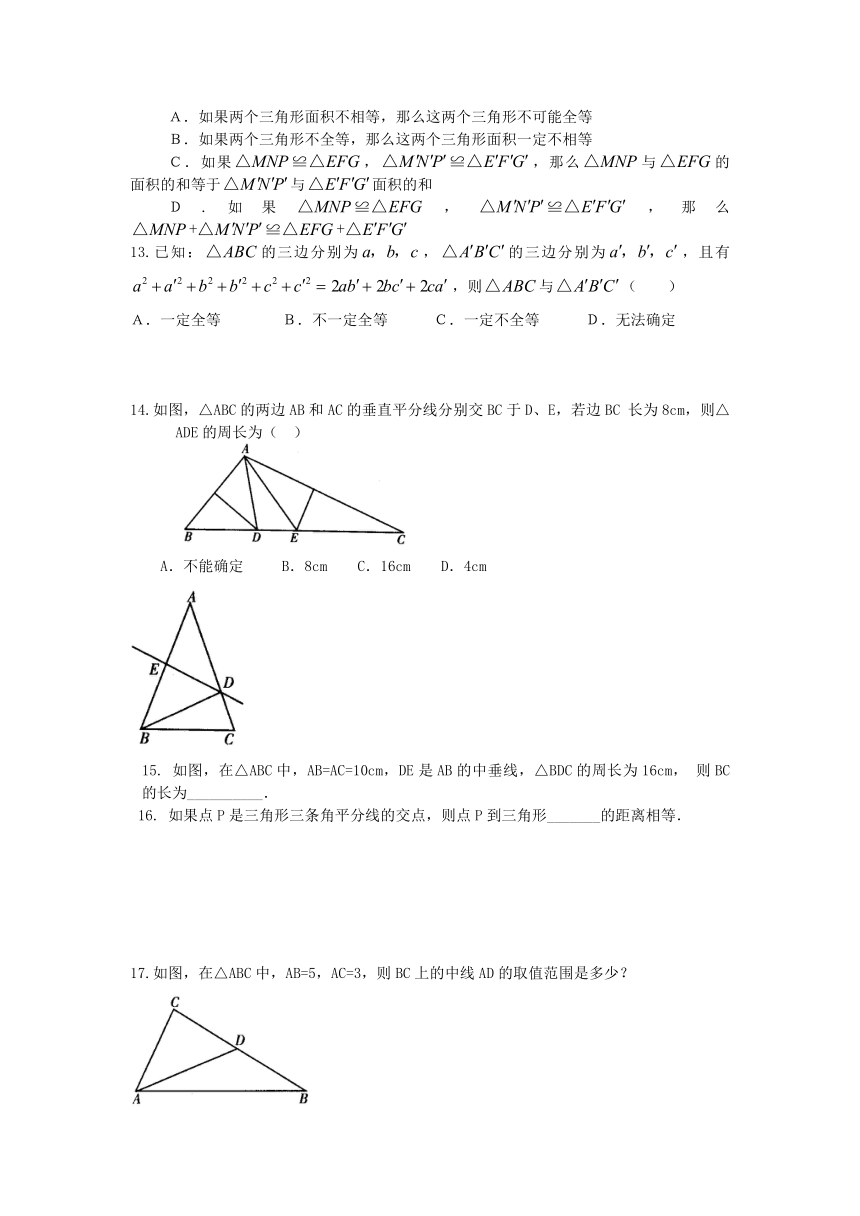
13.已知：的三边分别为，的三边分别为，且有，则与（　　）
Ａ．一定全等 Ｂ．不一定全等 Ｃ．一定不全等 Ｄ．无法确定
14.如图，△ABC的两边AB和AC的垂直平分线分别交BC于D、E，若边BC长为8cm，则△ADE的周长为（ ）
不能确定 B．8cm C．16cm D．4cm
15. 如图，在△ABC中，AB=AC=10cm，DE是AB的中垂线，△BDC的周长为16cm，则BC的长为__________．
16. 如果点P是三角形三条角平分线的交点，则点P到三角形_______的距离相等．
17.如图，在△ABC中，AB=5，AC=3，则BC上的中线AD的取值范围是多少？
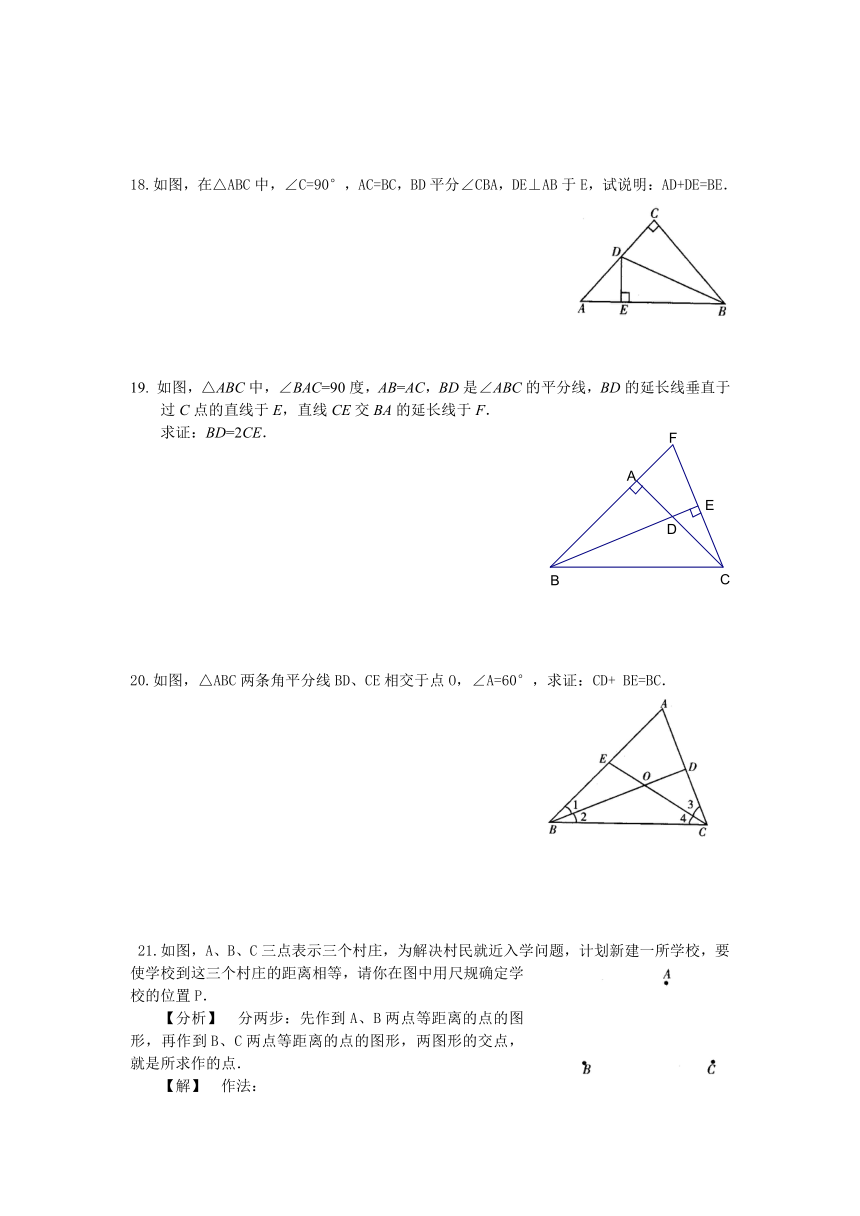
18.如图，在△ABC中，∠C=90°，AC=BC，BD平分∠CBA，DE⊥AB于E，试说明：AD+DE=BE．
19. 如图，△ABC中，∠BAC=90度，AB=AC，BD是∠ABC的平分线，BD的延长线垂直于过C点的直线于E，直线CE交BA的延长线于F．
求证：BD=2CE．
20.如图，△ABC两条角平分线BD、CE相交于点O，∠A=60°，求证：CD+BE=BC．
21.如图，A、B、C三点表示三个村庄，为解决村民就近入学问题，计划新建一所学校，要使学校到这三个村庄的距离相等，请你在图中用尺规确定学校的位置P．
【分析】 分两步：先作到A、B两点等距离的点的图形，再作到B、C两点等距离的点的图形，两图形的交点，就是所求作的点．
【解】 作法：
（1）连结AB，作线段AB的垂直平分线DE．
（2）连结BC，作线段BC的垂直平分线FG，交DE于点P．
则点P即为所求作的学校的位置（如图）．
22.如图，在△ABC中，已知BD和CE分别是两边上的中线，且BD⊥CE，BD=4，CE=6，那么△ABC的面积等于多少？
23.在△ABC中，,∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E(1)当直线MN绕点C旋转到图①的位置时，求证：DE=AD+BE
(2)当直线MN绕点C旋转到图②的位置时，求证：DE=AD-BE
(3)当直线MN绕点C旋转到图③的位置时，试问：DE、AD、BE有怎样的等量关系 请写出这个等量关系，并加以证明
24.如图，在四边形ABCD中，AC平分∠BAD，过C作CE⊥AB于E，并且,求∠ABC+∠ADC的度数。
25.七年级一班的张小明是体育委员，李聪是学习委员.这天，搞班级活动，全班同学在操场参加“小组争先”竞赛，张小明与李聪分别代表自己所在小组参加“浇花”项目竞赛.平时跑步比赛在班中数一数二的张小斌硬是在这个项目中输给了李聪，同学们百思不得其解，纷纷认真地研究起了这个问题.
这个项目的比赛是这样规定的：参赛队员同时从起点出发，先到河中打上半桶水，再跑到花坛将水浇在花丛中，最后跑回起点，先回到起点者胜.同学们都说张小斌选择的路线不对.张小明觉得很冤枉.他说：我往河边跑时跑的是最近的垂直路线，我比李聪先打的水，怎么可能不对？
聪明的同学，你知道李聪的取胜的路线吗？请你试着画一画.
26.（1）下列说法正确的是（ ）
A.等腰三角形的高、中线、角平分线互相重合
B.顶角相等的两个等腰三角形全等
C.等腰三角形一边不可是另一边的两倍
D.等腰三角形的两个底角相等
（2）在△ABC中，AB=AC, ∠A︰∠B=4︰7,求三角形的各个内角度数
（3）等腰三角形腰上的高线与底边的夹角等于（ ）
A.顶角 B.顶角的两倍 C.顶角的一半 D.底角的一半
（4）若△ABC的三边关系满足等式a2+b2+c2=ab+bc+ac，则△ABC为（ ）
A.等腰三角形 B.直角三角形 C.等边三角形 D.不能确定
（5）等边三角形的边长为a，求它的高和面积．
27.如图，BO，CO分别平分∠ABC和∠ACB，DE∥BC，AC=10cm，AB=13cm，求△ADE的周长．
28.已知：如图，点C为线段AB上一点，△ACM、△CBN是等边三角形，连结AN和BM分别与MC、NC交于点D、E,连结DE请说明下列结论成立的理由.
（1）AN=BM ；（2）△CDE是等边三角形.
29.如图，∠AOB=30 o，P是∠AOB内一点，且OP=4cm，C、D分别是P关于OA、OB的对称点，连结CD、PM、PN, 求（1）CD的长 （2）△PMN的周长
30. 如图，在△ABC中，BE, CF分别是 AC，AB边上的高，D是BC的中点，M是EF的中点，试说明DM⊥EF的理由.
31.如图，在Rt△ABC中，∠BAC=90°，AD⊥BC，D为垂足，∠ABC的平分线分别交AD，AC于点E，F，试说明：AE=AF.
32.（1）在△ABC中，三条边长分别为2n2+2n，2n+1，2n2+2n+1（n＞0）。那么△ABC是直角三角形吗？请说明理由。
（2）问：边长满足关系（a-b）（a2+b2-c2）=0的△ABC是什么三角形？
小明说△ABC是等腰三角形；小刚说△ABC是直角三角形；小亮说△ABC是等腰直角三角形；小慧说△ABC或是等腰三角形或是直角三角形或是等腰直角三角形。
亲爱的同学，你认为谁的说法正确，若都不正确，那么正确的应该怎样说呢？
33. 如图，将长方形纸片ABCD沿对角线AC折叠，使点B落在E处，若AB=4，BC=8，则（1）试判断折叠后重叠部分三角形的形状；（2）求重叠部分的面积.
34. 如图，以△ABC的每一边为边长，作三个等边三角形，所得的图形可分成五个三角形，其中，试判断△ABC是否为直角三角形，并说明理由.
35. 如图，在△ABC中，∠ABC的平分线与∠ACB的平分线交于点P，则点P必定也在∠BAC的平分线上，请说明理由.
小贴士：等边三角形具有三边相等，三角均为600的特点，往往可以利用图形变换看到全等三角形，亲爱的同学，你一定要仔细的找一找哦.
小贴士：轴对称变换一定要关注对称点连线和对称轴的关系，巧妙的把线段进行转移是本题的关键.
小贴士：等腰三角形中“三线合一”定理是说明两线垂直的重要方法，你能构造出图中的等腰三角形吗？
小贴士：想一想要证明两条线段有哪些方法？本题应如何入手？
小贴士：折叠后有很多边的长度、角的大小都是不变的，你能发现它们吗？
小贴士：题中三角形的面积应如何用△ABC的各边长来表示？