5.2函数（1）

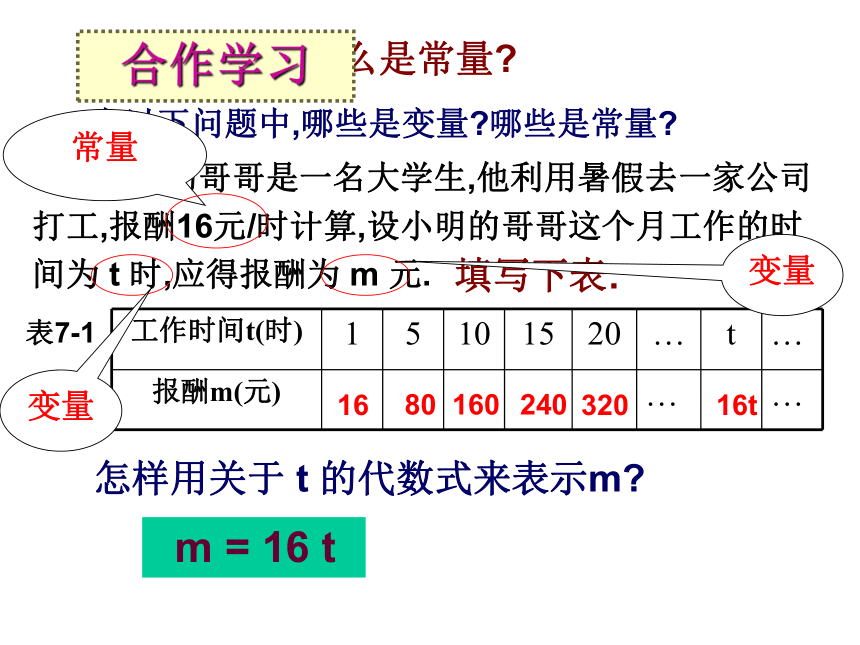
课件18张PPT。5.2认识函数 (1)什么是变量?什么是常量? 1.小明的哥哥是一名大学生,他利用暑假去一家公司打工,报酬16元/时计算,设小明的哥哥这个月工作的时间为 t 时,应得报酬为 m 元.怎样用关于 t 的代数式来表示m? 填写下表:
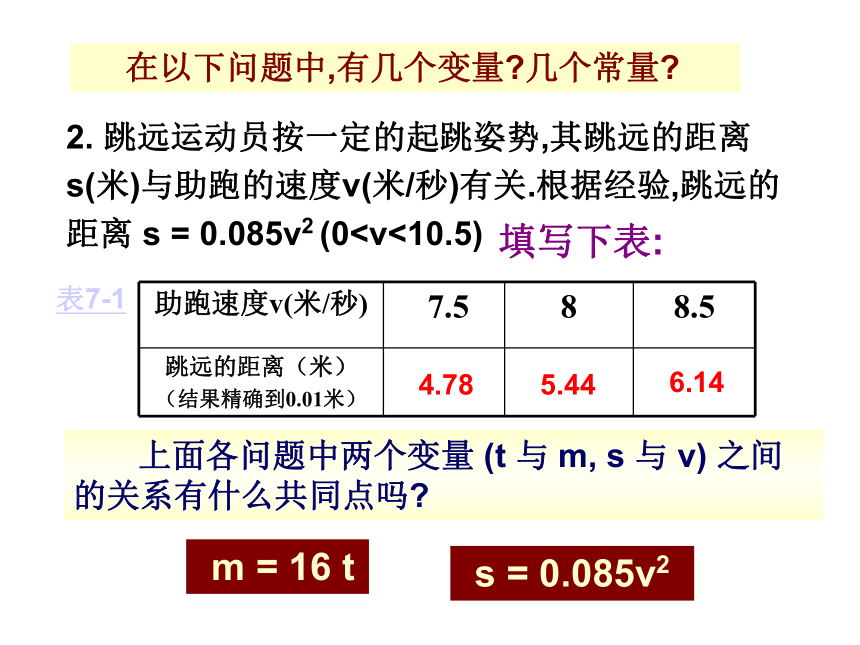
表7-1 在以下问题中,哪些是变量?哪些是常量?16t8032024016016 m = 16 t合作学习常量变量变量 在以下问题中,有几个变量?几个常量?2. 跳远运动员按一定的起跳姿势,其跳远的距离s(米)与助跑的速度v(米/秒)有关.根据经验,跳远的距离 s = 0.085v2 (0 表7-1 上面各问题中两个变量 (t 与 m, s 与 v) 之间的关系有什么共同点吗? m = 16 ts = 0.085v24.786.145.44 一般地,在某个变化过程中,设有两个变量 x, y,如果对于 x 的每一个确定的值, y 都有唯一确定的值, 那么就说 y 是 x 的函数, x 叫做自变量.上面两个问题: m = 16 t 中,___是___的函数,___是自变量; s = 0.085v2中, ___是___的函数,___是自变量.vttmvsm = 16 t, s = 0.085v2这两个函数用等式来表示,这种表示函数关系的等式,叫做函数解析式,简称函数式.用函数解析式表示函数的方法也叫解析法.书写注意：1）函数的关系式是等式;2）通常等式的左边的一个字母表示函数，
右边是含有自变量的代数式.

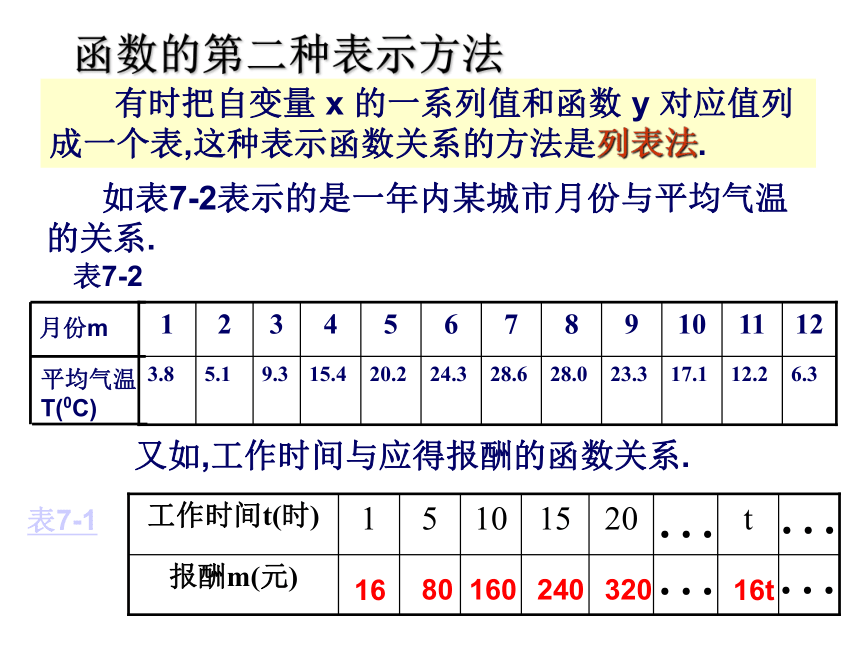
函数的概念 有时把自变量 x 的一系列值和函数 y 对应值列 成一个表,这种表示函数关系的方法是列表法. 如表7-2表示的是一年内某城市月份与平均气温的关系.又如,工作时间与应得报酬的函数关系.函数的第二种表示方法如图表示某日的气温变化情况
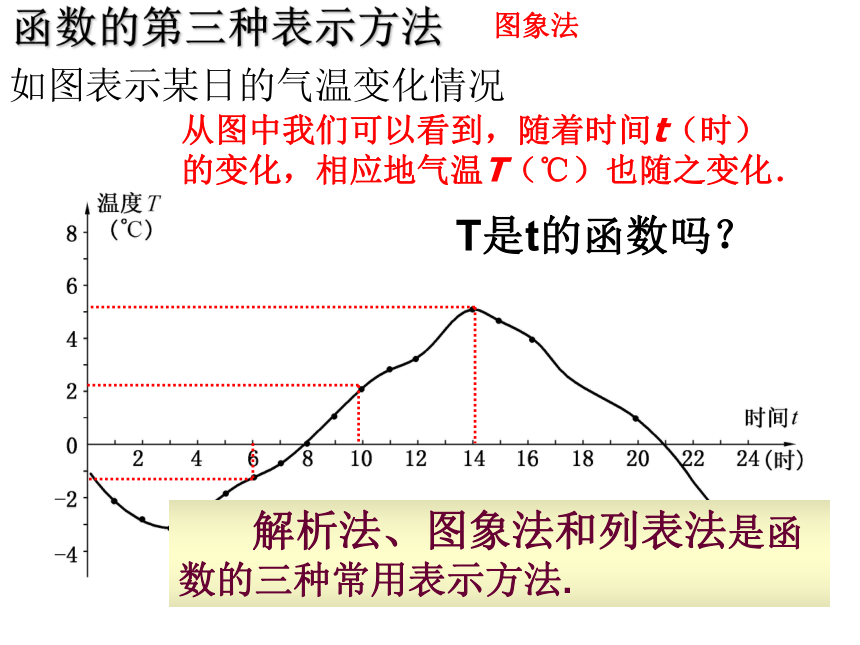
从图中我们可以看到，随着时间t（时）
的变化，相应地气温T（℃）也随之变化． T是t的函数吗？图象法函数的第三种表示方法 解析法、图象法和列表法是函数的三种常用表示方法.对于函数m=16t,当t=5时，能求得m的值吗？怎么求？在这里，我们把m=80叫做当自变量t=5 时的函数值.把它代入函数解析式，得
m=16t=16×5=80
请你思考当m=5时，函数T的值为__________.20.2求函数的值图象法 当t=10时，函数值T=_____图象法列表法解析法解析法、图象法、列表法是函数的三种常用表示方法y=2x ， S=0.085v2知识整理：查表代入画一画代一代、画一画、查一查是求函数值的三种常用表示方法
课堂练习1、下列关系中，y不是x函数的是（ ）D错误,请再想想。ABCD小试牛刀判断是不是函数，我们可以看它的数学式子中的变量之间是否满足函数的定义.2.下列四个图形中，y是x的函数图象是（ ）C做一做尝试应用：1、某市民用水费的价格是2.9元/立方米，小红准备收取她所居住大楼各用户这个月的水费。设用水量为n立方米，应付水费为m元.在这个问题中，m关于n的函数解析式是 .当n=15时，函数值是 ，这一函数值的实际意义是 . m=2.9n43.5当水量为15立方米时需交水费43.5元2.根据跳远的距离函数关系式：s=0.085v2
(0（1）分别求当v=6，v =10时的函数值，并说明它们的
实际意义；
（2）当v=16时，函数值有意义吗？为什么？1.在某个变化过程中,设有两个变量 x, y,如果对于
x 的每一个确定的值, , 那么
就说 , x 叫做 .
y 都有唯一确定的值y 是 x 的函数自变量2.函数的表示法有： ， ， .解析法
列表法
图象法
3.求函数值的方法： ， ， ， 共同回顾查一查代一代画一画学数学可是为了用数学哦！练2：下图是某水库的库容曲线图，其中x表示水库的平均水深（米），v表示水库的库容（万立方米）.依图象回答下面的问题：（1）这个函数反映了哪两个变量之间的关系？
（2）当平均水深取5米到25米之间的一个确定的值时，相应的库容v确定吗？
（3）库容v可以看成平均水深x的函数吗？
（4）求当x =20时的函数值，并说明它的实际意义.（1）下列各曲线中哪些表示 y 是 x 的函数3.下面三个的表格反映y与x的关系，其中y是x的函数的有_____个2（1）若有四封信件质量分别为5克、20克、40克和50克，则该分别付邮资多少元？（3）若有信件已付邮资1.60元，能确定该信件质量吗？(2) y是m的函数吗?答：是，因为对于m的每一个值，y都有唯一确定的值与它对应.解：分别付邮资0.80元、0.80元、1.60元、2.40元不能，只能确定该信件质量的取值范围.
(1) m是y的函数吗?答：不是，因为对于y的某一个值，m有不唯一
的值与它对应.