5.2认识函数（2）

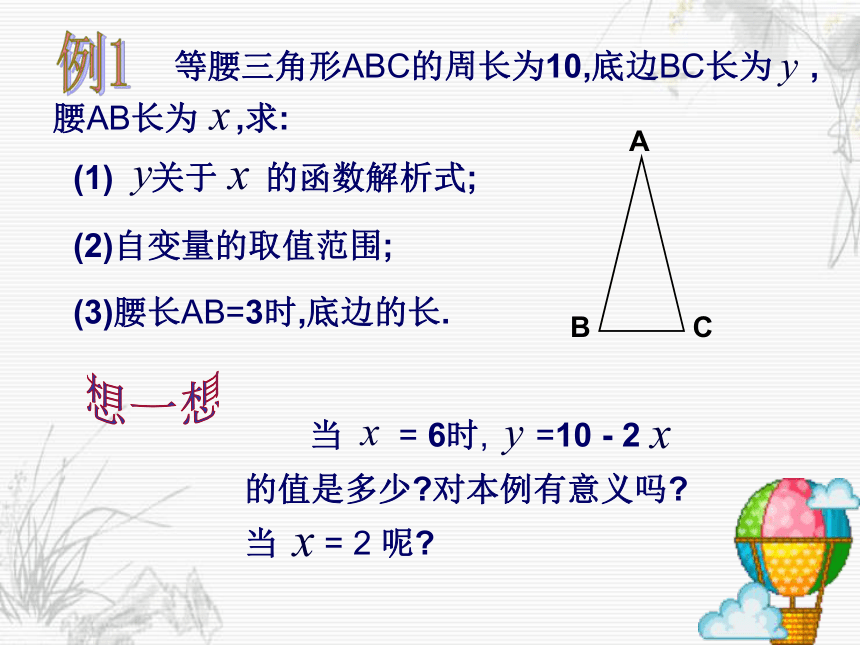
课件16张PPT。5.2函数（2）想一想一个三角形的周长为y（cm），三边长分别为7（cm），3（cm）和 x（cm）.(1) 求y关于x的函数解析式.(3) 求自变量x的取值范围.(2) 取一个你喜欢的数作为x的值，求此时y的值；y=10+x这些函数值都有实际意义吗？4∴当腰长 AB = 3 时，底边BC长为4 当 = 6时, =10 - 2 的值是多少?对本例有意义吗?当 = 2 呢?想一想ABC 求实际问题中的函数解析式，关键是寻找问题中两个变量之间的等量关系，再将它转化成用自变量来表示函数的形式.经验小结 实际问题中的函数，自变量的取值要符合实际.. 求下列函数中自变量x的取值范围：
(1) y＝3x－1； (2)y＝2x2＋7；
(3) ； (4)
一般来说，函数解析式中自变量的取值要使 代数式有意义.练一练X为任何实数X为任何实数经验小结 ①代数式有意义. 求函数自变量的取值范围时，需要考虑：②符合实际
例2:游泳池应定期换水,某游泳池在一次换水前存水936m3,换水时打开排水孔,以每时312m3 的速度将水放出.设放水时间为t时, 游泳池内的存水量为Q立方米.
(1)求Q关于t的函数解析式和自变量t的 取值范围.
(2)放水2时20分后,游泳池内还剩水多少立方米?
(3)放完游泳池内全部水需要多少时间?解:(1)Q关于t的函数解析式是Q=936 – 312 t∵Q ≥0, t ≥0解得: 0≤t≤ 3即自变量t的取值范围是0≤t ≤3把t = 代入上式,得Q=936-312× =208(立方米)放完全部水,即Q=0,即936-312t =0,解得t=3(时),所以放完全部水需要3时. ① 求函数解析式 经验小结函数的几类基本问题：自变量函数值③② 求自变量的取值范围. 如图,用长为50米的篱笆靠一片旧墙围一个猪圈，这一片旧墙最大可用的长为18米. 设猪圈靠墙一边为 x米,另一边为y米,试求：
（1）y关于x的函数解析式；
（2）自变量x的取值范围；
（3）当x=20米时，求y的值.练一练xxy（1）y=50-2x（2）x的取值范围是：（3）当x=20米时，y=10米4.如图:正方形EFGH内接于边长为1的正方形ABCD,设AE=x,试求正方形EFGH的面积y与x的函数式,写出自变量x的取值范围,并求出AE= 时,正方形EFGH的面积.1-xy =1- 4× x(1-x)=2x2 - 2x + 1(0＜x＜1)当x= 时,y =2×( )2 -2× +1=练一练探究活动 如图,每个图形都是由若干个棋子围成的正方形图案的每条边(包括两个顶点)上都有 个棋子,设每个图案的棋子总数为 S. 图中棋子的排列有什么规律? S与 n 之间能用函数解析式表示吗?自变量的取值范围是什么?如果排成的是五边形有什么规律? 能用函数解析式表示吗?今天你有什么收获?蓦然回首 家庭作业：
1. 必做题:书本p149 A组，
作业本7.2（2）；
2. 选做题:书本p149 B组；
3. 实践题:书本p149 探究活动. 谢谢大家
再见