5.5.2 两个一次函数(图象)的应用 课件(共23张PPT)
文档属性
| 名称 | 5.5.2 两个一次函数(图象)的应用 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-05 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
5.5.2两个一次函数(图象)的应用
浙教版 八年级上册
教学目标
【教学目标】
1.会综合运用一次函数的解析式和图象解决简单的实际问题。
2.了解直角坐标系中两条直线(不平行于坐标轴)的交点坐标与两条直线的函数解析式所组成的二元一次方程组的解之间的关系。
3.会用一次函数的图象求二元一次方程组的解(包括近似解)。
【重点】本节教学的重点是运用一次函数的解析式和图象等解决简单的实际问题。
【难点】构造数学模型(包括函数解析式和图象)与实际情景问题之间的对应关系,是本节教学的难点。
0
x
1
-1
-2
-3
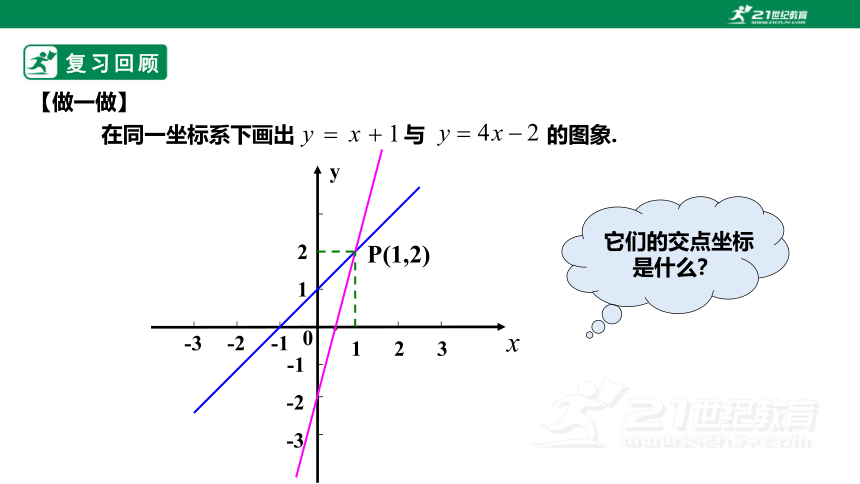
在同一坐标系下画出 与 的图象.
y
2
1
2
3
-1
-2
-3
P(1,2)
它们的交点坐标是什么?
【做一做】
复习回顾
新知探究
问题 1号探测气球从海拔5m处出发,以1m/min的速度上升.与此同时,2号探测气球从海拔15m处出发,以0.5m/min的速度上升.两个气球都上升了1小时.
(1)用式子分别表示两个气球所在位置的海拔(单位:米)关于上升时间(单位:分钟)的函数关系.
气球上升时间满足 .
分析:
1号气球的函数解析式为 ;
2号气球的函数解析式为 .
0≤x ≤60
y=x+5
y=0.5x+15
新知探究
(2)在某个时刻两个气球能否位于同一高度 如果能,这时气球上升了多长时间?位于什么高度?
分析:在某个时刻两个气球位于同一高度,就是说对于x的某个值(0≤x≤60),函数y=x+5和y=0.5x+15有相同的值y.则只需求出x和y的值.
解二元一次方程组:
y=x+5,
y=0.5x+15,
即:
x-y=-5,
0.5x-y=-15,
解得:
x=20,
y=25,
这就是说,当上升20min时,两个气球都位于海拔25m的高度.
新知探究
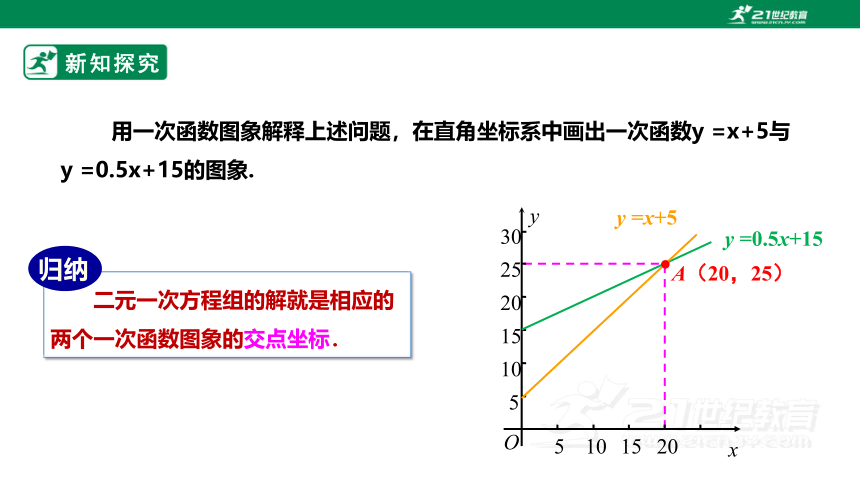
二元一次方程组的解就是相应的两个一次函数图象的交点坐标.
用一次函数图象解释上述问题,在直角坐标系中画出一次函数y =x+5与y =0.5x+15的图象.
A(20,25)
y =x+5
y =0.5x+15
30
25
20
15
10
5
10
20
15
5
O
x
y
归纳
新知探究
从“数”的角度看:解二元一次方程组,相当于求自变量为何值时相应的两个函数值相等,以及这个函数值是多少;
从“形”的角度看:解二元一次方程组,相当于确定两条直线的交点坐标.因此,我们可以用画一次函数图象的方法得到方程组的解.
一般地,因为每个含有未知数x和y的二元一次方程,都可以改写为(y=kx+b)的形式,所以每个这样的方程都对应一个一次函数,于是也对应一条直线.这条直线上每个点的坐标(x ,y)都是这个二元一次方程的解.
新知探究
例2 小聪和小慧去某风景区游览,约好在“飞瀑”见面,上午7:00,小聪乘电动汽车从“古刹”出发,沿景区公路去“飞瀑”,车速为30km/h,小慧也于上午7:00从“塔林”出发,骑电动自行车沿景区公路去“飞瀑”,车速为20km/h.
(1)当小聪追上小慧时,他们是否
已经过了“草甸”?
(2)当小聪到达“飞瀑”时,小慧
离“飞瀑”还有多少千米?
新知探究
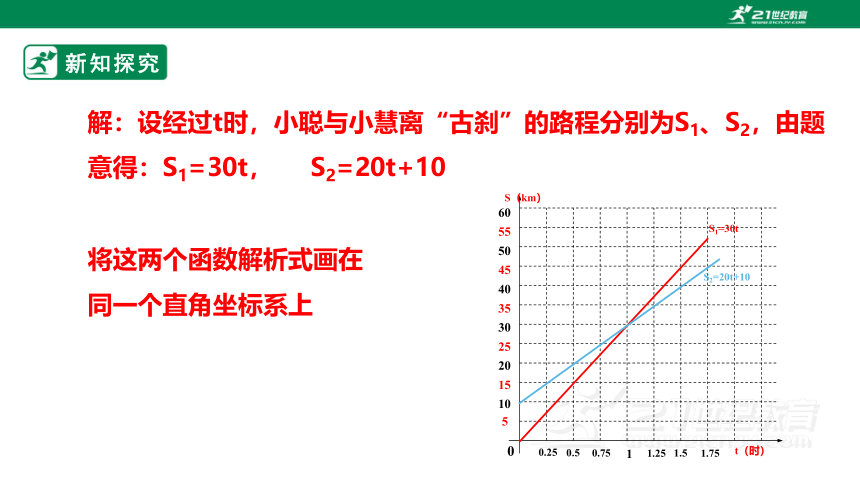
解:设经过t时,小聪与小慧离“古刹”的路程分别为S1、S2,由题意得:S1=30t, S2=20t+10
5
t(时)
S(km)
10
20
30
40
50
60
15
25
35
45
55
0.25
0
0.5
0.75
1
1.25
1.5
1.75
S1=30t
S2=20t+10
将这两个函数解析式画在同一个直角坐标系上
新知探究
5
t(时)
S(km)
10
20
30
40
50
60
15
25
35
45
55
0.25
0
0.5
0.75
1
1.25
1.5
1.75
S1=30t
S2=20t+10
(1)两条直线s=30t,s=20t+10的交点坐标为__________,所以当小聪追上小慧时,s=30 km,即离古刹30km,小于35 km,也就是说,他们还没到草甸.
(1)当小聪追上小慧时,他们是否已经过了“草甸”?
(1,30)
(1,30)
新知探究
(2)当小聪到达“飞瀑”时,小慧离“飞瀑”还有多少千米?
5
t(时)
S(km)
10
20
30
40
50
60
15
25
35
45
55
0.25
0
0.5
0.75
1
1.25
1.5
1.75
S1=30t
S2=20t+10
(2)当小聪到达“飞瀑”时,
即S1=_____km,此时S2=_____km。
所以小慧离“飞瀑”还有
______________________
45
40
45-40=5(km)
新知探究
解决方案问题步骤:
1.把实际问题转化为数学函数问题,列出函数关系式(建立数学模型).
2.通过解不等式或画函数图象的方式确定自变量的范围.
3.利用一次函数的增减性知识从而选择出最佳方案.
课堂练习
1.一次函数y=kx+b的图象如图所示,则方程kx+b=0的解为( )
A.x=2 B.y=2
C.x=-1 D.y=-1
C
课堂练习
A
2.如图所示,一次函数y=k1x+b1的图象l1与y=k2x+b2的图象l2相交于点P,则方程组 的解是( )
y=k1x+b1
y=k2x+b2
x=-2
y=3
A.
D.
C.
B.
x=3
y=-2
x=2
y=3
x=-2
y=-3
课堂练习
3.已知函数y=kx+b,当x>5时,y<0;当x<5时,y>0,则y=kx+b的图象必经过点( )
A.(0,5) B.(5,0) C.(-5,0) D.(0,-5)
B
4.若直线y=3x-1与y=x-k的交点在第四象限,则k的取值范围为_____________.
课堂练习
5.如图所示,已知函数y=3x+b和y=ax-3的图象交于点P(-2,-5),根据图象可得不等式3x+b>ax-3的解是 .
x>-2
课堂练习
6.因为方程组 的解是
所以一次函数y=-x+4与y=2x+1的图象交点坐标为 .
1
3
(1,3)
课堂练习
7.如图是甲、乙两家商店销售同一种产品的销售价 y(元)与销售量 x(件)之间的函数图象.下列说法, 其中正确的说法有 .(填序号)
①售2件时甲、乙两家售价一样;
②买1件时买乙家的合算;
③买3件时买甲家的合算;
④买1件时,售价约为3元.
①②③
课堂练习
8.已知一次函数y= x+a和y=- x+b的图象都经过点A(-4,0),且与y轴分别交于B、C两点,求△ABC的面积.
解:∵y= x+a与y=- x+b的
图象都过点A(-4,0),
∴ ×(-4)+a=0,
- ×(-4)+b=0.
∴a=6,b=-2.
∴两个一次函数分别是y= x+6和y=- x-2.
课堂练习
y= x+6与y轴交于点B,则y= ×0+6=6,
∴B(0,6);
y=- x-2与y轴交于点C,则y=-2,
∴C(0,-2).
如图所示,
S△ABC= BC·AO
= ×4×(6+2)=16.
课堂小结
(1)一次函数与二元一次方程组可以相互转化,从图象到关系式都是完美的统一.
(2)将二元一次方程组转化为两个一次函数,如果两个一次函数的图象有一个交点,那么这个交点的坐标就是这个二元一次方程组的解.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
5.5.2两个一次函数(图象)的应用
浙教版 八年级上册
教学目标
【教学目标】
1.会综合运用一次函数的解析式和图象解决简单的实际问题。
2.了解直角坐标系中两条直线(不平行于坐标轴)的交点坐标与两条直线的函数解析式所组成的二元一次方程组的解之间的关系。
3.会用一次函数的图象求二元一次方程组的解(包括近似解)。
【重点】本节教学的重点是运用一次函数的解析式和图象等解决简单的实际问题。
【难点】构造数学模型(包括函数解析式和图象)与实际情景问题之间的对应关系,是本节教学的难点。
0
x
1
-1
-2
-3
在同一坐标系下画出 与 的图象.
y
2
1
2
3
-1
-2
-3
P(1,2)
它们的交点坐标是什么?
【做一做】
复习回顾
新知探究
问题 1号探测气球从海拔5m处出发,以1m/min的速度上升.与此同时,2号探测气球从海拔15m处出发,以0.5m/min的速度上升.两个气球都上升了1小时.
(1)用式子分别表示两个气球所在位置的海拔(单位:米)关于上升时间(单位:分钟)的函数关系.
气球上升时间满足 .
分析:
1号气球的函数解析式为 ;
2号气球的函数解析式为 .
0≤x ≤60
y=x+5
y=0.5x+15
新知探究
(2)在某个时刻两个气球能否位于同一高度 如果能,这时气球上升了多长时间?位于什么高度?
分析:在某个时刻两个气球位于同一高度,就是说对于x的某个值(0≤x≤60),函数y=x+5和y=0.5x+15有相同的值y.则只需求出x和y的值.
解二元一次方程组:
y=x+5,
y=0.5x+15,
即:
x-y=-5,
0.5x-y=-15,
解得:
x=20,
y=25,
这就是说,当上升20min时,两个气球都位于海拔25m的高度.
新知探究
二元一次方程组的解就是相应的两个一次函数图象的交点坐标.
用一次函数图象解释上述问题,在直角坐标系中画出一次函数y =x+5与y =0.5x+15的图象.
A(20,25)
y =x+5
y =0.5x+15
30
25
20
15
10
5
10
20
15
5
O
x
y
归纳
新知探究
从“数”的角度看:解二元一次方程组,相当于求自变量为何值时相应的两个函数值相等,以及这个函数值是多少;
从“形”的角度看:解二元一次方程组,相当于确定两条直线的交点坐标.因此,我们可以用画一次函数图象的方法得到方程组的解.
一般地,因为每个含有未知数x和y的二元一次方程,都可以改写为(y=kx+b)的形式,所以每个这样的方程都对应一个一次函数,于是也对应一条直线.这条直线上每个点的坐标(x ,y)都是这个二元一次方程的解.
新知探究
例2 小聪和小慧去某风景区游览,约好在“飞瀑”见面,上午7:00,小聪乘电动汽车从“古刹”出发,沿景区公路去“飞瀑”,车速为30km/h,小慧也于上午7:00从“塔林”出发,骑电动自行车沿景区公路去“飞瀑”,车速为20km/h.
(1)当小聪追上小慧时,他们是否
已经过了“草甸”?
(2)当小聪到达“飞瀑”时,小慧
离“飞瀑”还有多少千米?
新知探究
解:设经过t时,小聪与小慧离“古刹”的路程分别为S1、S2,由题意得:S1=30t, S2=20t+10
5
t(时)
S(km)
10
20
30
40
50
60
15
25
35
45
55
0.25
0
0.5
0.75
1
1.25
1.5
1.75
S1=30t
S2=20t+10
将这两个函数解析式画在同一个直角坐标系上
新知探究
5
t(时)
S(km)
10
20
30
40
50
60
15
25
35
45
55
0.25
0
0.5
0.75
1
1.25
1.5
1.75
S1=30t
S2=20t+10
(1)两条直线s=30t,s=20t+10的交点坐标为__________,所以当小聪追上小慧时,s=30 km,即离古刹30km,小于35 km,也就是说,他们还没到草甸.
(1)当小聪追上小慧时,他们是否已经过了“草甸”?
(1,30)
(1,30)
新知探究
(2)当小聪到达“飞瀑”时,小慧离“飞瀑”还有多少千米?
5
t(时)
S(km)
10
20
30
40
50
60
15
25
35
45
55
0.25
0
0.5
0.75
1
1.25
1.5
1.75
S1=30t
S2=20t+10
(2)当小聪到达“飞瀑”时,
即S1=_____km,此时S2=_____km。
所以小慧离“飞瀑”还有
______________________
45
40
45-40=5(km)
新知探究
解决方案问题步骤:
1.把实际问题转化为数学函数问题,列出函数关系式(建立数学模型).
2.通过解不等式或画函数图象的方式确定自变量的范围.
3.利用一次函数的增减性知识从而选择出最佳方案.
课堂练习
1.一次函数y=kx+b的图象如图所示,则方程kx+b=0的解为( )
A.x=2 B.y=2
C.x=-1 D.y=-1
C
课堂练习
A
2.如图所示,一次函数y=k1x+b1的图象l1与y=k2x+b2的图象l2相交于点P,则方程组 的解是( )
y=k1x+b1
y=k2x+b2
x=-2
y=3
A.
D.
C.
B.
x=3
y=-2
x=2
y=3
x=-2
y=-3
课堂练习
3.已知函数y=kx+b,当x>5时,y<0;当x<5时,y>0,则y=kx+b的图象必经过点( )
A.(0,5) B.(5,0) C.(-5,0) D.(0,-5)
B
4.若直线y=3x-1与y=x-k的交点在第四象限,则k的取值范围为_____________.
课堂练习
5.如图所示,已知函数y=3x+b和y=ax-3的图象交于点P(-2,-5),根据图象可得不等式3x+b>ax-3的解是 .
x>-2
课堂练习
6.因为方程组 的解是
所以一次函数y=-x+4与y=2x+1的图象交点坐标为 .
1
3
(1,3)
课堂练习
7.如图是甲、乙两家商店销售同一种产品的销售价 y(元)与销售量 x(件)之间的函数图象.下列说法, 其中正确的说法有 .(填序号)
①售2件时甲、乙两家售价一样;
②买1件时买乙家的合算;
③买3件时买甲家的合算;
④买1件时,售价约为3元.
①②③
课堂练习
8.已知一次函数y= x+a和y=- x+b的图象都经过点A(-4,0),且与y轴分别交于B、C两点,求△ABC的面积.
解:∵y= x+a与y=- x+b的
图象都过点A(-4,0),
∴ ×(-4)+a=0,
- ×(-4)+b=0.
∴a=6,b=-2.
∴两个一次函数分别是y= x+6和y=- x-2.
课堂练习
y= x+6与y轴交于点B,则y= ×0+6=6,
∴B(0,6);
y=- x-2与y轴交于点C,则y=-2,
∴C(0,-2).
如图所示,
S△ABC= BC·AO
= ×4×(6+2)=16.
课堂小结
(1)一次函数与二元一次方程组可以相互转化,从图象到关系式都是完美的统一.
(2)将二元一次方程组转化为两个一次函数,如果两个一次函数的图象有一个交点,那么这个交点的坐标就是这个二元一次方程组的解.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
