6.7 角的和差 课件(共20张PPT)
文档属性
| 名称 | 6.7 角的和差 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 932.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-06 16:23:18 | ||
图片预览






文档简介
(共20张PPT)
6.7角的和差
浙教版 七年级上册
教学目标
教学目标:
1.了解角的和差的概念。
2.会表示两个角的和、差,会在图形中辨认角的和、差,会用量角器作两个角的和、差。
3.理解角平分线的概念,会用量角器画一个角的平分线,会进行有关的角的和、差、倍分的简单运算。
重点:角的和与差、角平分线及其意义。
难点:角的和差、角平分线等诸多概念,较多角的数量关系。
回顾复习
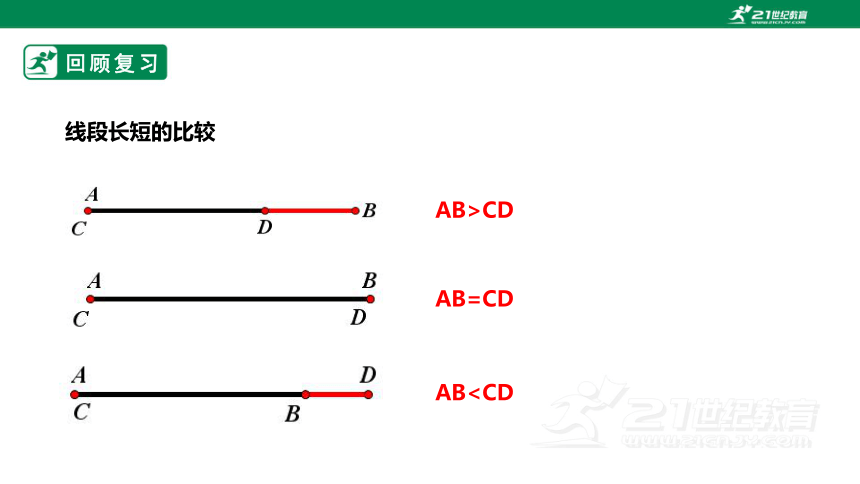
线段长短的比较
AB>CD
ABAB=CD
回顾复习
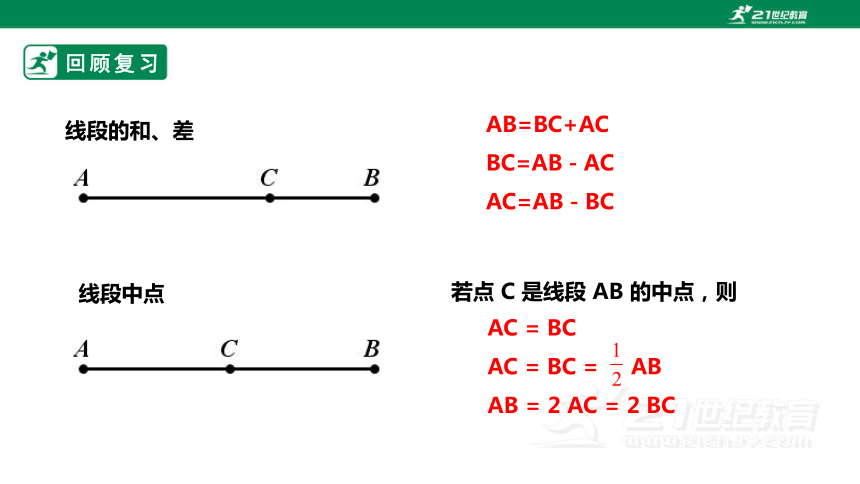
线段的和、差
线段中点
AB=BC+AC
BC=AB-AC
AC=AB-BC
若点 C 是线段 AB 的中点,则
AC = BC
AC = BC = AB
AB = 2 AC = 2 BC
新知探究
如图,已知∠α=30°,∠β=120°,∠γ=150°
请议一议,这三个角的度数之间有怎样的关系.
1.∠α+∠β=30°+120°=150°=∠γ
2.∠γ-∠β=150°-120°=30°=∠α
3.∠γ-∠α=150°-30°=120°=∠β
新知探究
一般地,如果一个角的度数是另两个角的度数的和,那么这个角就叫做另两个角的和;
如果一个角的度数是另两个角的度数的差,那么这个角就叫做另两个角的差。
注意:两个角的和或差仍是一个角.
新知探究
同一端点的三条射线如图,请完成下面的填空:
∠AOB+∠BOC=∠________=________度;
∠ AOC-∠BOC= ∠ ________=________度;
∠BOC= ∠ AOC-∠ ________=________度.
AOC
110
AOB
30
AOB
80
两个角可以相加(或相减),它们的和(或差)也是一个角.它的度数等于这两个角的度数的和(或差).
新知探究
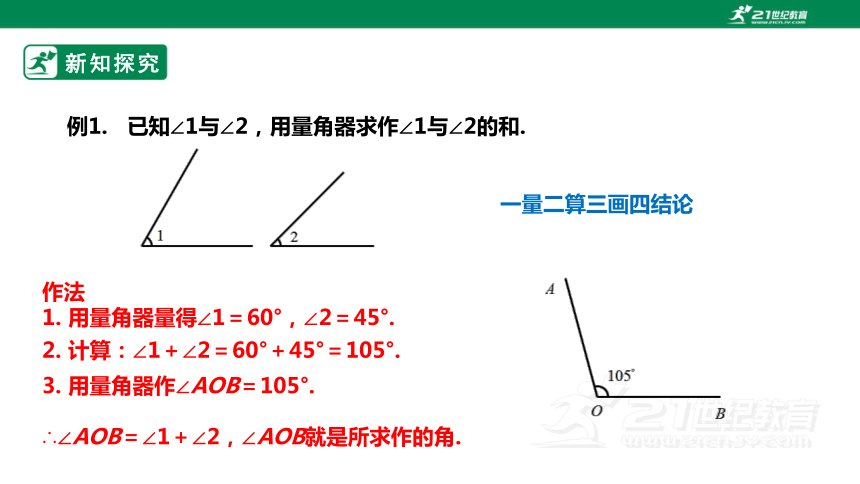
作法
1. 用量角器量得∠1=60°,∠2=45°.
一量二算三画四结论
2. 计算:∠1+∠2=60°+45°=105°.
3. 用量角器作∠AOB=105°.
∴∠AOB=∠1+∠2,∠AOB就是所求作的角.
例1. 已知∠1与∠2,用量角器求作∠1与∠2的和.
新知探究
在一张透明纸上任意画一个角∠AOB,把这张纸折叠,使角的两边OA与OB重合,然后把纸展开,画出折痕OC.问∠AOC与∠BOC之间有怎样的大小关系?
∵折叠时∠AOC与∠BOC重合,
∴ ∠AOC=∠BOC.
新知探究
一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线.
应用格式:
∵ OC 是∠AOB 的角平分线,
∴ ∠AOC =∠BOC = ∠AOB,
∠AOB =2∠BOC =2∠AOC.
O
B
A
C
注意:
角平分线是在角的内部从角的顶点引出的一条射线,不是直线或线段;
新知探究
角的n等分线:类似角的平分线,从角的顶点引出的射线,将角分成相等的n个角,叫做角的n等分线,
将一个角三等分
射线OC、OD为∠AOB的三等分线
将一个角四等分
射线OC、OD 、OE 为∠AOB的四等分线
新知探究
解:∵∠ABD=∠ABC+∠CBD
=90°+30°=120°,
BP平分∠ABD,
例2、 如图, ∠ABC=90°,∠CBD=30°,BP平分∠ABD,求∠ABP的度数.
∴ ∠ABP= ∠ABD= ×120°=60°.
课堂练习
1. 如图,OC是∠AOB的平分线,OD是∠BOC的平分线,那么下列各式中正确的是 ( )
A
O
A
B
C
D
课堂练习
2.如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=110°,则∠BOD的度数是( )
A.25° B.35° C.45° D.55°
D
课堂练习
3. 如图,∠AOB=∠COD=90°,∠AOD=146°,则∠BOC=____.
4. 已知∠AOB=38°,∠BOC=25°,那么∠AOC的度数是 .
34°
13°或63°
O
A
B
C
D
课堂练习
5. 如图,∠AOB=170°,∠AOC =∠BOD=90°,求∠COD的度数
解:因为∠AOB=170°,
∠AOC=90°,
所以∠BOC=170°-90°=80°.
所以∠DOC=∠BOD-∠BOC=90°-80°=10°.
O
A
B
C
D
课堂练习
6.如图,已知∠AOC=60°,∠BOD=90°,∠AOB是∠DOC的3倍,求∠AOB的度数.
O
A
D
C
B
解:设∠COD=x.
∵∠AOC=60°,∠BOD=90°,
∴∠AOD=60°-x,
∴∠AOB=90°+60°-x=150°-x.
∵∠AOB是∠DOC的3倍,
∴150°-x=3x,解得x=37.5°,
∴∠AOB=3×37.5°=112.5°.
课堂小结
1、角的和差及表示方法.
2、用量角器画一个角等于已知角.
3、角平分线:从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.
4、与角平分线有关的角的计算.
O
B
A
C
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
6.7角的和差
浙教版 七年级上册
教学目标
教学目标:
1.了解角的和差的概念。
2.会表示两个角的和、差,会在图形中辨认角的和、差,会用量角器作两个角的和、差。
3.理解角平分线的概念,会用量角器画一个角的平分线,会进行有关的角的和、差、倍分的简单运算。
重点:角的和与差、角平分线及其意义。
难点:角的和差、角平分线等诸多概念,较多角的数量关系。
回顾复习
线段长短的比较
AB>CD
AB
回顾复习
线段的和、差
线段中点
AB=BC+AC
BC=AB-AC
AC=AB-BC
若点 C 是线段 AB 的中点,则
AC = BC
AC = BC = AB
AB = 2 AC = 2 BC
新知探究
如图,已知∠α=30°,∠β=120°,∠γ=150°
请议一议,这三个角的度数之间有怎样的关系.
1.∠α+∠β=30°+120°=150°=∠γ
2.∠γ-∠β=150°-120°=30°=∠α
3.∠γ-∠α=150°-30°=120°=∠β
新知探究
一般地,如果一个角的度数是另两个角的度数的和,那么这个角就叫做另两个角的和;
如果一个角的度数是另两个角的度数的差,那么这个角就叫做另两个角的差。
注意:两个角的和或差仍是一个角.
新知探究
同一端点的三条射线如图,请完成下面的填空:
∠AOB+∠BOC=∠________=________度;
∠ AOC-∠BOC= ∠ ________=________度;
∠BOC= ∠ AOC-∠ ________=________度.
AOC
110
AOB
30
AOB
80
两个角可以相加(或相减),它们的和(或差)也是一个角.它的度数等于这两个角的度数的和(或差).
新知探究
作法
1. 用量角器量得∠1=60°,∠2=45°.
一量二算三画四结论
2. 计算:∠1+∠2=60°+45°=105°.
3. 用量角器作∠AOB=105°.
∴∠AOB=∠1+∠2,∠AOB就是所求作的角.
例1. 已知∠1与∠2,用量角器求作∠1与∠2的和.
新知探究
在一张透明纸上任意画一个角∠AOB,把这张纸折叠,使角的两边OA与OB重合,然后把纸展开,画出折痕OC.问∠AOC与∠BOC之间有怎样的大小关系?
∵折叠时∠AOC与∠BOC重合,
∴ ∠AOC=∠BOC.
新知探究
一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线.
应用格式:
∵ OC 是∠AOB 的角平分线,
∴ ∠AOC =∠BOC = ∠AOB,
∠AOB =2∠BOC =2∠AOC.
O
B
A
C
注意:
角平分线是在角的内部从角的顶点引出的一条射线,不是直线或线段;
新知探究
角的n等分线:类似角的平分线,从角的顶点引出的射线,将角分成相等的n个角,叫做角的n等分线,
将一个角三等分
射线OC、OD为∠AOB的三等分线
将一个角四等分
射线OC、OD 、OE 为∠AOB的四等分线
新知探究
解:∵∠ABD=∠ABC+∠CBD
=90°+30°=120°,
BP平分∠ABD,
例2、 如图, ∠ABC=90°,∠CBD=30°,BP平分∠ABD,求∠ABP的度数.
∴ ∠ABP= ∠ABD= ×120°=60°.
课堂练习
1. 如图,OC是∠AOB的平分线,OD是∠BOC的平分线,那么下列各式中正确的是 ( )
A
O
A
B
C
D
课堂练习
2.如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=110°,则∠BOD的度数是( )
A.25° B.35° C.45° D.55°
D
课堂练习
3. 如图,∠AOB=∠COD=90°,∠AOD=146°,则∠BOC=____.
4. 已知∠AOB=38°,∠BOC=25°,那么∠AOC的度数是 .
34°
13°或63°
O
A
B
C
D
课堂练习
5. 如图,∠AOB=170°,∠AOC =∠BOD=90°,求∠COD的度数
解:因为∠AOB=170°,
∠AOC=90°,
所以∠BOC=170°-90°=80°.
所以∠DOC=∠BOD-∠BOC=90°-80°=10°.
O
A
B
C
D
课堂练习
6.如图,已知∠AOC=60°,∠BOD=90°,∠AOB是∠DOC的3倍,求∠AOB的度数.
O
A
D
C
B
解:设∠COD=x.
∵∠AOC=60°,∠BOD=90°,
∴∠AOD=60°-x,
∴∠AOB=90°+60°-x=150°-x.
∵∠AOB是∠DOC的3倍,
∴150°-x=3x,解得x=37.5°,
∴∠AOB=3×37.5°=112.5°.
课堂小结
1、角的和差及表示方法.
2、用量角器画一个角等于已知角.
3、角平分线:从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.
4、与角平分线有关的角的计算.
O
B
A
C
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
