第4章 相似三角形 复习课件(22张ppt)
文档属性
| 名称 | 第4章 相似三角形 复习课件(22张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-06 19:23:05 | ||
图片预览







文档简介
(共22张PPT)
第4章 相似三角形
浙教版九年级上册
教学目标
1.巧用相似比求解与三角形有关的计算题.
2.利用相似的性质解题.
3.利用相似比解题.
温故知新
一、相似三角形的判定方法:
①通过定义:三边对应相等,三角相等
②平行于三角形一边的直线
③三边对应成比例(SSS)
④两边成比例且夹角相等(SAS)
⑤两角对应相等(AA)
温故知新
二、相似三角形的性质:
①对应角相等
②对应边成比例
③对应高的比等于相似比
④对应中线的比等于相似比
⑤对应角平分线的比等于相似比
周长之比等于相似比
面积之比等于相似比
典例讲解
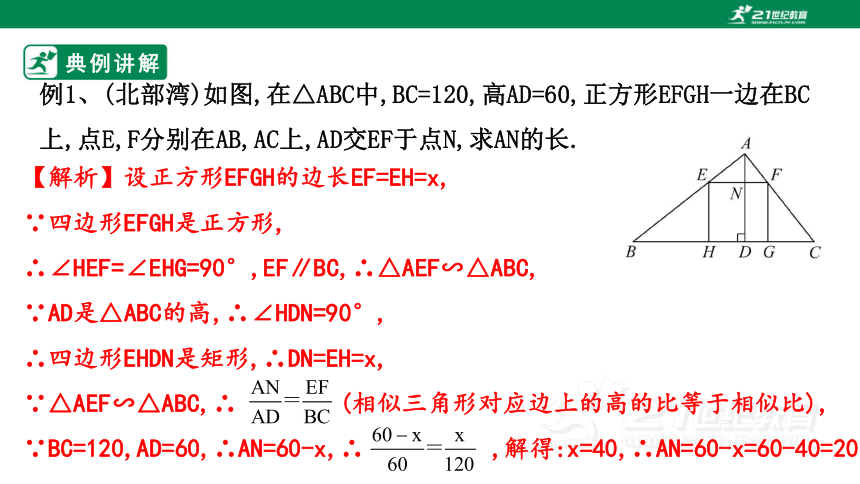
例1、(北部湾)如图,在△ABC中,BC=120,高AD=60,正方形EFGH一边在BC上,点E,F分别在AB,AC上,AD交EF于点N,求AN的长.
【解析】设正方形EFGH的边长EF=EH=x,
∵四边形EFGH是正方形,
∴∠HEF=∠EHG=90°,EF∥BC,∴△AEF∽△ABC,
∵AD是△ABC的高,∴∠HDN=90°,
∴四边形EHDN是矩形,∴DN=EH=x,
∵△AEF∽△ABC,∴ (相似三角形对应边上的高的比等于相似比),
∵BC=120,AD=60,∴AN=60-x,∴ ,解得:x=40,∴AN=60-x=60-40=20.
强化练习
1.在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”应落在下列哪个位置处,能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”、“兵”所在位置的格点构成的三角形相似( )
A.①处 B.②处
C.③处 D.④处
B
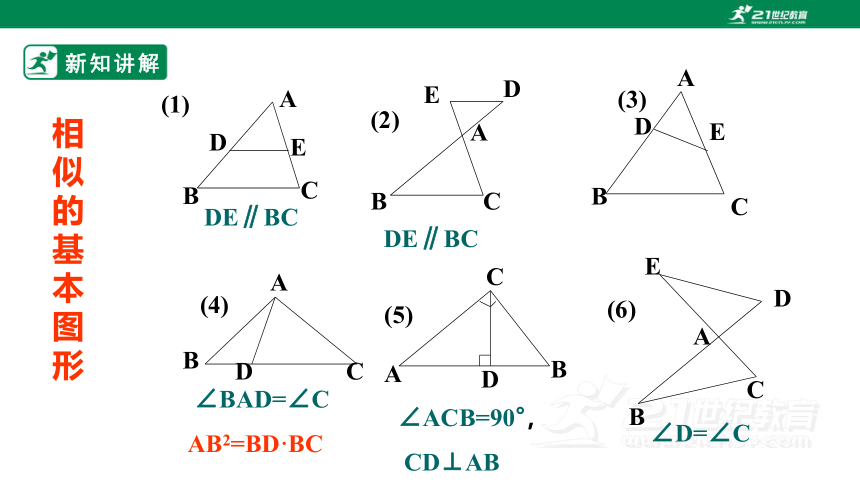
新知讲解
相
似
的
基
本
图
形
A
B
C
D
E
(1)
DE∥BC
A
B
C
D
E
DE∥BC
(2)
A
B
C
D
E
(3)
A
B
C
D
(4)
∠BAD=∠C
AB2=BD·BC
A
B
C
D
∠ACB=90°,
CD⊥AB
(5)
A
B
C
D
E
(6)
∠D=∠C
模型应用
2.如图,已知△ABC∽△ADB,点D是AC的中点,
AC=4,则AB的长为( )
A.2 B.4
C.2 D.4
【思路分析】 根据相似三角形的性质列出比例式,代入有关数据求解即可.
C
模型应用
3.已知:如图,在矩形ABCD中,点E为AD的中点,BE⊥EF,求证:△ABE∽△DEF∽△EBF.
温故知新
1、位似多边形:如果两个多边形不仅是__________,而且每对对应顶点的连线都经过同一个点,那么这样的两个多边形叫做位似多边形.
这个点叫做__________,此时的相似比叫做_______
2、利用坐标画位似图形:在平面直角坐标系中,将一样多边形每个顶点的横纵坐标都乘以同一个数K,所对应的图形和原图形____,位似中心是_________,此时的相似比为____
相似
位似中心
位似比
位似
坐标原点
K
三、位似的图形:
强化练习
4.如图,在直角坐标系中,已知点A(-3,6)、B(-9,-3)以原点O为位似中心,相似比为3:1,把△ABO缩小,则点A的对应点A′的坐标是( )
A.(-1,2) B.(-9,18)
C.(-9,18)或(9,-18) D.(-1,2)或(1,-2)
D
温故知新
物1高 :影1长 =物2高 :影2长
测高的方法
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成正比例”的原理解决。
四、相似三角形的应用一:
强化练习
5.小明要测量一座古塔的高度,从距他2米的一小块积水处C看到塔顶的倒影,已知小明的眼部离地面的高度DE是1.5米,塔底中心B到积水处C的距离是40米.求塔高AB
B
D
C
A
E
答:塔高30米.
解:∵∠DEC=∠ABC=90° ∠DCE=∠ACB
∴△DEC∽△ABC
4.
温故知新
测距的方法
测量不能到达两点间的距离,常构造相似三角形求解。
四、相似三角形的应用二:
强化练习
6.如图,为测量河流的宽度,在河对岸选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,点E在BC上,并且点A,E,D在同一直线上.若测得BE=15 m,EC=9 m,CD=16 m,则河的宽度AB等于 ( )
C
典例讲解
例2、(泰州)如图,在△ABC中,∠C=90°,AC=3,BC=4,P为BC边上的动点(与B,C不重合),PD∥AB,交AC于点D,连接AP,设CP=x,△ADP的面积为S.
(1)用含x的代数式表示AD的长;
(2)求S与x的函数表达式,并求当S随x增大
而减小时x的取值范围.
典例讲解
【解析】(1)∵PD∥AB,∴ ,
∵AC=3,BC=4,CP=x,∴ ,
∴CD= x,∴AD=AC-CD=3- x,
即AD=- x+3;
(2)根据题意得,
S= AD·CP= x(- x+3)=- (x-2)2+ ,
∴当x≥2时,S随x的增大而减小,∵0∴当S随x增大而减小时x的取值范围为2≤x<4.
典例讲解
例3、如图,已知AB为☉O直径,AC是☉O的切线,连接BC交☉O于点F,取 的中
点D,连接AD交BC于点E,过点E作EH⊥AB于H.
(1)求证:△HBE∽△ABC;
(2)若CF=4,BF=5,求AC和EH的长.
【解析】(1)∵AC是☉O的切线,∴CA⊥AB,∵EH⊥AB,
∴∠EHB=∠CAB,
∵∠EBH=∠CBA,∴△HBE∽△ABC;
(2)连接AF.∵AB是直径,∴∠AFB=90°,
∵∠C=∠C,∠CAB=∠AFC,∴△CAF∽△CBA,
典例讲解
∴CA2=CF·CB=36,
∴CA=6,AB= =3 ,
AF= =2 ,
∵ ,∴∠EAF=∠EAH,∵EF⊥AF,EH⊥AB,∴EF=EH,∵AE=AE,∴Rt△AEF≌Rt△AEH,∴AF=AH=2 ,设EF=EH=x,在Rt△EHB中,
(5-x)2=x2+( )2,∴x=2,∴EH=2.
反思:在复杂的几何图形中,构造或寻找相似的图形,转化为方程解决.
课堂总结
一 、相似三角形的应用主要有如下两个方面: 1 测高 2 测距
、测高的方法:
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长的比例”的原理解决
、测距的方法:
测量不能到达两点间的距离,常构造相似三角形求解
四、解决实际问题时(如测高、测距),
一般有以下步骤:①审题 ②构建图形
③利用相似解决问题
五、本节课内容渗透的主要数学思想和方法:
数形结合、建模、方程、函数、转化的思想等。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第4章 相似三角形
浙教版九年级上册
教学目标
1.巧用相似比求解与三角形有关的计算题.
2.利用相似的性质解题.
3.利用相似比解题.
温故知新
一、相似三角形的判定方法:
①通过定义:三边对应相等,三角相等
②平行于三角形一边的直线
③三边对应成比例(SSS)
④两边成比例且夹角相等(SAS)
⑤两角对应相等(AA)
温故知新
二、相似三角形的性质:
①对应角相等
②对应边成比例
③对应高的比等于相似比
④对应中线的比等于相似比
⑤对应角平分线的比等于相似比
周长之比等于相似比
面积之比等于相似比
典例讲解
例1、(北部湾)如图,在△ABC中,BC=120,高AD=60,正方形EFGH一边在BC上,点E,F分别在AB,AC上,AD交EF于点N,求AN的长.
【解析】设正方形EFGH的边长EF=EH=x,
∵四边形EFGH是正方形,
∴∠HEF=∠EHG=90°,EF∥BC,∴△AEF∽△ABC,
∵AD是△ABC的高,∴∠HDN=90°,
∴四边形EHDN是矩形,∴DN=EH=x,
∵△AEF∽△ABC,∴ (相似三角形对应边上的高的比等于相似比),
∵BC=120,AD=60,∴AN=60-x,∴ ,解得:x=40,∴AN=60-x=60-40=20.
强化练习
1.在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”应落在下列哪个位置处,能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”、“兵”所在位置的格点构成的三角形相似( )
A.①处 B.②处
C.③处 D.④处
B
新知讲解
相
似
的
基
本
图
形
A
B
C
D
E
(1)
DE∥BC
A
B
C
D
E
DE∥BC
(2)
A
B
C
D
E
(3)
A
B
C
D
(4)
∠BAD=∠C
AB2=BD·BC
A
B
C
D
∠ACB=90°,
CD⊥AB
(5)
A
B
C
D
E
(6)
∠D=∠C
模型应用
2.如图,已知△ABC∽△ADB,点D是AC的中点,
AC=4,则AB的长为( )
A.2 B.4
C.2 D.4
【思路分析】 根据相似三角形的性质列出比例式,代入有关数据求解即可.
C
模型应用
3.已知:如图,在矩形ABCD中,点E为AD的中点,BE⊥EF,求证:△ABE∽△DEF∽△EBF.
温故知新
1、位似多边形:如果两个多边形不仅是__________,而且每对对应顶点的连线都经过同一个点,那么这样的两个多边形叫做位似多边形.
这个点叫做__________,此时的相似比叫做_______
2、利用坐标画位似图形:在平面直角坐标系中,将一样多边形每个顶点的横纵坐标都乘以同一个数K,所对应的图形和原图形____,位似中心是_________,此时的相似比为____
相似
位似中心
位似比
位似
坐标原点
K
三、位似的图形:
强化练习
4.如图,在直角坐标系中,已知点A(-3,6)、B(-9,-3)以原点O为位似中心,相似比为3:1,把△ABO缩小,则点A的对应点A′的坐标是( )
A.(-1,2) B.(-9,18)
C.(-9,18)或(9,-18) D.(-1,2)或(1,-2)
D
温故知新
物1高 :影1长 =物2高 :影2长
测高的方法
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成正比例”的原理解决。
四、相似三角形的应用一:
强化练习
5.小明要测量一座古塔的高度,从距他2米的一小块积水处C看到塔顶的倒影,已知小明的眼部离地面的高度DE是1.5米,塔底中心B到积水处C的距离是40米.求塔高AB
B
D
C
A
E
答:塔高30米.
解:∵∠DEC=∠ABC=90° ∠DCE=∠ACB
∴△DEC∽△ABC
4.
温故知新
测距的方法
测量不能到达两点间的距离,常构造相似三角形求解。
四、相似三角形的应用二:
强化练习
6.如图,为测量河流的宽度,在河对岸选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,点E在BC上,并且点A,E,D在同一直线上.若测得BE=15 m,EC=9 m,CD=16 m,则河的宽度AB等于 ( )
C
典例讲解
例2、(泰州)如图,在△ABC中,∠C=90°,AC=3,BC=4,P为BC边上的动点(与B,C不重合),PD∥AB,交AC于点D,连接AP,设CP=x,△ADP的面积为S.
(1)用含x的代数式表示AD的长;
(2)求S与x的函数表达式,并求当S随x增大
而减小时x的取值范围.
典例讲解
【解析】(1)∵PD∥AB,∴ ,
∵AC=3,BC=4,CP=x,∴ ,
∴CD= x,∴AD=AC-CD=3- x,
即AD=- x+3;
(2)根据题意得,
S= AD·CP= x(- x+3)=- (x-2)2+ ,
∴当x≥2时,S随x的增大而减小,∵0
典例讲解
例3、如图,已知AB为☉O直径,AC是☉O的切线,连接BC交☉O于点F,取 的中
点D,连接AD交BC于点E,过点E作EH⊥AB于H.
(1)求证:△HBE∽△ABC;
(2)若CF=4,BF=5,求AC和EH的长.
【解析】(1)∵AC是☉O的切线,∴CA⊥AB,∵EH⊥AB,
∴∠EHB=∠CAB,
∵∠EBH=∠CBA,∴△HBE∽△ABC;
(2)连接AF.∵AB是直径,∴∠AFB=90°,
∵∠C=∠C,∠CAB=∠AFC,∴△CAF∽△CBA,
典例讲解
∴CA2=CF·CB=36,
∴CA=6,AB= =3 ,
AF= =2 ,
∵ ,∴∠EAF=∠EAH,∵EF⊥AF,EH⊥AB,∴EF=EH,∵AE=AE,∴Rt△AEF≌Rt△AEH,∴AF=AH=2 ,设EF=EH=x,在Rt△EHB中,
(5-x)2=x2+( )2,∴x=2,∴EH=2.
反思:在复杂的几何图形中,构造或寻找相似的图形,转化为方程解决.
课堂总结
一 、相似三角形的应用主要有如下两个方面: 1 测高 2 测距
、测高的方法:
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长的比例”的原理解决
、测距的方法:
测量不能到达两点间的距离,常构造相似三角形求解
四、解决实际问题时(如测高、测距),
一般有以下步骤:①审题 ②构建图形
③利用相似解决问题
五、本节课内容渗透的主要数学思想和方法:
数形结合、建模、方程、函数、转化的思想等。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
