1.3 二次根式的运算 (2)课件(共18张PPT)
文档属性
| 名称 | 1.3 二次根式的运算 (2)课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 949.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-12 00:00:00 | ||
图片预览





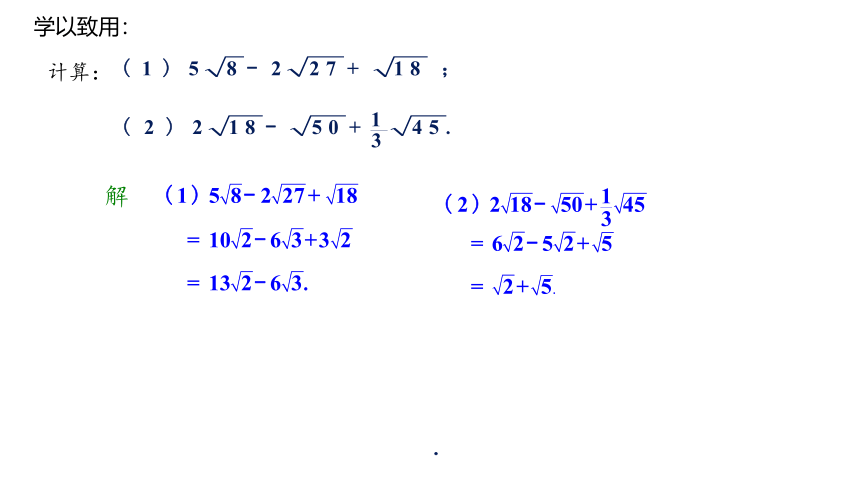

文档简介
(共18张PPT)
浙教版八下数学
1.3 二次根式的运算 (2)
温故知新:齐声朗读
(1)
=
2
.
(2)
=
2
.
(3)
=
.
(4)
=
2
.
(5)
=
2
.
(6)
=
2
.
(7)
=
.
(8)
=
2
.
(9)
=
.
=
(13)
.
=
(11)
=
(12)
=
(10)
=
(14)
=
(15)
.
.
.
.
.
根号内分数的分子、分母同乘以一个数,使分母成一个正整数的平方;
利用 (a≥0),将这个完全平方因数“开方”出来.
.
. (a b)n=an bn
积的乘方,先把积中的每一个因数分别乘方,再把所得的幂相乘
(2)2
=
12
()2
=
(2)2
=
()2
=
()2
=
()2
=
18
20
48
45
125
=
=
=
=
=
.
.
.
.
.
1.化简 (1) 3a -
3 -
=(3-
.
=
.
=(3-
.
=
.
我们把 3, - 看作系数,每一项所含的二次根
式相同( ),化简过程就和合并同类项的方法一样.
.
合并同类二次根式法:
在整式中,整式的加减实质就是合并同类项,在二次根式中,二次根式的加减运算实际上就是先把每个二次根式化成最简二次根式,再合并同类二次根式。
2. 化简
像; -; -这样,几个二次根式化成最简二次根式以后,如果被开方数相同,这几个二次根式就叫做同类二次根式 .
.
解:原式=
=
=
)
计算:
学以致用:
解
平方差公式
两数和与这两数差的积等于这两数的平方差
公式中的可以是数、单项式、多项式、二次根式
=
()2 -()2
=
3-2
=1
有理化因式:两个含有二次根式的代数式相乘,如果它们的积 不含有二次根式,就称这两个代数式互为有理化因式
分母有理化
分子、分母同乘可与分母配成平方差公式的因式
分子、分母分别计算
化为最简
例3 .计算下列各式 (1)
,
解:
=
=
=
.
计算下列各式:
学以致用:
解:
=
.
=
.
=
.
.
=
.
=
.
=
.
=
.
=7+
.
3. 计算
=
.
=
.
=
.
=
.
=
.
.
=
.
,
=
.
完全平方公式
两数和的平方,等于这两数的平方和,加上这两数积的2倍.
两数差的平方,等于这两数的平方和,减去这两数积的2倍.
.
.
.
.
公式中的可以是数、单项式、多项式、二次根式
.
学以致用:
( + )2
(2)
(3 - 5 )2
(1)
(3 )2 - 235 +( )2
=
45 - +50
=
95 -
=
( )2 - 2 +( )2
=
12- +18
=
30 -
=
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
当堂检测:
夯实基础,稳扎稳打
多项式乘多项式
多项式×多项式
单项式×多项式
单项式×单项式
+
+
+
1
2
3
4
1
2
3
4
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加
.
(1+
2.
(1
解:
原式=
2-
=
(-1
=
原式=
-
=
(1
=
3.化简
(1)
(2)
解:原式
=
=
=
=
=
(
=
(
=
=
=(1+ )(1-a)
=-(1+ )a+(1+ )
解:原式=a2-2a+1-(a2-a+ a- )
=(1+ )(1- )
=1-2=-1
连续递推,豁然开朗
4、求当 a= 时,代数式
的值.
(a-1)2-(a+)(a-1)
思维拓展,更上一层
5.计算:(-)2022 ()2021
解:(-)2021 ()()2021
.
=
.
=(-)2021 ()2021()
=【(-)()】2021()
=【()2】2021()
.
=【15-14】2021()
.
=12021()
.
浙教版八下数学
1.3 二次根式的运算 (2)
温故知新:齐声朗读
(1)
=
2
.
(2)
=
2
.
(3)
=
.
(4)
=
2
.
(5)
=
2
.
(6)
=
2
.
(7)
=
.
(8)
=
2
.
(9)
=
.
=
(13)
.
=
(11)
=
(12)
=
(10)
=
(14)
=
(15)
.
.
.
.
.
根号内分数的分子、分母同乘以一个数,使分母成一个正整数的平方;
利用 (a≥0),将这个完全平方因数“开方”出来.
.
. (a b)n=an bn
积的乘方,先把积中的每一个因数分别乘方,再把所得的幂相乘
(2)2
=
12
()2
=
(2)2
=
()2
=
()2
=
()2
=
18
20
48
45
125
=
=
=
=
=
.
.
.
.
.
1.化简 (1) 3a -
3 -
=(3-
.
=
.
=(3-
.
=
.
我们把 3, - 看作系数,每一项所含的二次根
式相同( ),化简过程就和合并同类项的方法一样.
.
合并同类二次根式法:
在整式中,整式的加减实质就是合并同类项,在二次根式中,二次根式的加减运算实际上就是先把每个二次根式化成最简二次根式,再合并同类二次根式。
2. 化简
像; -; -这样,几个二次根式化成最简二次根式以后,如果被开方数相同,这几个二次根式就叫做同类二次根式 .
.
解:原式=
=
=
)
计算:
学以致用:
解
平方差公式
两数和与这两数差的积等于这两数的平方差
公式中的可以是数、单项式、多项式、二次根式
=
()2 -()2
=
3-2
=1
有理化因式:两个含有二次根式的代数式相乘,如果它们的积 不含有二次根式,就称这两个代数式互为有理化因式
分母有理化
分子、分母同乘可与分母配成平方差公式的因式
分子、分母分别计算
化为最简
例3 .计算下列各式 (1)
,
解:
=
=
=
.
计算下列各式:
学以致用:
解:
=
.
=
.
=
.
.
=
.
=
.
=
.
=
.
=7+
.
3. 计算
=
.
=
.
=
.
=
.
=
.
.
=
.
,
=
.
完全平方公式
两数和的平方,等于这两数的平方和,加上这两数积的2倍.
两数差的平方,等于这两数的平方和,减去这两数积的2倍.
.
.
.
.
公式中的可以是数、单项式、多项式、二次根式
.
学以致用:
( + )2
(2)
(3 - 5 )2
(1)
(3 )2 - 235 +( )2
=
45 - +50
=
95 -
=
( )2 - 2 +( )2
=
12- +18
=
30 -
=
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
当堂检测:
夯实基础,稳扎稳打
多项式乘多项式
多项式×多项式
单项式×多项式
单项式×单项式
+
+
+
1
2
3
4
1
2
3
4
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加
.
(1+
2.
(1
解:
原式=
2-
=
(-1
=
原式=
-
=
(1
=
3.化简
(1)
(2)
解:原式
=
=
=
=
=
(
=
(
=
=
=(1+ )(1-a)
=-(1+ )a+(1+ )
解:原式=a2-2a+1-(a2-a+ a- )
=(1+ )(1- )
=1-2=-1
连续递推,豁然开朗
4、求当 a= 时,代数式
的值.
(a-1)2-(a+)(a-1)
思维拓展,更上一层
5.计算:(-)2022 ()2021
解:(-)2021 ()()2021
.
=
.
=(-)2021 ()2021()
=【(-)()】2021()
=【()2】2021()
.
=【15-14】2021()
.
=12021()
.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
