第五章一次函数章末复习——字母系数,参数处理;参数问题,分类讨论 课件(共11张PPT)
文档属性
| 名称 | 第五章一次函数章末复习——字母系数,参数处理;参数问题,分类讨论 课件(共11张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 176.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-12 21:14:46 | ||
图片预览




文档简介
(共11张PPT)
浙教版八上数学
第五章 一次函数 章末复习
字母问题-----分类讨论
字母系数-----参数处理------分类讨论
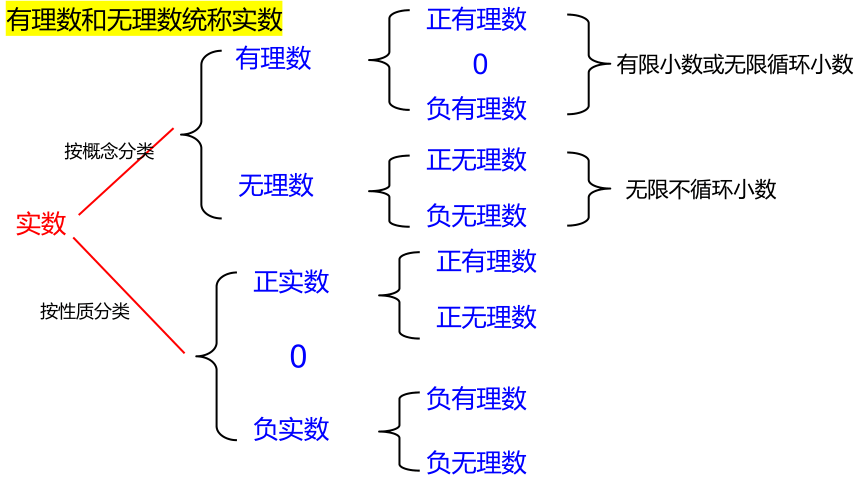
有理数
无理数
正有理数
负有理数
0
正无理数
负无理数
正实数
0
负实数
正有理数
正无理数
负有理数
负无理数
有限小数或无限循环小数
无限不循环小数
有理数和无理数统称实数
实数
按性质分类
按概念分类
在数学中,“有意义”指的是在定义限制的范围之内,符合规定、要求或限制。
(2)在实数范围内,二次根式要求被开方数不能为负数(即只能是非负数------正数或0)。如果二次根式的被开方数为负数了,就违反了在实数范围内,二次根式要求被开方数不能为负数的规定,就是“无意义”的;反之,二次根式的被开方数不是负数,就是符合规定的,就是“有意义”的。
(1)分数或分式的分母以及除数要求不能为“0”。如果分数或分式的分母以及除数为“0”了,就违反了分数或分式的规定,就是“无意义”的;反之,分数或分式的分母以及除数不是“0”就是符合规定的,就是“有意义”的。
“无意义”:做的事情没有价值,
温故知新,齐声朗读
数学中的分类讨论思想,就是当问题所给的对象不能进 统 研究时,就需要对研究对象按某个标准分类,然后对每 类分别研究得出每 类的结论,最后综合各类结果得到整个问题的解答。实质上,分类讨论是“化整为零,各个击破,再积零为整”的数学策略。
分类是 然科学乃 社会科学研究中的基本逻辑 法,是研究数学问题时经常使 的思想 法,正确地对事物进 分类,通常应从实际问题出发,选取恰当的标准,然后根据对象的属性把它们不重不漏地划分为若 类,讨论则是在所分类别的各种情况下分别进 研究。
分类三 原则:
(1)同 性原则:即不遗漏;
(2)互斥性原则:即不重复;
(3)层次性原则:即按同 个标准来分类,逐级进 ,层次分明
分类讨论思想是一种重要的数学思想方法,其基本思路是将一个较复杂的数学问题分解 (或分割)成若干个基础性问题,通过对基础性问题的解答来实现解决原问题的思想策略。
解答数学时,有时会涉及很多情况,并且要对每种情况加以说明,逐个求解,得出结论。这就会涉及分类讨论思想。
分类讨论思想的核心是:化整为零,积零为整。
讨论的根本:不确定性
什么时候需要化整为零?
含参数的函数、方程、不等式等问题、
几何中由于某个点的位置不确定或图形不确定问题……
1. 解关于x的方程: ax=b
解:
当a0时,
.
此方程有唯一解 x=
.
当a=0时,
.
①
当0时,
0x=b (0)
.
此方程无解
②
当b=0时,
.
0x=0
.
此方程有无数解
a、b不确定:a、b可以这样,a、b也可以那样,a、b还可以……
2. 解关于x的不等式: ax >b
解:
当a>0时,
.
此不等式解为: x
.
当a=0时,
.
①
当0时,
0x>b (0)
.
此不等式无解
②
当b=0时,
.
0x>0
.
此不等式无解
③当b<0时
0x>b (0)
.
此不等式有解:全体实数
此不等式解为: x
.
当a<0时,
.
a、b不确定:a、b可以这样,a、b也可以那样,a、b还可以……
分析:
当x-1>0时,
.
是正数
.
3. 关于x的分式:
.
当x-1=0时,
.
在实数范围内无意义
.
当x-1<0时
是负数
.
分析:
当x-1>0时,
.
是正数
当x-1=0时,
.
是 0
当x-1<0时
在实数范围内无意义
有意义,存在
有意义,存在
分母不确定:分母可以这样,分母也可以那样,分母还可以……
被开方数不确定:被开方数可以这样,被开方数也可以那样,被开方数还可以……
4. 关于x的二次根式:
.
5.画函数y=kx+1的图像,b=1
x
y
0
1
x
y
0
1
x
y
0
1
当k>0时,呈“ ”
直线y=kx+1
直线y=kx+1
直线y=1
当k<0时,呈“ ”
当k=0时,呈“ ”
k不确定:k可以这样,k也可以那样,k还可以……
b确定
与y轴交点位置确定
6.画函数y=x+b的图像,k=1
x
y
0
b
x
y
0
b
x
y
0
当b>0时,交点:y轴正半轴
直线y=x+b
直线y=x+b
直线y=x
当b<0时,交点:y轴负半轴
当b=0时,交点:原点
b不确定:b可以这样,b也可以那样,b还可以……
7.化简 m-2 + m+3
O
1
2
3
4
5
-1
-2
-4
-3
-5
m
A
B
(1)m-2=0 ,m1=2
(2)m+3=0 , m2=-3
两个0点:
两个正负分界点: A 、 B
原式=(m-2)+(m+3)
= m-2+m+3
=2m+1
当-3m
.
原式=[-(m-2)]+(m+3)
= -m+2+m+3
=5
原式=[-(m-2)]+[-(m+3)]
= -m+2-m-3
=-2m-1
m
m
m
水平线段长度=右 - 左
m+3 =
m-(-3)
m不确定:可以这样,也可以那样
当m
.
当m
.
浙教版八上数学
第五章 一次函数 章末复习
字母问题-----分类讨论
字母系数-----参数处理------分类讨论
有理数
无理数
正有理数
负有理数
0
正无理数
负无理数
正实数
0
负实数
正有理数
正无理数
负有理数
负无理数
有限小数或无限循环小数
无限不循环小数
有理数和无理数统称实数
实数
按性质分类
按概念分类
在数学中,“有意义”指的是在定义限制的范围之内,符合规定、要求或限制。
(2)在实数范围内,二次根式要求被开方数不能为负数(即只能是非负数------正数或0)。如果二次根式的被开方数为负数了,就违反了在实数范围内,二次根式要求被开方数不能为负数的规定,就是“无意义”的;反之,二次根式的被开方数不是负数,就是符合规定的,就是“有意义”的。
(1)分数或分式的分母以及除数要求不能为“0”。如果分数或分式的分母以及除数为“0”了,就违反了分数或分式的规定,就是“无意义”的;反之,分数或分式的分母以及除数不是“0”就是符合规定的,就是“有意义”的。
“无意义”:做的事情没有价值,
温故知新,齐声朗读
数学中的分类讨论思想,就是当问题所给的对象不能进 统 研究时,就需要对研究对象按某个标准分类,然后对每 类分别研究得出每 类的结论,最后综合各类结果得到整个问题的解答。实质上,分类讨论是“化整为零,各个击破,再积零为整”的数学策略。
分类是 然科学乃 社会科学研究中的基本逻辑 法,是研究数学问题时经常使 的思想 法,正确地对事物进 分类,通常应从实际问题出发,选取恰当的标准,然后根据对象的属性把它们不重不漏地划分为若 类,讨论则是在所分类别的各种情况下分别进 研究。
分类三 原则:
(1)同 性原则:即不遗漏;
(2)互斥性原则:即不重复;
(3)层次性原则:即按同 个标准来分类,逐级进 ,层次分明
分类讨论思想是一种重要的数学思想方法,其基本思路是将一个较复杂的数学问题分解 (或分割)成若干个基础性问题,通过对基础性问题的解答来实现解决原问题的思想策略。
解答数学时,有时会涉及很多情况,并且要对每种情况加以说明,逐个求解,得出结论。这就会涉及分类讨论思想。
分类讨论思想的核心是:化整为零,积零为整。
讨论的根本:不确定性
什么时候需要化整为零?
含参数的函数、方程、不等式等问题、
几何中由于某个点的位置不确定或图形不确定问题……
1. 解关于x的方程: ax=b
解:
当a0时,
.
此方程有唯一解 x=
.
当a=0时,
.
①
当0时,
0x=b (0)
.
此方程无解
②
当b=0时,
.
0x=0
.
此方程有无数解
a、b不确定:a、b可以这样,a、b也可以那样,a、b还可以……
2. 解关于x的不等式: ax >b
解:
当a>0时,
.
此不等式解为: x
.
当a=0时,
.
①
当0时,
0x>b (0)
.
此不等式无解
②
当b=0时,
.
0x>0
.
此不等式无解
③当b<0时
0x>b (0)
.
此不等式有解:全体实数
此不等式解为: x
.
当a<0时,
.
a、b不确定:a、b可以这样,a、b也可以那样,a、b还可以……
分析:
当x-1>0时,
.
是正数
.
3. 关于x的分式:
.
当x-1=0时,
.
在实数范围内无意义
.
当x-1<0时
是负数
.
分析:
当x-1>0时,
.
是正数
当x-1=0时,
.
是 0
当x-1<0时
在实数范围内无意义
有意义,存在
有意义,存在
分母不确定:分母可以这样,分母也可以那样,分母还可以……
被开方数不确定:被开方数可以这样,被开方数也可以那样,被开方数还可以……
4. 关于x的二次根式:
.
5.画函数y=kx+1的图像,b=1
x
y
0
1
x
y
0
1
x
y
0
1
当k>0时,呈“ ”
直线y=kx+1
直线y=kx+1
直线y=1
当k<0时,呈“ ”
当k=0时,呈“ ”
k不确定:k可以这样,k也可以那样,k还可以……
b确定
与y轴交点位置确定
6.画函数y=x+b的图像,k=1
x
y
0
b
x
y
0
b
x
y
0
当b>0时,交点:y轴正半轴
直线y=x+b
直线y=x+b
直线y=x
当b<0时,交点:y轴负半轴
当b=0时,交点:原点
b不确定:b可以这样,b也可以那样,b还可以……
7.化简 m-2 + m+3
O
1
2
3
4
5
-1
-2
-4
-3
-5
m
A
B
(1)m-2=0 ,m1=2
(2)m+3=0 , m2=-3
两个0点:
两个正负分界点: A 、 B
原式=(m-2)+(m+3)
= m-2+m+3
=2m+1
当-3m
.
原式=[-(m-2)]+(m+3)
= -m+2+m+3
=5
原式=[-(m-2)]+[-(m+3)]
= -m+2-m-3
=-2m-1
m
m
m
水平线段长度=右 - 左
m+3 =
m-(-3)
m不确定:可以这样,也可以那样
当m
.
当m
.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
