2.3.2等腰三角形的性质定理

课件10张PPT。2.3.2等腰三角形的性质雷甸中学 姜俊卿
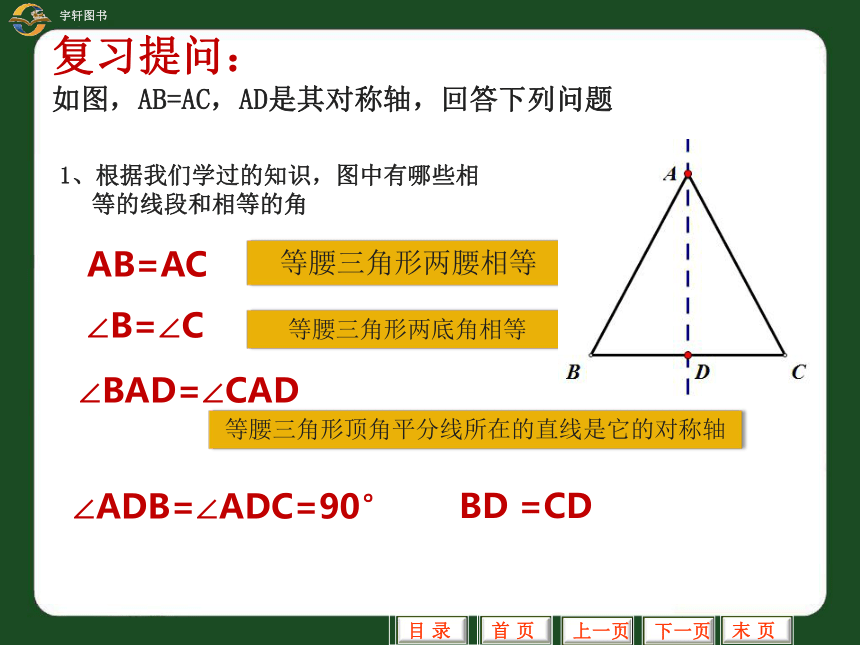
QQ:85286874复习提问：如图，AB=AC，AD是其对称轴，回答下列问题1、根据我们学过的知识，图中有哪些相等的线段和相等的角
等腰三角形两底角相等等腰三角形两腰相等AB=AC∠B=∠C∠BAD=∠CAD等腰三角形顶角平分线所在的直线是它的对称轴∠ADB=∠ADC=90°BD =CD 新知识：如图，AB=AC，AD是其对称轴，回答下列问题2、线段AD除了是△ABC的角平分线之外，它还是△ABC的哪种特殊线段？
∠ADB=∠ADC=90°BD =CD 线段AD∠BAC的平分线BC边上的中线BC边上的高互相重合3、完成下面的填空，总结你所发现的规律
等腰三角形中_____________、_________ __和___________ 互相重合
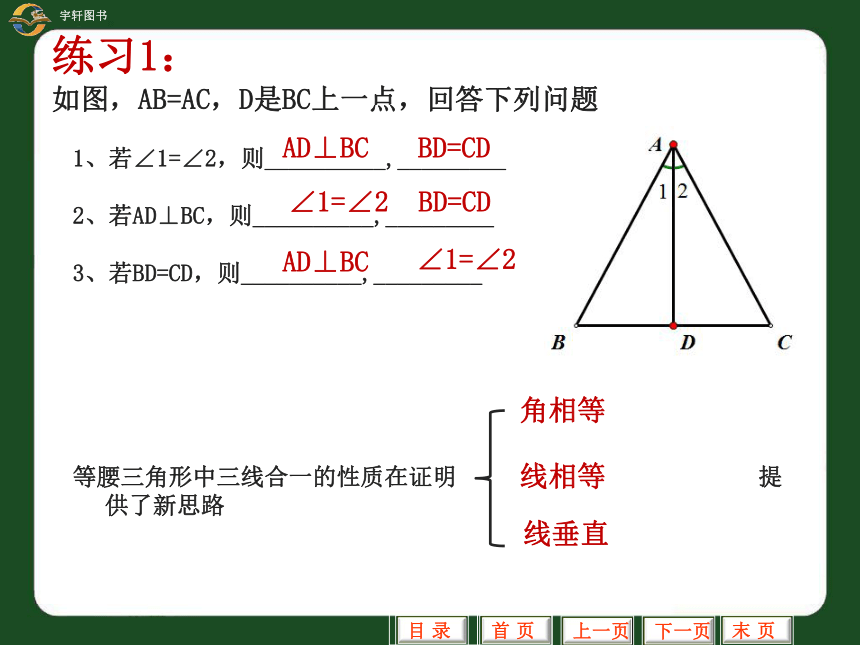
顶角平分线底边上的中线底边上的高练习1：如图，AB=AC，D是BC上一点，回答下列问题1、若∠1=∠2，则__________,_________
2、若AD⊥BC，则__________,_________
3、若BD=CD，则__________,_________∠1=∠2AD⊥BCBD=CD∠1=∠2AD⊥BCBD=CD等腰三角形中三线合一的性质在证明 提供了新思路
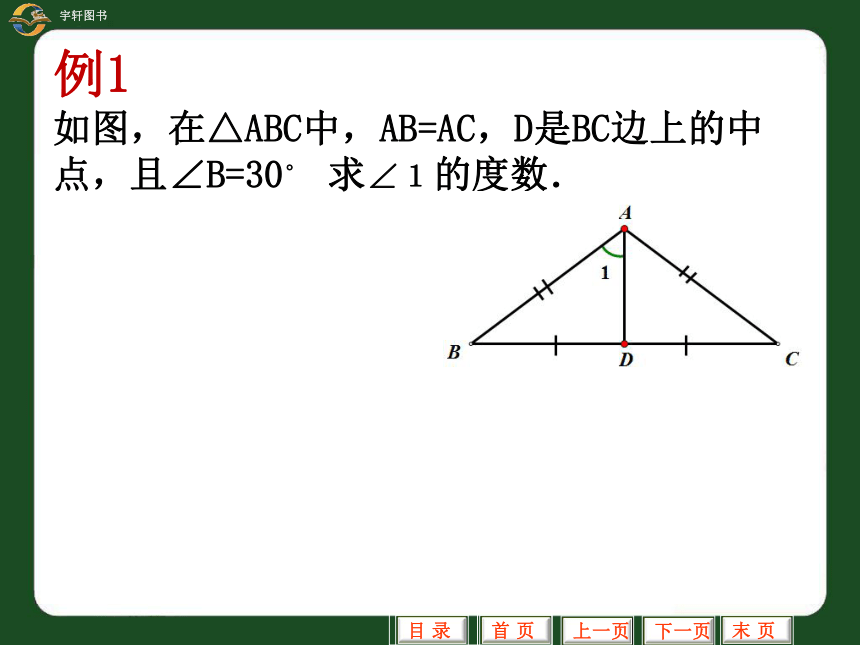
角相等线相等线垂直例1如图，在△ABC中，AB=AC，D是BC边上的中点，且∠B=30。 求∠１的度数． 例2：已知：如图，AD平分∠BAC，∠ADB=∠ADC求证：AD⊥BCE1 2证明：延长AD交BC于点EAD平分∠BAC∠1=∠2AD=AD∠ADB=∠ADC△ABD≌
△ACDAB=ACAE平分∠BACAE⊥BC即 AD⊥BC练习2：下列命题哪些是真命题，哪些是假命题？1、如右图，AP⊥BC，则BP=CP
2、如右图，若AB=AC，AQ=BQ，
则CQ平分∠ACB
3、如右图，若AP⊥BC，则△APB≌△APC
4、等腰三角形底边上的高所在的直线
是它的对称轴
5、等腰三角形顶角的平分线 是 其底边的中垂线
假命题假命题真命题真命题真命题例.3已知线段a,h用直尺和圆规作腰三角形ABC，使①底边BC=a， ②底边BC上的高线等于长为h.反思小结 这节课你有什么收获？巩固案配图