第5章 一次函数单元检测卷(含解析)

中小学教育资源及组卷应用平台
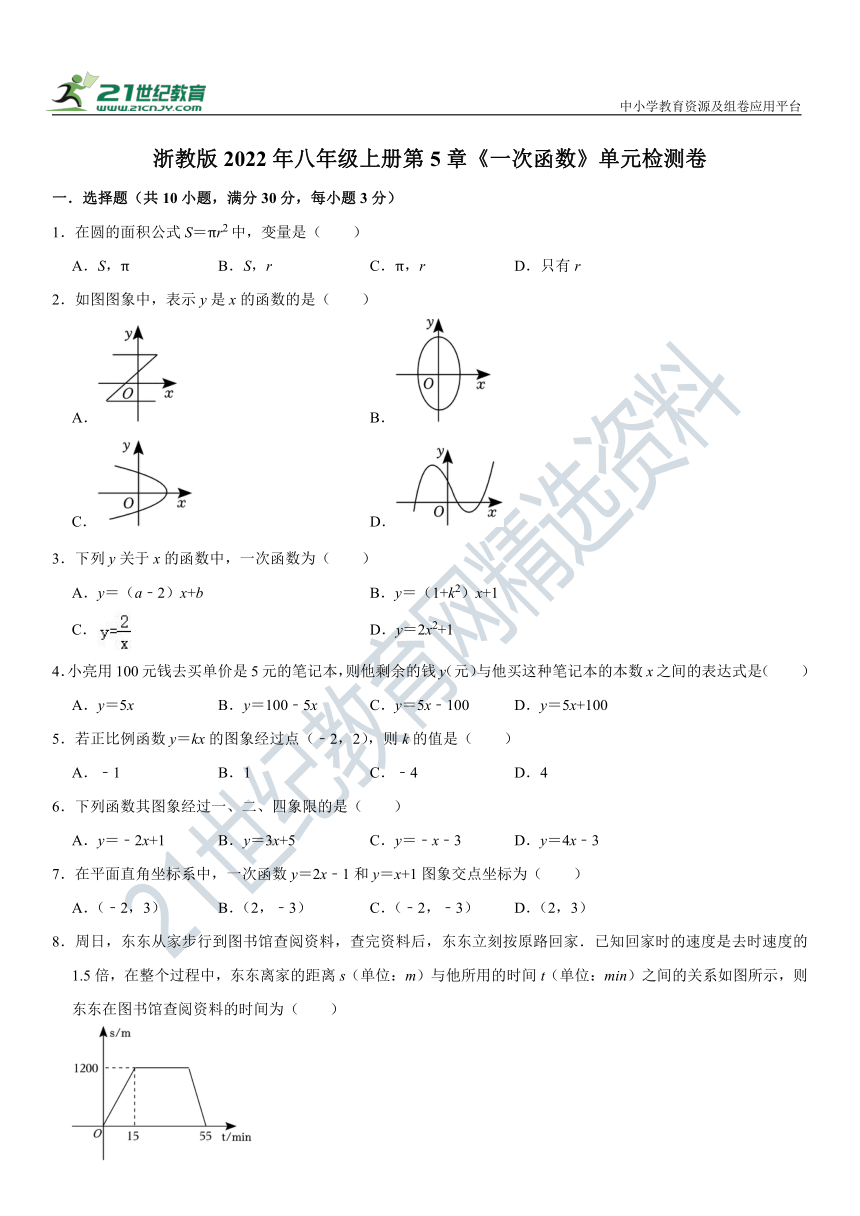
浙教版2022年八年级上册第5章《一次函数》单元检测卷
一．选择题（共10小题，满分30分，每小题3分）
1．在圆的面积公式S＝πr2中，变量是（　　）
A．S，π B．S，r C．π，r D．只有r
2．如图图象中，表示y是x的函数的是（　　）
A． B．
C． D．
3．下列y关于x的函数中，一次函数为（　　）
A．y＝（a﹣2）x+b B．y＝（1+k2）x+1
C． D．y＝2x2+1
4．小亮用100元钱去买单价是5元的笔记本，则他剩余的钱y（元）与他买这种笔记本的本数x之间的表达式是（　　）
A．y＝5x B．y＝100﹣5x C．y＝5x﹣100 D．y＝5x+100
5．若正比例函数y＝kx的图象经过点（﹣2，2），则k的值是（　　）
A．﹣1 B．1 C．﹣4 D．4
6．下列函数其图象经过一、二、四象限的是（　　）
A．y＝﹣2x+1 B．y＝3x+5 C．y＝﹣x﹣3 D．y＝4x﹣3
7．在平面直角坐标系中，一次函数y＝2x﹣1和y＝x+1图象交点坐标为（　　）
A．（﹣2，3） B．（2，﹣3） C．（﹣2，﹣3） D．（2，3）
8．周日，东东从家步行到图书馆查阅资料，查完资料后，东东立刻按原路回家．已知回家时的速度是去时速度的1.5倍，在整个过程中，东东离家的距离s（单位：m）与他所用的时间t（单位：min）之间的关系如图所示，则东东在图书馆查阅资料的时间为（　　）
A．55min B．40min C．30min D．25min
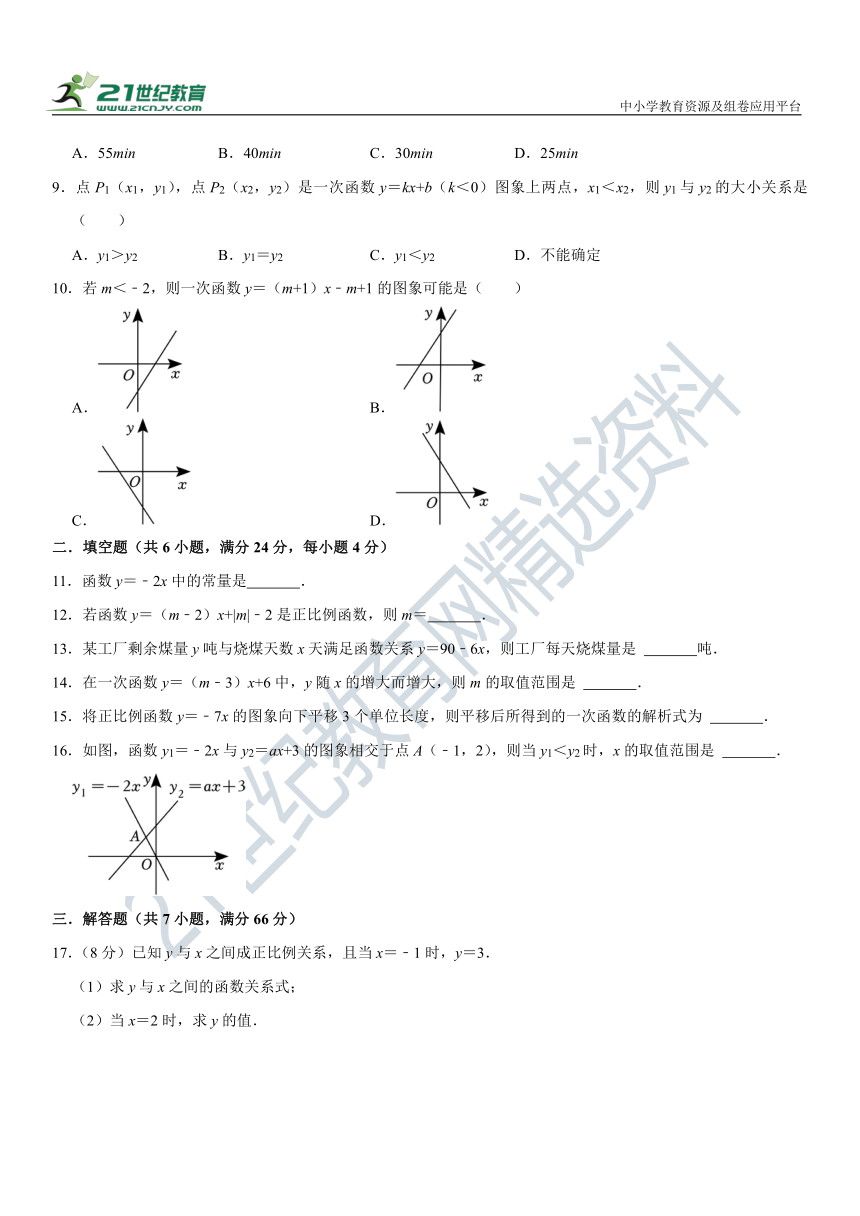
9．点P1（x1，y1），点P2（x2，y2）是一次函数y＝kx+b（k＜0）图象上两点，x1＜x2，则y1与y2的大小关系是（　　）
A．y1＞y2 B．y1＝y2 C．y1＜y2 D．不能确定
10．若m＜﹣2，则一次函数y＝（m+1）x﹣m+1的图象可能是（　　）
A． B．
C． D．
二．填空题（共6小题，满分24分，每小题4分）
11．函数y＝﹣2x中的常量是　 　．
12．若函数y＝（m﹣2）x+|m|﹣2是正比例函数，则m＝　 　．
13．某工厂剩余煤量y吨与烧煤天数x天满足函数关系y＝90﹣6x，则工厂每天烧煤量是 　 　吨．
14．在一次函数y＝（m﹣3）x+6中，y随x的增大而增大，则m的取值范围是 　 　．
15．将正比例函数y＝﹣7x的图象向下平移3个单位长度，则平移后所得到的一次函数的解析式为 　 　．
16．如图，函数y1＝﹣2x与y2＝ax+3的图象相交于点A（﹣1，2），则当y1＜y2时，x的取值范围是 　 　．
三．解答题（共7小题，满分66分）
17．（8分）已知y与x之间成正比例关系，且当x＝﹣1时，y＝3．
（1）求y与x之间的函数关系式；
（2）当x＝2时，求y的值．
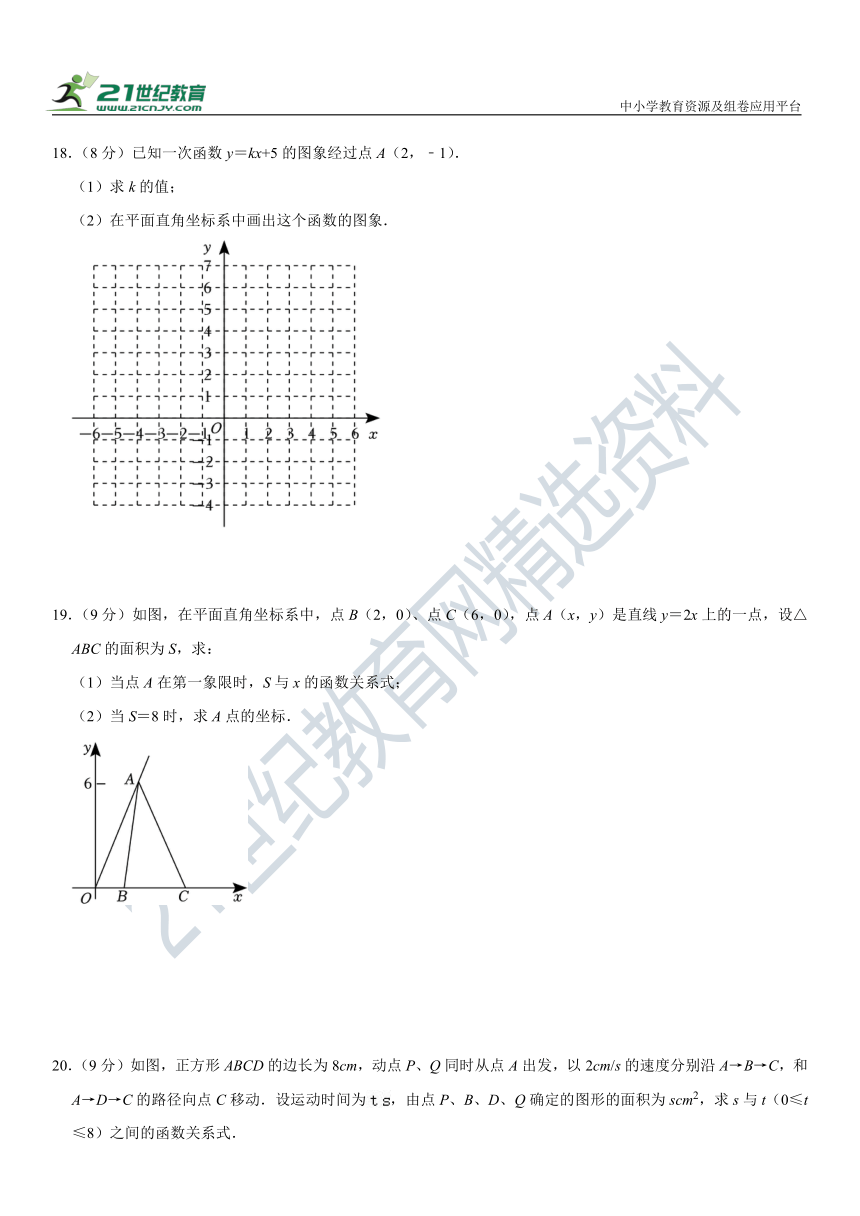
18．（8分）已知一次函数y＝kx+5的图象经过点A（2，﹣1）．
（1）求k的值；
（2）在平面直角坐标系中画出这个函数的图象．
19．（9分）如图，在平面直角坐标系中，点B（2，0）、点C（6，0），点A（x，y）是直线y＝2x上的一点，设△ABC的面积为S，求：
（1）当点A在第一象限时，S与x的函数关系式；
（2）当S＝8时，求A点的坐标．
20．（9分）如图，正方形ABCD的边长为8cm，动点P、Q同时从点A出发，以2cm/s的速度分别沿A→B→C，和A→D→C的路径向点C移动．设运动时间为，由点P、B、D、Q确定的图形的面积为scm2，求s与t（0≤t≤8）之间的函数关系式．
21．（10分）李老师一家去离家200千米的某地自驾游，周六上午8点整出发．下面是他们离家的距离y（千米）与汽车行驶时间x（千米）之间的函数图象．
（1）求他们出发半小时时，离家多少千米？
（2）出发1小时后，在服务区等另一家人一同前往，等到后以每小时80千米的速度直达目的地；求等候的时间及直线BC的解析式；
（3）上午11点时，离目的地还有多少千米？
22．（10分）如图，已知直线y＝﹣x+2与x轴，y轴分别交于点A和点B，另一直线y＝kx+b（k≠0）经过C（1，0），且把△AOB分成两部分．
（1）若直线y＝kx+b也经过点B，试说明△BOC与△ABC的面积相等；
（2）若△AOB被分成的两部分面积比为1：5，求k和b的值．
23．（12分）如图1，直线AB交x轴于点A（a，0），交y轴于点B（0，b），且a，b满足（a+b）2+（a﹣4）2＝0．
（1）如图1，若C的坐标为（﹣1，0），且AH⊥BC于点H，AH交OB于点P，求点P的坐标；
（2）如图2，连接OH，求证：∠AHO＝45°；
（3）如图3，若点D为AB的中点，点M为y轴正半轴上一动点，连接MD，过D作DN⊥DM交x轴于N点，当M点在y轴正半轴上运动的过程中，式子S△BDM﹣S△ADN的值是否发生改变，如发生改变，求出该式子的值的变化范围；若不改变，求该式子的值．
浙教版2022年八年级上册第5章《一次函数》单元检测卷
参考答案
一．选择题（共10小题，满分30分，每小题3分）
1．【解答】解：根据常量和变量的定义得S、R是变量，π是常量．
故选：B．
2．【解答】解：A、B、C中对于自变量x的每一个值，因变量y不是都有唯一的值与它对应，所以不能表示y是x的函数；
D选项中对于自变量x的每一个值，因变量y都有唯一的值与它对应，所以能表示y是x的函数．
故选：D．
3．【解答】解：A．当a＝0时，y＝（a﹣2）x+b不是一次函数，故本选项不符合题意；
B．y＝（1+k2）x+1是一次函数，故本选项符合题意；
C．等式的右边是分式，不是整式，不是一次函数，故本选项不符合题意；
D．y＝2x2+1是二次函数，不是一次函数，故本选项不符合题意；
故选：B．
4．【解答】解：∵小亮用100元钱去买单价是5元的笔记本，
∴买这种笔记本的本数x花去的钱为：5x，
∴剩余的钱为：100﹣5x，
∴他剩余的钱（y元）与他买这种笔记本的本数x之间的函数关系式是：y＝100﹣5x，
故选：B．
5．【解答】解：∵正比例函数y＝kx的图象经过点（﹣2，2），
∴2＝﹣2k，
解得：k＝﹣1．
故选：A．
6．【解答】解：A选项，图象过第一、二、四象限，符合题意；
B选项，图象过第一、二、三象限，不符合题意；
C选项，图象过第二、三、四象限，不符合题意；
D选项，图象过第一、三、四象限，不符合题意；
故选：A．
7．【解答】解：联立解得：，
∴函数y＝2x﹣1与y＝x+1的图象的交点坐标为（2，3）．
故选：D．
8．【解答】解：根据图象可知，
东东从家步行到图书馆的速度为：
＝80（m/min），
∵回家时的速度是去时速度的1.5倍，
∴回家时的速度为：
1.5×80＝120（m/min），
则回家所用的时间为：
＝10（m/min），
∴东东在图书馆查阅资料的时间为：
55﹣（15+10）＝30（min），
故选：C．
9．【解答】解：∵一次函数y＝kx+b（k＜0），
∴此函数中y随x的增大而减小，
∵x1＜x2，
∴y1＞y2．
故选：A．
10．【解答】解：∵m＜﹣2，
∴m+1＜0，﹣m+1＞0，
∴一次函数y＝（m+1）x﹣m+1的图象经过一二四象限．
故选：D．
二．填空题（共6小题，满分24分，每小题4分）
11．【解答】解：y＝﹣2x中的常量是﹣2，
故答案为：﹣2．
12．【解答】解：由题意得：
|m|﹣2＝0且m﹣2≠0，
∴m＝±2且m≠2，
∴m＝﹣2，
故答案为：﹣2．
13．【解答】解：某工厂剩余煤量y吨与烧煤天数x天满足函数关系y＝90﹣6x，则工厂每天烧煤量是6吨，
故答案为：6．
14．【解答】解：根据题意得：m﹣3＞0，
解得m＞3．
故答案为：m＞3．
15．【解答】解：将正比例函数y＝﹣7x的图象向下平移3个单位长度，所得的函数解析式为y＝﹣7x﹣3．
故答案为：y＝﹣7x﹣3．
16．【解答】解：∵函数y1＝﹣2x与y2＝ax+3的图象相交于点A（﹣1，2），
∴当y1＜y2时，x的取值范围是x＞﹣1．
故答案为：x＞﹣1．
三．解答题（共7小题，满分66分）
17．【解答】解（1）设y＝kx（k≠0），把x＝﹣1，y＝3代入y＝kx，
得k＝﹣3，
所以y＝﹣3x．
（2）把x＝2代入y＝﹣3x，
得y＝﹣3×2＝﹣6．
18．【解答】解：（1）把点A（2，﹣1）代入一次函数y＝kx+5，得﹣1＝2k+5，
解得k＝﹣3．
（2）当x＝0时，y＝5，
可知直线与y轴交点为（0，5），
作过B、C的直线可得如图所示直线，即为所求．
19．【解答】解：（1）∵B（2，0）、C（6，0），
∴BC＝6﹣2＝4，
∵第一象限内的点A（x，y）是直线y＝2x上一点，
∴△PAO的面积为S＝×4×2x＝4x；
（2）S＝4x＝8，解得x＝2，
∴y＝2×2＝4，
∴A点的坐标（2，4）．
20．【解答】解：①0≤t≤4时，
∵正方形的边长为8cm，
∴y＝S△ABD﹣S△APQ，
＝×8×8﹣ 2t 2t，
＝﹣2t2+32，
②4≤t≤8时，
y＝S△BCD﹣S△CPQ，
＝×8×8﹣ （16﹣2t） （16﹣2t），
＝﹣2t2+32t﹣96．
综上所述，S＝．
21．【解答】解：（1）由图象知，李老师从家到服务区时的速度为＝60千米/小时，
∴李老师出发半小时离家的距离为：60×0.5＝30（千米），
答：他们出发半小时时，离家30千米；
（2）李老师一家从服务区B到C地所用时间为：（100﹣60）÷80＝0.5（小时），
∴李老师一家在服务区等了2﹣1﹣0.5＝0.5（小时）；
设线段BC的函数表达式为y＝kx+b，
因为B（1.5，60），C（2，100）在BC上，
∴，
解得，
∴直线BC的解析式为y＝80x﹣60；
（3）上午11点时，即x＝3时，y＝80×3﹣60＝180，
∴200﹣180＝20（千米），
答：上午11点时，离目的地还有20千米．
22．【解答】解：（1）在y＝﹣x+2中，令y＝0，则﹣x+2＝0，
解得x＝2，
∴A（2，0），
∴OA＝2，
∵C（1，0），
∴OC＝1，
∴点C是线段OA的中点，
∴△BOC与△ABC的面积相等；
（2）∵S△AOB＝×2×2＝2，
∵△AOB被分成的两部分面积比为1：5，那么直线y＝kx+b（k≠0）与y轴或AB交点的纵坐标就应该是：2×2×＝，
①当y＝kx+b（k≠0）与直线y＝﹣x+2相交时，交点为D，如图（2）所示，
当y＝时，直线y＝﹣x+2与y＝kx+b（k≠0）的交点D的横坐标就应该是﹣x+2＝，
∴x＝，
即交点D的坐标为（ ，），
又根据C点的坐标为（1，0），可得：
∴，
②当y＝kx+b（k≠0）与y轴相交时，交点为E，如图（3）所示，
∴交点E的坐标就应该是（0，），又有C点的坐标（1，0），可得：
，
∴，
综上所述，k＝2，b＝﹣2或k＝﹣，b＝．
23．【解答】解：（1）如图1，
∵（a+b）2+（a﹣4）2＝0．
∴a+b＝0，a﹣4＝0，
∴a＝4，b＝﹣4，
则OA＝OB＝4．
∵AH⊥BC即∠AHC＝90°，∠COB＝90°
∴∠HAC+∠ACH＝∠OBC+∠OCB＝90°，
∴∠HAC＝∠OBC．
在△OAP与△OBC中，
，
∴△OAP≌△OBC（ASA），
∴OP＝OC＝1，
则P（0，﹣1）；
（2）过O分别作OM⊥CB于M点，作ON⊥HA于N点，如图2．
在四边形OMHN中，∠MON＝360°﹣3×90°＝90°，
∴∠COM＝∠PON＝90°﹣∠MOP．
在△COM与△PON中，
，
∴△COM≌△PON（AAS），
∴OM＝ON．
∵OM⊥CB，ON⊥HA，
∴HO平分∠CHA，
∴∠OHP＝∠CHA＝45°；
（3）S△BDM﹣S△ADN的值不发生改变，等于4．
理由如下：
连接OD，如图3．
∵∠AOB＝90°，OA＝OB，D为AB的中点，
∴OD⊥AB，∠BOD＝∠AOD＝45°，OD＝DA＝BD，
∴∠OAD＝45°，∠MOD＝90°+45°＝135°，
∴∠DAN＝135°＝∠MOD．
∵MD⊥ND即∠MDN＝90°，
∴∠MDO＝∠NDA＝90°﹣∠MDA．
在△ODM与△ADN中，
，
∴△ODM≌△ADN（ASA），
∴S△ODM＝S△ADN，
∴S△BDM﹣S△ADN
＝S△BDM﹣S△ODM
＝S△BOD
＝S△AOB
＝×AO BO
＝××4×4
＝4．