第5章 一次函数单元测试卷(困难 含答案)
文档属性
| 名称 | 第5章 一次函数单元测试卷(困难 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 350.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-13 17:40:40 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
浙教版初中数学八年级上册第五单元《一次函数》单元测试卷
考试范围:第五章;考试时间:120分钟;总分:120分
学校:___________姓名:___________班级:___________考号:___________
第I卷(选择题)
一、选择题(本大题共12小题,共36分。在每小题列出的选项中,选出符合题目的一项)
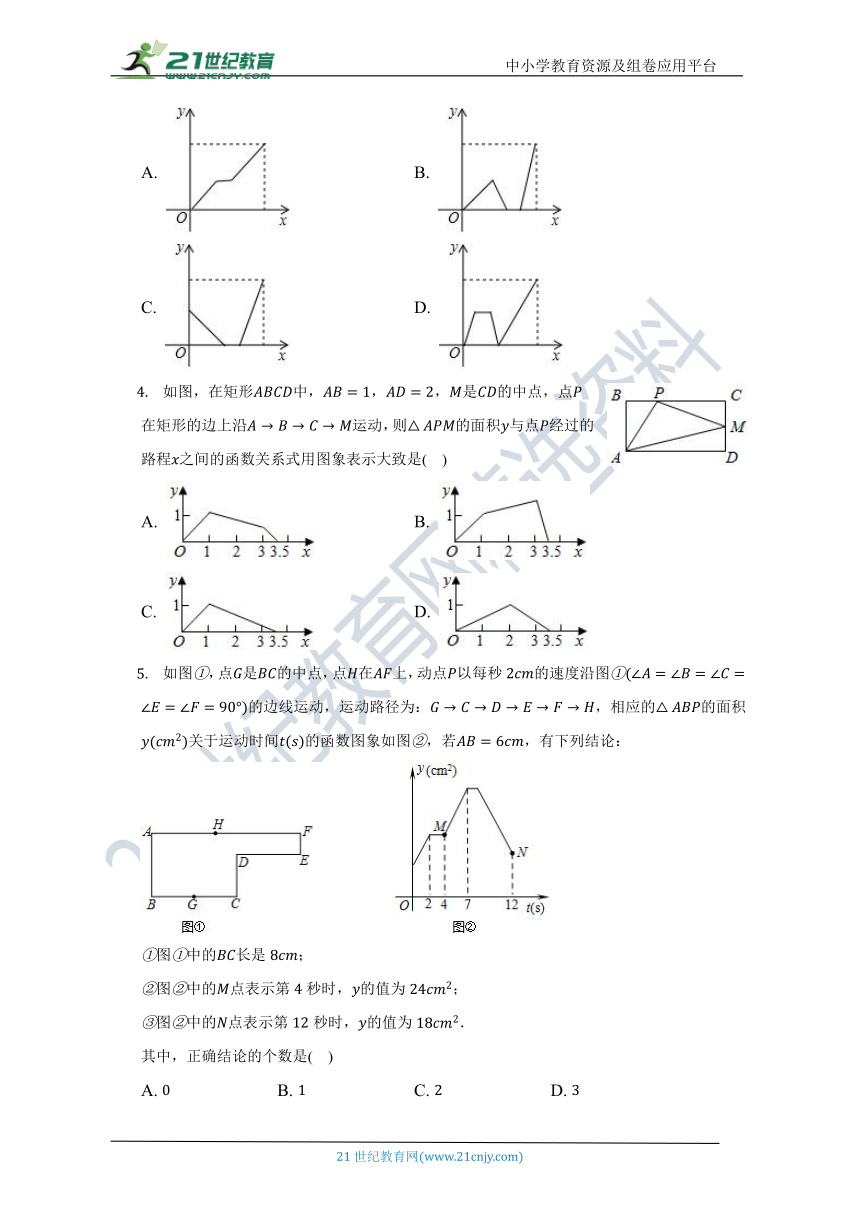
甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从地到地,乙驾车从地到地,他们分别以不同的速度匀速行驶.已知甲先出发分钟后,乙才出发,在整个过程中,甲、乙两人的距离千米与甲出发的时间分之间的关系如图所示,当乙到达终点时,甲还需分钟到达终点.( )
A. B. C. D.
明明在爬山的活动中,先快速跑步上山,累了停下来休息了一段时间后,再慢慢爬到山顶,下图中能大致反映明明离山顶的路程与登山时间的关系的是( )
A. B.
C. D.
早上,小明从家里步行去学校,出发一段时间后,小明妈妈发现小明的作业本落在家里,便带上作业本骑车追赶,途中追上小明两人稍作停留,妈妈骑车返回,小明继续步行前往学校,两人同时到达.设小明在途的时间为,两人之间的距离为,则下列选项中的图象能大致反映与之间关系的是( )
A. B.
C. D.
如图,在矩形中,,,是的中点,点在矩形的边上沿运动,则的面积与点经过的路程之间的函数关系式用图象表示大致是( )
A. B.
C. D.
如图,点是的中点,点在上,动点以每秒的速度沿图的边线运动,运动路径为:,相应的的面积关于运动时间的函数图象如图,若,有下列结论:
图中的长是;
图中的点表示第秒时,的值为;
图中的点表示第秒时,的值为.
其中,正确结论的个数是( )
A. B. C. D.
如图,已知在中,,点沿自向运动,作于,于,则的值与的长之间的函数图象大致是( )
A. B.
C. D.
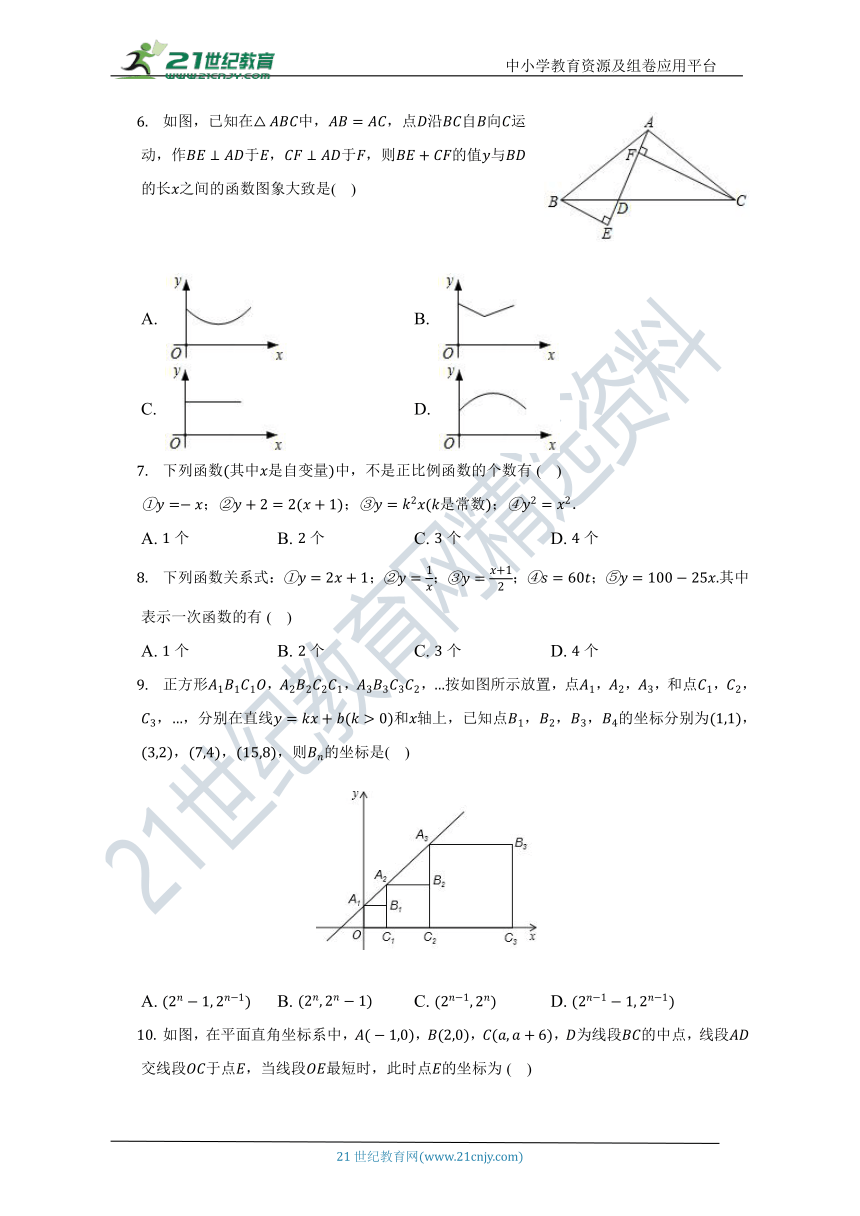
下列函数其中是自变量中,不是正比例函数的个数有( )
;;是常数;.
A. 个 B. 个 C. 个 D. 个
下列函数关系式:;;;;其中表示一次函数的有( )
A. 个 B. 个 C. 个 D. 个
正方形,,,按如图所示放置,点,,,和点,,,,分别在直线和轴上,已知点,,,的坐标分别为,,,,则的坐标是( )
A. B. C. D.
如图,在平面直角坐标系中,,,,为线段的中点,线段交线段于点,当线段最短时,此时点的坐标为( )
A. B. C. D.
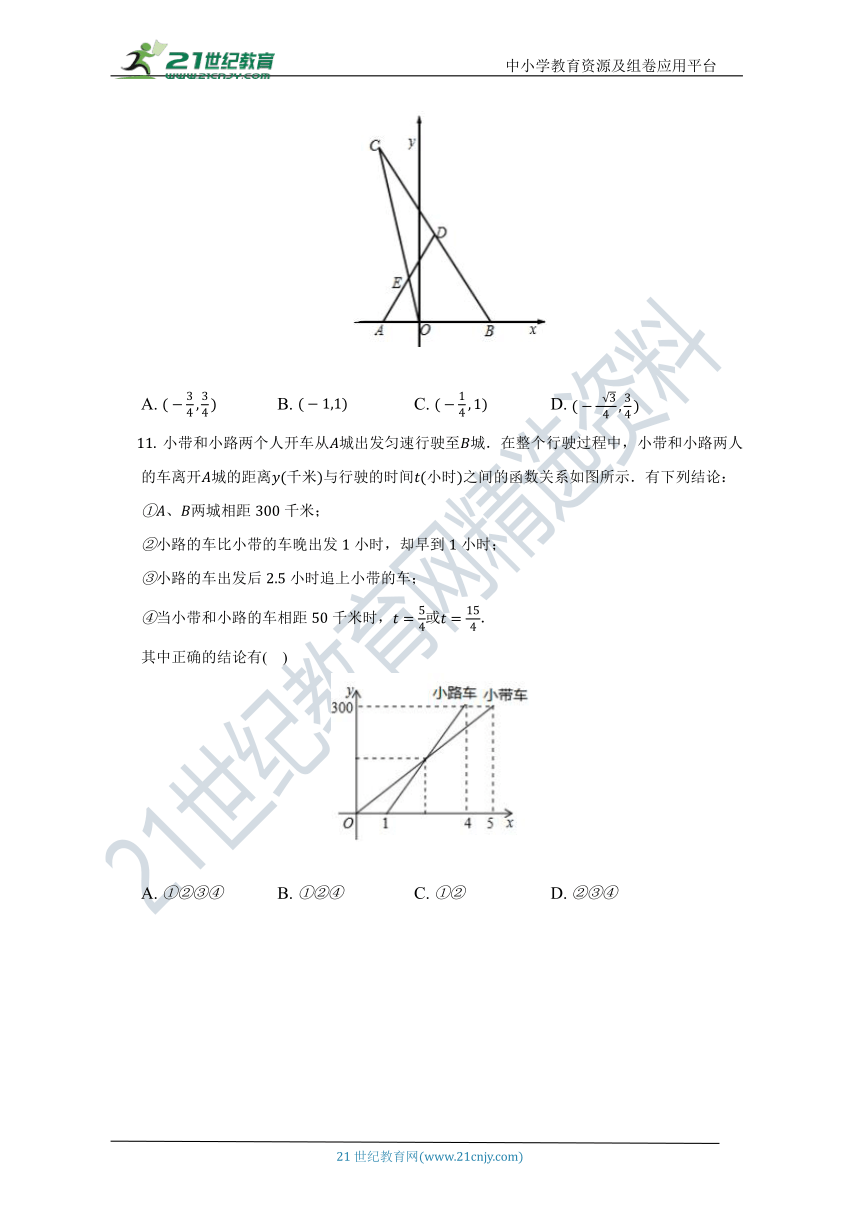
小带和小路两个人开车从城出发匀速行驶至城.在整个行驶过程中,小带和小路两人的车离开城的距离千米与行驶的时间小时之间的函数关系如图所示.有下列结论:
、两城相距千米;
小路的车比小带的车晚出发小时,却早到小时;
小路的车出发后小时追上小带的车;
当小带和小路的车相距千米时,或.
其中正确的结论有( )
A. B. C. D.
甲、乙两车从城出发匀速行驶至城.在整个行驶过程中,甲、乙两车离开城的距离千米与甲车行驶的时间小时之间的函数关系如图所示.则下列结论:
,两城相距千米;
乙车比甲车晚出发小时,却早到小时;
乙车出发后小时追上甲车;
当甲、乙两车相距千米时,或.
其中正确的结论有( )
A. 个 B. 个 C. 个 D. 个
第II卷(非选择题)
二、填空题(本大题共4小题,共12分)
甲、乙两人在同一平直的道路上同时、同起点、同方向出发,他们分别以不同的速度匀速跑步米甲的速度大于乙的速度,当甲第一次超出乙米时,甲停下来等候乙.甲、乙两人会合后,两人分别以原来的速度继续跑向终点,先到终点的人在终点休息.在整个跑步过程中,甲、乙两人之间的距离米与乙出发的时间秒之间的关系如图所示,则当甲到达终点时,乙跑了________米.
某工程队承建一条长为的乡村公路,预计工期为天,若每天修建公路的长度保持不变,则还未完成的公路长度与施工时间天之间的关系式为______.
已知是一次函数,则_________.
张师傅驾车从甲地到乙地匀速行驶,已知行驶中油箱剩余油量升与行驶时间小时之间的关系用如图的线段表示,根据这个图象求出与之间的函数关系式为,那么函数中,的系数表示的实际意义是________.
三、解答题(本大题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤)
本小题分
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发设慢车行驶的时间为,两车之间的距离为,图中的折线表示与之间的关系根据图象解答下列问题:
甲、乙两地之间的距离为
请解释图中点的实际意义
求慢车和快车的速度.
本小题分
快车与慢车分別从甲乙两地同时相向出发,匀速而行,快车到达乙地后停留,然后按原路原速返回,快车比慢车晚到达甲地,快慢两车距各自出发地的路程与所用的时的关系如图所示.
甲乙两地之间的路程为__________;快车的速度为______;慢车的速度为_______;
出发________,快慢两车距各自出发地的路程相等;
快慢两车出发___________相距.
本小题分
如图,在四边形中,,,为原点,点的坐标为,点的坐标为,点从点出发,以每秒个单位长度的速度沿向点运动,点同时从点出发,以每秒个单位长度的速度沿折线运动,当点达到点时,点也停止运动,从运动开始,设点运动的时间为秒.
当为何值时,四边形是矩形;
当为何值时,?
连接,记的面积为,求与的函数关系式.
本小题分
某旅游团在某天上午点从宾馆出发乘车到离宾馆的一个景点去游玩该汽车离开宾馆的距离与时间的关系可以用如图所示的折线图表示根据图像提供的信息解答下列问题:
求该团去这个景点时的平均速度.
该团在这个景点游玩了多长时间?
他们是几点几分返回的宾馆?
本小题分
新定义:对于关于的一次函数,我们称函数为一次函数的变函数其中为常数.
例如:对于关于的一次函数的变函数为.
关于的一次函数的变函数为,则当时, .
关于的一次函数的变函数为,关于的一次函数的变函数为,直接写出函数和函数的交点坐标.
关于的一次函数的变函数为,关于的一次函数的变函数为.
当时,函数的取值范围是 直接写出答案.
若函数和函数有且仅有两个交点,则的取值范围是 直接写出答案.
本小题分
一次函数的图象与轴交于点,与轴交于点,为坐标原点的面积为,且函数的值随的增大而增大.求:
点的坐标.
点的坐标及的值.
本小题分
如图,在平面直角坐标系中,直线与轴交于点,与轴交于点,以为腰在第二象限作等腰直角,.
求点的坐标.
是轴上的一个动点,是否存在这样的点,使得的值最大?如果不存在,请说明理由;如果存在,请求出点的坐标.
若以,,为顶点的三角形和全等点不与点重合,请直接写出点的坐标.
本小题分
某工厂安排名技工组装、、三个型号的玩具,按规定每天共组装件玩具,每名技工只组装同一型号的玩具,且至少有名技工组装同一个型号的玩具.
玩具型号 型 型 型
每名技工每天组装的数量个
每件玩具获得的利润元
设工厂安排名技工组装型玩具,名技工组装型玩具,根据上表提供的信息,求与之间的函数关系式,并求出的取值范围.
工厂如何安排生产任务,可以使得每天在这批玩具上获得的利润最大?请写出相应的生产分配方案并求出每天获得的最大利润值.
本小题分
某公司有型产品件,型产品件,分配给下属甲、乙两个商店销售,其中件给甲店,件给乙店,且都能卖完.两商店销售这两种产品每件的利润元如下表:
型利润 型利润
甲店
乙店
设分配给甲店型产品件,这家公司卖出这件产品的总利润为元,求关于的函数关系式,并求出的取值范围;
若要求总利润不低于元,有多少种不同分配方案,并将各种方案设计出来;
为了促销,公司决定仅对甲店型产品让利销售,每件让利元,但让利后型产品的每件利润仍高于甲店型产品的每件利润.甲店的型产品以及乙店的,型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
答案和解析
1.【答案】
【解析】
【分析】
本题考查了用图象表示变量之间的关系的有关知识,根据路程与时间的关系,可得甲乙的速度,根据相遇前甲行驶的路程除以乙行驶的速度,可得乙到达站需要的时间,根据相遇前乙行驶的路程除以甲行驶的速度,可得甲到达站需要的时间,再根据有理数的减法,可得答案.
【解答】
解:由纵坐标看出甲先行驶了千米,由横坐标看出甲行驶千米用了分钟,
甲的速度是千米分钟,
由纵坐标看出两地的距离是千米,
设乙的速度是千米分钟,由题意,得
,
解得千米分钟,
相遇后乙到达站还需分钟
相遇后甲到达站还需分钟,
当乙到达终点时,甲还需分钟到达终点,
故选D.
2.【答案】
【解析】
【分析】
根据题意可以判断哪个选项中的函数图象符合题意,从而可以解答本题.本题考查函数的图象,解答本题的关键是明确题意,利用数形结合的思想解答.
【解答】
解:由题意可得, 刚开始,小明跑步上山,随着的增加而减小,变化趋势比较快,
休息一段时间,这个过程,随着的增加不变, 慢慢走完剩下的路程,随着的增加而减小,变化趋势比较缓慢,
故选C.
3.【答案】
【解析】
【分析】
本题考查了函数图象,动点函数的图象的有关知识,读懂题意,把整个过程分解成分段图象是解题的关键.根据题意,把图象分为四段,第一段,小明从家出发去学校到妈妈发现小明的作业本落在家里,第二段妈妈骑车追赶到追上小明,第三段两人稍作停留,第四段妈妈骑车返回,小明继续步行前往学校,两人同时到达.分析图象,然后选择答案.
【解答】
解:根据题意可得,与的函数关系的大致图象分为四段,
第一段,小明从家出发去学校到妈妈发现小明的作业本落在家里,两人的距离在慢慢增大,
第二段,妈妈骑车追赶到追上小明,两人的距离在减小,
第三段,两人稍作停留,两人的距离为,
第四段,妈妈骑车返回,小明继续步行前往学校,两人同时到达,两人的距离在快速增大,
纵观各选项,只有选项的图象符合.
故选B.
4.【答案】
【解析】解:当点在上时,则,
则,为一次函数,
当时,;
当点在上时,
则,,
故,为一次函数,
当时,;
当点在上时,随的增大而减小,当时,,
故选:.
分点在上、点在上、点在上三种情况,求出函数表达式或确定随的变化情况即可求解.
本题考查的是四边形动点问题与一次函数结合,熟悉掌握四边形动点问题的解决办法和一次函数图象的相关性质,运用数形结合的思想是解题的关键.
5.【答案】
【解析】解:根据函数图象可以知:从到,随的增大而增大,经过了秒,运动了,因而,,故正确;
在段时,底边不变,高不变,因而面积不变,由图象可知,面积,故正确;
图中的点表示第秒时,表示点到达点,的面积是,故正确;
则个结论正确;
故选:.
根据题意得:动点在上运动的时间是秒,又由动点的速度,可得和的长;
由可得的长,又由,可以计算出的面积,计算可得的值;
根据图中的点表示第秒时,表示点到达点,即可得出的面积
本题考查了动点问题的函数图象:函数图象是典型的数形结合,图象应用信息广泛,通过看图获取信息,不仅可以解决生活中的实际问题,还可以提高分析问题、解决问题的能力.用图象解决问题时,要理清图象的含义即会识图.
6.【答案】
【解析】解:过点作于点,如图,
由题可知,当点从点运动到点,即从小变大时,也是先变小再变长,
而的面积不变,又,即是先变大再变小,
结合选项可知,选项是正确的;
故选:.
过点作于点,由题可知,当点从点运动到点,即从小变大时,也是先变小再变长,而的面积不变,又,即是先变大再变小,结合选项可得结论.
本题主要考查动点问题的函数图象,题中没有给任何的数据,需要通过变化趋势进行判断.
7.【答案】
【解析】
【分析】
本题主要考查了正比例函数的定义,正比例函数的定义条件是:为常数,,自变量次数为,
根据正比例函数的定义条件进行逐一分析即可.
【解答】
解:是正比例函数;
,整理得是正比例函数;
是常数,当时候,不是正比例函数;
,不是正比例函数,
所以有不是正比例函数,总共两个
故选:.
8.【答案】
【解析】
【分析】
本题考查一次函数的定义,解题的关键是正确理解一次函数的一般式,本题属于基础题型.形如,称为一次函数.
【解答】
解:,,,,
故选D
9.【答案】
【解析】
【分析】
本题考查了规律型中的点的坐标的变化,根据点的坐标的变化找出变化规律是解题的关键设坐标为,根据点,,,坐标的变化找出变化规律即可解答.
【解答】
解:设的坐标为,
,,,
,
,,,
的坐标为
故选A.
10.【答案】
【解析】
【分析】
本题考查一次函数的应用,待定系数法求函数的表达式,两点之间的距离公式,掌握一次函数的性质是解题的关键.
根据题意可求出点坐标含,易求直线和方程,联立可求点坐标,通过坐标使距离用参数表示,最终求出最短时点坐标.
【解答】
解:点是的中点,,,
,
当时,由,,
知,
直线方程为,
由于过原点,且,
,
直线方程为,
联立
即,
得
,
当时,最小,最小值为,
即;
当时,即,
直线方程为,
由于在轴上,
故时,,即,
此时,
故当时,最小,此时
故选A.
11.【答案】
【解析】
【分析】
本题主要考查一次函数的应用,掌握一次函数图象的意义是解题的关键,特别注意是小带车所用的时间.
观察图象可判断,由图象所给数据可求得小带、小路两车离开城的距离与时间的关系式,可求得两函数图象的交点,可判断,再令两函数解析式的差为,可求得,可判断,可得出答案.
【解答】
解:由图象可知、两城市之间的距离为,小带行驶的时间为小时,而小路是在小带出发小时后出发的,且用时小时,即比小带早到小时,
都正确;
设小带车离开城的距离与的关系式为,
把代入可求得,
,
设小路车离开城的距离与的关系式为,
把和代入可得,
解得:,
,
令,可得:,
解得:,
即小带车、小路车两直线的交点横坐标为,
此时小路车出发时间为小时,即小路车出发小时后追上小带车,
不正确;
令,可得,即,
当时,可解得,
当时,可解得,
又当时,,此时小路车还没出发,
当时,小路车到达城,;
综上可知当的值为或或或时,两车相距千米,
不正确;
故选C.
12.【答案】
【解析】
【分析】
本题主要考查一次函数的应用,掌握一次函数图象的意义是解题的关键,特别注意是甲车所用的时间.观察图象可判断,由图象所给数据可求得甲、乙两车离开城的距离与时间的关系式,可求得两函数图象的交点,可判断,再令两函数解析式的差为,可求得,可判断,可得出答案.
【解答】
解:由图象可知、两城市之间的距离为,甲行驶的时间为小时,而乙是在甲出发小时后出发的,且用时小时,即比甲早到小时,
都正确;
设甲车离开城的距离与的关系式为,
把代入可求得,
,
设乙车离开城的距离与的关系式为,
把和代入可得,解得
,
令可得:,解得,
即甲、乙两直线的交点横坐标为,
此时乙出发时间为小时,即乙车出发小时后追上甲车,
不正确;
令,可得,即,
当时,可解得,
当时,可解得,
又当时,,此时乙还没出发,
当时,乙到达城,;
综上可知当的值为或或或时,两车相距千米,
不正确;
综上可知正确的有共两个,
故选:.
13.【答案】
【解析】
【分析】
本题考查了用图象表示变量之间的关系,根据“速度路程时间”结合图象即可算出乙的速度,再根据“甲的速度乙的速度两者速度差”即可求出甲的速度,进而即可求出甲、乙会合地离起点的距离,结合总路程及二者的速度即可得出甲到终点时,乙离起点的距离,此题得解.
【解答】
解:由题意,知乙的速度为米秒.
甲的速度为米秒.
两人相距米时,甲跑的路程是米,此时离终点的距离为米.
从会合到终点,甲所用时间是秒,乙从会合点跑秒的路程是米.
当甲到达终点时,乙跑的总路程是米
故答案为.
14.【答案】
【解析】解:由题意,得
每天修,
,
故答案为:
根据总工程量减去已修的工程量,可得答案.
本题考查了函数关系式,利用总工程量减去已修的工程量是解题关键.
15.【答案】
【解析】
【分析】
此题主要考查了一次函数的定义,一次函数的定义条件是:、为常数,,自变量次数为根据一次函数定义可得,再解方程即可得到的值.
【解答】
解:由题意得:,
解得:,
故答案为.
16.【答案】表示每小时平均耗油升
【解析】
【分析】
本题主要考查的是一次函数的图象和应用的有关知识,又经过小时,汽车油箱剩余油量升,即每小时耗油升,进而解出此题的答案.
【解答】
解:函数中,的系数表示的实际意义是表示每小时平均耗油升.
故答案为表示每小时平均耗油升.
17.【答案】解:
图中点的实际意义:当行驶时,慢车和快车相遇.
由图象可知,慢车行驶的路程为,
所以慢车的速度为.
当慢车行驶时,慢车和快车相遇,两车行驶的路程之和为,
所以慢车和快车行驶的速度之和为,
所以快车的速度为.
【解析】见答案.
18.【答案】;;;
;
或或.
【解析】
【分析】
本题考查了用图像表示变量之间的关系,主要利用了时间、路程、速度三者之间的关系和追击问题的等量关系,难点在于表示出快车距离出发地的路程.
先得两地的距离,根据速度路程时间列式计算即可求出快车和慢车的速度;
根据两车的速度等条件可得出答案;
分别根据两车相遇前、两车相遇后以及快车从乙往甲返回途中,三种情况两车距离为时,列方程可解答.
【解答】
解:由图可知:甲乙两地之间的路程为;
快车的速度为:;
由题意得:快车小时到达甲地,则慢车小时到达甲地,
则慢车的速度为:;
故答案为:,,;
设经过小时后,快、慢两车距各自出发地的路程相等,
则
解得:,
答:出发小时,快、慢两车距各自出发地的路程相等;
故答案为:;
第一种情形第一次没有相遇前,相距,
则,
解得:,
第二种情形应是相遇后而快车没到乙地前,
解得:,
第三种情形是快车从乙往甲返回途中:,
解得:,
综上所述:快慢两车出发或或相距.
故答案为:或或.
19.【答案】解:点的坐标为,点的坐标为,
,,,
点运动的时间为秒,
,,
当时,四边形是矩形,
即,
解得,;
由题意得,
四边形为平行四边形时,,
即,
解得,;
四边形为等腰梯形时,若,则,
即,解得,;
当在上时,,,,
在中,,
即,化简得:,
,
原方程无实数根;
综上所述:当或时,.
如图,当点在上时,
,
则,
当点在上时,,,
则.
【解析】本题考查的是矩形的判定、平行四边形的判定和性质以及函数解析式的确定,掌握相关的性质定理和判定定理、灵活运用分情况讨论思想是解题的关键.
根据矩形的判定定理列出关系式,计算即可;
根据平行四边形的判定定理和性质、等腰梯形的性质以及勾股定理定理分情况解答;
分点在上和点在上两种情况,根据三角形的面积公式计算即可.
20.【答案】 解:千米时,
答:该团去景点时的平均速度是千米时;
由横坐标得出时到达景点,是离开景点,小时,
答:该团在旅游景点游玩了小时;
设返回途中函数关系式是,由题意,得
,
解得,
返回途中函数关系式是,
当时,,
返回到宾馆的时刻是点分.
【解析】本题考查了函数图象,观察函数图象得出路程与时间的关系是解题关键.
根据路程除以时间等于速度,可得答案;
根据路程不变,可得相应的自变量的范围;
根据待定系数法,可得函数关系式,根据自变量与函数值得对应关系,可得答案.
21.【答案】解:;
根据定义得:
::
求交点坐标:,解得;
解得:;
,无解;
,无解;
综上所述函数和函数的交点坐标为和;
;
.
【解析】
【分析】
本题考查一次函数的应用、两直线平行或相交等知识,解题的关键是理解题意,学会构建方程组确定两个函数的交点坐标,属于中考压轴题.
根据变函数的定义即可解决问题;
转化为方程组解决问题即可;
根据变函数的定义,求出特殊点的函数值即可解决问题;
利用方程组求出交点坐标即可解决问题;
【解答】
解:根据变函数定义,关于的一次函数的变函数为:
时,,
故答案为;
见答案;
由题意::
时,,时,,
时,,
故答案为;
由题意:::
易知两个函数的交点,,
观察图象可知:时,函数和函数有且仅有两个交点.
故答案为.
22.【答案】解:把代入得,
所以点坐标为;
为坐标原点的面积为,
,
,
函数的值随的增大而增大,
点的坐标为,
把点的坐标为代入得,
,
解得:.
【解析】本题考查了一次函数的性质,三角形的面积的有关知识.
根据轴上点的坐标特征,求自变量为时的函数值即可得到点坐标;
根据三角形面积公式得到,再利用一次函数的性质得点的坐标为,然后把点坐标代入即可计算出的值.
23.【答案】解:如图,过点作于点,
对于一次函数,
令,则
令,则,即,故,
,
,
,
,
,
,
是等腰直角三角形,
,
在和中,
,
,,
,
;
存在点,使得的值最大.
是轴上的一个动点,
,
当点在的延长线与轴的交点上时,,此时的值最大,
如图,延长交轴于点,设直线的解析式为,
,,
解得
直线的解析式为.
当时,,解得,
;
点的坐标为,,.
【解析】本题主要考查一次函数与等腰直角三角形的综合,用待定系数法确定函数的解析式,一次函数图象的性质,一次函数图象上点的坐标的特征,全等三角形的判定与性质等知识,利用点的坐标表示出相应线段的长度是解题的关键,注意分类讨论.
过点作于点,通过证明,求得线段,的长度即可得出结论;
延长,交轴于点,则此时的值最大,利用待定系数法求得直线的解析式,令即可求得点的横坐标;
分三种情况,分别过点作、轴的垂线,通过全等三角形的性质求出点到、轴的垂线段的长,即得点的坐标.
解:如图,,过点作轴于点,
过点作轴于点,过点作轴于点,
易证,
,,
由可知,,
,,
,,,
综上所述,点的坐标为,,,
故答案为:的坐标为,,.
24.【答案】解:设组装型、型、型玩具的技工分别为、、名.
根据题意得.
整理得,
,
组装型、型、型玩具的技工分别为、、名
由题意可知,解得,且是整数,
由题意可知:.
即是的一次函数
,
随的增大而减小
,且是整数
当时,的值最大.
此时元,即最大利润为元.
生产分配方案如下:组装型玩具人,型玩具人,型玩具人.
【解析】设组装型、型、型玩具的技工分别为、、人,然后根据玩具总个数为,列出等式,然后整理即可得到与的函数关系式,然后根据至少有名技工组装同一个型号的玩具列不等式组求解即可;
然后根据总利润三种类型玩具的利润和;每种玩具的利润玩具数量每个玩具的利润列出函数关系式,然后根据关系进行判断即可.
本题主要考查的是一次函数的应用,根据一次函数的性质判断出取得最大值是的取值是解题的关键.
25.【答案】解:由题意得,甲店型产品有件,乙店型有件,型有件,
则.
由,
解得;
由,
解得.
故,,,.
则有三种不同的分配方案.
时,甲店型件,型件,乙店型件,型件;
时,甲店型件,型件,乙店型件,型件;
时,甲店型件,型件,乙店型件,型件;
依题意:.
当时,,即甲店型件,型件,乙店型件,型件,能使总利润达到最大.
当时,,符合题意的各种方案,使总利润都一样.
当时,,即甲店型件,型件,乙店型件,型件,能使总利润达到最大.
【解析】根据所有产品数量及所给产品数量分别得到甲店型商品,乙店型商品,乙店型商品的数量,那么总利润等于每件相应商品的利润相应件数之和;根据各个店面的商品的数量为非负数可得自变量的取值范围;
让中的代数式,结合中自变量的取值可得相应的分配方案;
根据让利后型产品的每件利润仍高于甲店型产品的每件利润可得的取值,结合得到相应的总利润,根据的不同取值得到利润的函数应得到的最大值的方案即可.
此题主要考查了一次函数的应用;得到分配给甲乙两店的不同型号的产品的数量是解决本题的突破点;得到总利润的关系式是解决本题的关键;根据的不同取值得到相应的最大利润是解决本题的难点.
21世纪教育网(www.21cnjy.com)
浙教版初中数学八年级上册第五单元《一次函数》单元测试卷
考试范围:第五章;考试时间:120分钟;总分:120分
学校:___________姓名:___________班级:___________考号:___________
第I卷(选择题)
一、选择题(本大题共12小题,共36分。在每小题列出的选项中,选出符合题目的一项)
甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从地到地,乙驾车从地到地,他们分别以不同的速度匀速行驶.已知甲先出发分钟后,乙才出发,在整个过程中,甲、乙两人的距离千米与甲出发的时间分之间的关系如图所示,当乙到达终点时,甲还需分钟到达终点.( )
A. B. C. D.
明明在爬山的活动中,先快速跑步上山,累了停下来休息了一段时间后,再慢慢爬到山顶,下图中能大致反映明明离山顶的路程与登山时间的关系的是( )
A. B.
C. D.
早上,小明从家里步行去学校,出发一段时间后,小明妈妈发现小明的作业本落在家里,便带上作业本骑车追赶,途中追上小明两人稍作停留,妈妈骑车返回,小明继续步行前往学校,两人同时到达.设小明在途的时间为,两人之间的距离为,则下列选项中的图象能大致反映与之间关系的是( )
A. B.
C. D.
如图,在矩形中,,,是的中点,点在矩形的边上沿运动,则的面积与点经过的路程之间的函数关系式用图象表示大致是( )
A. B.
C. D.
如图,点是的中点,点在上,动点以每秒的速度沿图的边线运动,运动路径为:,相应的的面积关于运动时间的函数图象如图,若,有下列结论:
图中的长是;
图中的点表示第秒时,的值为;
图中的点表示第秒时,的值为.
其中,正确结论的个数是( )
A. B. C. D.
如图,已知在中,,点沿自向运动,作于,于,则的值与的长之间的函数图象大致是( )
A. B.
C. D.
下列函数其中是自变量中,不是正比例函数的个数有( )
;;是常数;.
A. 个 B. 个 C. 个 D. 个
下列函数关系式:;;;;其中表示一次函数的有( )
A. 个 B. 个 C. 个 D. 个
正方形,,,按如图所示放置,点,,,和点,,,,分别在直线和轴上,已知点,,,的坐标分别为,,,,则的坐标是( )
A. B. C. D.
如图,在平面直角坐标系中,,,,为线段的中点,线段交线段于点,当线段最短时,此时点的坐标为( )
A. B. C. D.
小带和小路两个人开车从城出发匀速行驶至城.在整个行驶过程中,小带和小路两人的车离开城的距离千米与行驶的时间小时之间的函数关系如图所示.有下列结论:
、两城相距千米;
小路的车比小带的车晚出发小时,却早到小时;
小路的车出发后小时追上小带的车;
当小带和小路的车相距千米时,或.
其中正确的结论有( )
A. B. C. D.
甲、乙两车从城出发匀速行驶至城.在整个行驶过程中,甲、乙两车离开城的距离千米与甲车行驶的时间小时之间的函数关系如图所示.则下列结论:
,两城相距千米;
乙车比甲车晚出发小时,却早到小时;
乙车出发后小时追上甲车;
当甲、乙两车相距千米时,或.
其中正确的结论有( )
A. 个 B. 个 C. 个 D. 个
第II卷(非选择题)
二、填空题(本大题共4小题,共12分)
甲、乙两人在同一平直的道路上同时、同起点、同方向出发,他们分别以不同的速度匀速跑步米甲的速度大于乙的速度,当甲第一次超出乙米时,甲停下来等候乙.甲、乙两人会合后,两人分别以原来的速度继续跑向终点,先到终点的人在终点休息.在整个跑步过程中,甲、乙两人之间的距离米与乙出发的时间秒之间的关系如图所示,则当甲到达终点时,乙跑了________米.
某工程队承建一条长为的乡村公路,预计工期为天,若每天修建公路的长度保持不变,则还未完成的公路长度与施工时间天之间的关系式为______.
已知是一次函数,则_________.
张师傅驾车从甲地到乙地匀速行驶,已知行驶中油箱剩余油量升与行驶时间小时之间的关系用如图的线段表示,根据这个图象求出与之间的函数关系式为,那么函数中,的系数表示的实际意义是________.
三、解答题(本大题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤)
本小题分
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发设慢车行驶的时间为,两车之间的距离为,图中的折线表示与之间的关系根据图象解答下列问题:
甲、乙两地之间的距离为
请解释图中点的实际意义
求慢车和快车的速度.
本小题分
快车与慢车分別从甲乙两地同时相向出发,匀速而行,快车到达乙地后停留,然后按原路原速返回,快车比慢车晚到达甲地,快慢两车距各自出发地的路程与所用的时的关系如图所示.
甲乙两地之间的路程为__________;快车的速度为______;慢车的速度为_______;
出发________,快慢两车距各自出发地的路程相等;
快慢两车出发___________相距.
本小题分
如图,在四边形中,,,为原点,点的坐标为,点的坐标为,点从点出发,以每秒个单位长度的速度沿向点运动,点同时从点出发,以每秒个单位长度的速度沿折线运动,当点达到点时,点也停止运动,从运动开始,设点运动的时间为秒.
当为何值时,四边形是矩形;
当为何值时,?
连接,记的面积为,求与的函数关系式.
本小题分
某旅游团在某天上午点从宾馆出发乘车到离宾馆的一个景点去游玩该汽车离开宾馆的距离与时间的关系可以用如图所示的折线图表示根据图像提供的信息解答下列问题:
求该团去这个景点时的平均速度.
该团在这个景点游玩了多长时间?
他们是几点几分返回的宾馆?
本小题分
新定义:对于关于的一次函数,我们称函数为一次函数的变函数其中为常数.
例如:对于关于的一次函数的变函数为.
关于的一次函数的变函数为,则当时, .
关于的一次函数的变函数为,关于的一次函数的变函数为,直接写出函数和函数的交点坐标.
关于的一次函数的变函数为,关于的一次函数的变函数为.
当时,函数的取值范围是 直接写出答案.
若函数和函数有且仅有两个交点,则的取值范围是 直接写出答案.
本小题分
一次函数的图象与轴交于点,与轴交于点,为坐标原点的面积为,且函数的值随的增大而增大.求:
点的坐标.
点的坐标及的值.
本小题分
如图,在平面直角坐标系中,直线与轴交于点,与轴交于点,以为腰在第二象限作等腰直角,.
求点的坐标.
是轴上的一个动点,是否存在这样的点,使得的值最大?如果不存在,请说明理由;如果存在,请求出点的坐标.
若以,,为顶点的三角形和全等点不与点重合,请直接写出点的坐标.
本小题分
某工厂安排名技工组装、、三个型号的玩具,按规定每天共组装件玩具,每名技工只组装同一型号的玩具,且至少有名技工组装同一个型号的玩具.
玩具型号 型 型 型
每名技工每天组装的数量个
每件玩具获得的利润元
设工厂安排名技工组装型玩具,名技工组装型玩具,根据上表提供的信息,求与之间的函数关系式,并求出的取值范围.
工厂如何安排生产任务,可以使得每天在这批玩具上获得的利润最大?请写出相应的生产分配方案并求出每天获得的最大利润值.
本小题分
某公司有型产品件,型产品件,分配给下属甲、乙两个商店销售,其中件给甲店,件给乙店,且都能卖完.两商店销售这两种产品每件的利润元如下表:
型利润 型利润
甲店
乙店
设分配给甲店型产品件,这家公司卖出这件产品的总利润为元,求关于的函数关系式,并求出的取值范围;
若要求总利润不低于元,有多少种不同分配方案,并将各种方案设计出来;
为了促销,公司决定仅对甲店型产品让利销售,每件让利元,但让利后型产品的每件利润仍高于甲店型产品的每件利润.甲店的型产品以及乙店的,型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
答案和解析
1.【答案】
【解析】
【分析】
本题考查了用图象表示变量之间的关系的有关知识,根据路程与时间的关系,可得甲乙的速度,根据相遇前甲行驶的路程除以乙行驶的速度,可得乙到达站需要的时间,根据相遇前乙行驶的路程除以甲行驶的速度,可得甲到达站需要的时间,再根据有理数的减法,可得答案.
【解答】
解:由纵坐标看出甲先行驶了千米,由横坐标看出甲行驶千米用了分钟,
甲的速度是千米分钟,
由纵坐标看出两地的距离是千米,
设乙的速度是千米分钟,由题意,得
,
解得千米分钟,
相遇后乙到达站还需分钟
相遇后甲到达站还需分钟,
当乙到达终点时,甲还需分钟到达终点,
故选D.
2.【答案】
【解析】
【分析】
根据题意可以判断哪个选项中的函数图象符合题意,从而可以解答本题.本题考查函数的图象,解答本题的关键是明确题意,利用数形结合的思想解答.
【解答】
解:由题意可得, 刚开始,小明跑步上山,随着的增加而减小,变化趋势比较快,
休息一段时间,这个过程,随着的增加不变, 慢慢走完剩下的路程,随着的增加而减小,变化趋势比较缓慢,
故选C.
3.【答案】
【解析】
【分析】
本题考查了函数图象,动点函数的图象的有关知识,读懂题意,把整个过程分解成分段图象是解题的关键.根据题意,把图象分为四段,第一段,小明从家出发去学校到妈妈发现小明的作业本落在家里,第二段妈妈骑车追赶到追上小明,第三段两人稍作停留,第四段妈妈骑车返回,小明继续步行前往学校,两人同时到达.分析图象,然后选择答案.
【解答】
解:根据题意可得,与的函数关系的大致图象分为四段,
第一段,小明从家出发去学校到妈妈发现小明的作业本落在家里,两人的距离在慢慢增大,
第二段,妈妈骑车追赶到追上小明,两人的距离在减小,
第三段,两人稍作停留,两人的距离为,
第四段,妈妈骑车返回,小明继续步行前往学校,两人同时到达,两人的距离在快速增大,
纵观各选项,只有选项的图象符合.
故选B.
4.【答案】
【解析】解:当点在上时,则,
则,为一次函数,
当时,;
当点在上时,
则,,
故,为一次函数,
当时,;
当点在上时,随的增大而减小,当时,,
故选:.
分点在上、点在上、点在上三种情况,求出函数表达式或确定随的变化情况即可求解.
本题考查的是四边形动点问题与一次函数结合,熟悉掌握四边形动点问题的解决办法和一次函数图象的相关性质,运用数形结合的思想是解题的关键.
5.【答案】
【解析】解:根据函数图象可以知:从到,随的增大而增大,经过了秒,运动了,因而,,故正确;
在段时,底边不变,高不变,因而面积不变,由图象可知,面积,故正确;
图中的点表示第秒时,表示点到达点,的面积是,故正确;
则个结论正确;
故选:.
根据题意得:动点在上运动的时间是秒,又由动点的速度,可得和的长;
由可得的长,又由,可以计算出的面积,计算可得的值;
根据图中的点表示第秒时,表示点到达点,即可得出的面积
本题考查了动点问题的函数图象:函数图象是典型的数形结合,图象应用信息广泛,通过看图获取信息,不仅可以解决生活中的实际问题,还可以提高分析问题、解决问题的能力.用图象解决问题时,要理清图象的含义即会识图.
6.【答案】
【解析】解:过点作于点,如图,
由题可知,当点从点运动到点,即从小变大时,也是先变小再变长,
而的面积不变,又,即是先变大再变小,
结合选项可知,选项是正确的;
故选:.
过点作于点,由题可知,当点从点运动到点,即从小变大时,也是先变小再变长,而的面积不变,又,即是先变大再变小,结合选项可得结论.
本题主要考查动点问题的函数图象,题中没有给任何的数据,需要通过变化趋势进行判断.
7.【答案】
【解析】
【分析】
本题主要考查了正比例函数的定义,正比例函数的定义条件是:为常数,,自变量次数为,
根据正比例函数的定义条件进行逐一分析即可.
【解答】
解:是正比例函数;
,整理得是正比例函数;
是常数,当时候,不是正比例函数;
,不是正比例函数,
所以有不是正比例函数,总共两个
故选:.
8.【答案】
【解析】
【分析】
本题考查一次函数的定义,解题的关键是正确理解一次函数的一般式,本题属于基础题型.形如,称为一次函数.
【解答】
解:,,,,
故选D
9.【答案】
【解析】
【分析】
本题考查了规律型中的点的坐标的变化,根据点的坐标的变化找出变化规律是解题的关键设坐标为,根据点,,,坐标的变化找出变化规律即可解答.
【解答】
解:设的坐标为,
,,,
,
,,,
的坐标为
故选A.
10.【答案】
【解析】
【分析】
本题考查一次函数的应用,待定系数法求函数的表达式,两点之间的距离公式,掌握一次函数的性质是解题的关键.
根据题意可求出点坐标含,易求直线和方程,联立可求点坐标,通过坐标使距离用参数表示,最终求出最短时点坐标.
【解答】
解:点是的中点,,,
,
当时,由,,
知,
直线方程为,
由于过原点,且,
,
直线方程为,
联立
即,
得
,
当时,最小,最小值为,
即;
当时,即,
直线方程为,
由于在轴上,
故时,,即,
此时,
故当时,最小,此时
故选A.
11.【答案】
【解析】
【分析】
本题主要考查一次函数的应用,掌握一次函数图象的意义是解题的关键,特别注意是小带车所用的时间.
观察图象可判断,由图象所给数据可求得小带、小路两车离开城的距离与时间的关系式,可求得两函数图象的交点,可判断,再令两函数解析式的差为,可求得,可判断,可得出答案.
【解答】
解:由图象可知、两城市之间的距离为,小带行驶的时间为小时,而小路是在小带出发小时后出发的,且用时小时,即比小带早到小时,
都正确;
设小带车离开城的距离与的关系式为,
把代入可求得,
,
设小路车离开城的距离与的关系式为,
把和代入可得,
解得:,
,
令,可得:,
解得:,
即小带车、小路车两直线的交点横坐标为,
此时小路车出发时间为小时,即小路车出发小时后追上小带车,
不正确;
令,可得,即,
当时,可解得,
当时,可解得,
又当时,,此时小路车还没出发,
当时,小路车到达城,;
综上可知当的值为或或或时,两车相距千米,
不正确;
故选C.
12.【答案】
【解析】
【分析】
本题主要考查一次函数的应用,掌握一次函数图象的意义是解题的关键,特别注意是甲车所用的时间.观察图象可判断,由图象所给数据可求得甲、乙两车离开城的距离与时间的关系式,可求得两函数图象的交点,可判断,再令两函数解析式的差为,可求得,可判断,可得出答案.
【解答】
解:由图象可知、两城市之间的距离为,甲行驶的时间为小时,而乙是在甲出发小时后出发的,且用时小时,即比甲早到小时,
都正确;
设甲车离开城的距离与的关系式为,
把代入可求得,
,
设乙车离开城的距离与的关系式为,
把和代入可得,解得
,
令可得:,解得,
即甲、乙两直线的交点横坐标为,
此时乙出发时间为小时,即乙车出发小时后追上甲车,
不正确;
令,可得,即,
当时,可解得,
当时,可解得,
又当时,,此时乙还没出发,
当时,乙到达城,;
综上可知当的值为或或或时,两车相距千米,
不正确;
综上可知正确的有共两个,
故选:.
13.【答案】
【解析】
【分析】
本题考查了用图象表示变量之间的关系,根据“速度路程时间”结合图象即可算出乙的速度,再根据“甲的速度乙的速度两者速度差”即可求出甲的速度,进而即可求出甲、乙会合地离起点的距离,结合总路程及二者的速度即可得出甲到终点时,乙离起点的距离,此题得解.
【解答】
解:由题意,知乙的速度为米秒.
甲的速度为米秒.
两人相距米时,甲跑的路程是米,此时离终点的距离为米.
从会合到终点,甲所用时间是秒,乙从会合点跑秒的路程是米.
当甲到达终点时,乙跑的总路程是米
故答案为.
14.【答案】
【解析】解:由题意,得
每天修,
,
故答案为:
根据总工程量减去已修的工程量,可得答案.
本题考查了函数关系式,利用总工程量减去已修的工程量是解题关键.
15.【答案】
【解析】
【分析】
此题主要考查了一次函数的定义,一次函数的定义条件是:、为常数,,自变量次数为根据一次函数定义可得,再解方程即可得到的值.
【解答】
解:由题意得:,
解得:,
故答案为.
16.【答案】表示每小时平均耗油升
【解析】
【分析】
本题主要考查的是一次函数的图象和应用的有关知识,又经过小时,汽车油箱剩余油量升,即每小时耗油升,进而解出此题的答案.
【解答】
解:函数中,的系数表示的实际意义是表示每小时平均耗油升.
故答案为表示每小时平均耗油升.
17.【答案】解:
图中点的实际意义:当行驶时,慢车和快车相遇.
由图象可知,慢车行驶的路程为,
所以慢车的速度为.
当慢车行驶时,慢车和快车相遇,两车行驶的路程之和为,
所以慢车和快车行驶的速度之和为,
所以快车的速度为.
【解析】见答案.
18.【答案】;;;
;
或或.
【解析】
【分析】
本题考查了用图像表示变量之间的关系,主要利用了时间、路程、速度三者之间的关系和追击问题的等量关系,难点在于表示出快车距离出发地的路程.
先得两地的距离,根据速度路程时间列式计算即可求出快车和慢车的速度;
根据两车的速度等条件可得出答案;
分别根据两车相遇前、两车相遇后以及快车从乙往甲返回途中,三种情况两车距离为时,列方程可解答.
【解答】
解:由图可知:甲乙两地之间的路程为;
快车的速度为:;
由题意得:快车小时到达甲地,则慢车小时到达甲地,
则慢车的速度为:;
故答案为:,,;
设经过小时后,快、慢两车距各自出发地的路程相等,
则
解得:,
答:出发小时,快、慢两车距各自出发地的路程相等;
故答案为:;
第一种情形第一次没有相遇前,相距,
则,
解得:,
第二种情形应是相遇后而快车没到乙地前,
解得:,
第三种情形是快车从乙往甲返回途中:,
解得:,
综上所述:快慢两车出发或或相距.
故答案为:或或.
19.【答案】解:点的坐标为,点的坐标为,
,,,
点运动的时间为秒,
,,
当时,四边形是矩形,
即,
解得,;
由题意得,
四边形为平行四边形时,,
即,
解得,;
四边形为等腰梯形时,若,则,
即,解得,;
当在上时,,,,
在中,,
即,化简得:,
,
原方程无实数根;
综上所述:当或时,.
如图,当点在上时,
,
则,
当点在上时,,,
则.
【解析】本题考查的是矩形的判定、平行四边形的判定和性质以及函数解析式的确定,掌握相关的性质定理和判定定理、灵活运用分情况讨论思想是解题的关键.
根据矩形的判定定理列出关系式,计算即可;
根据平行四边形的判定定理和性质、等腰梯形的性质以及勾股定理定理分情况解答;
分点在上和点在上两种情况,根据三角形的面积公式计算即可.
20.【答案】 解:千米时,
答:该团去景点时的平均速度是千米时;
由横坐标得出时到达景点,是离开景点,小时,
答:该团在旅游景点游玩了小时;
设返回途中函数关系式是,由题意,得
,
解得,
返回途中函数关系式是,
当时,,
返回到宾馆的时刻是点分.
【解析】本题考查了函数图象,观察函数图象得出路程与时间的关系是解题关键.
根据路程除以时间等于速度,可得答案;
根据路程不变,可得相应的自变量的范围;
根据待定系数法,可得函数关系式,根据自变量与函数值得对应关系,可得答案.
21.【答案】解:;
根据定义得:
::
求交点坐标:,解得;
解得:;
,无解;
,无解;
综上所述函数和函数的交点坐标为和;
;
.
【解析】
【分析】
本题考查一次函数的应用、两直线平行或相交等知识,解题的关键是理解题意,学会构建方程组确定两个函数的交点坐标,属于中考压轴题.
根据变函数的定义即可解决问题;
转化为方程组解决问题即可;
根据变函数的定义,求出特殊点的函数值即可解决问题;
利用方程组求出交点坐标即可解决问题;
【解答】
解:根据变函数定义,关于的一次函数的变函数为:
时,,
故答案为;
见答案;
由题意::
时,,时,,
时,,
故答案为;
由题意:::
易知两个函数的交点,,
观察图象可知:时,函数和函数有且仅有两个交点.
故答案为.
22.【答案】解:把代入得,
所以点坐标为;
为坐标原点的面积为,
,
,
函数的值随的增大而增大,
点的坐标为,
把点的坐标为代入得,
,
解得:.
【解析】本题考查了一次函数的性质,三角形的面积的有关知识.
根据轴上点的坐标特征,求自变量为时的函数值即可得到点坐标;
根据三角形面积公式得到,再利用一次函数的性质得点的坐标为,然后把点坐标代入即可计算出的值.
23.【答案】解:如图,过点作于点,
对于一次函数,
令,则
令,则,即,故,
,
,
,
,
,
,
是等腰直角三角形,
,
在和中,
,
,,
,
;
存在点,使得的值最大.
是轴上的一个动点,
,
当点在的延长线与轴的交点上时,,此时的值最大,
如图,延长交轴于点,设直线的解析式为,
,,
解得
直线的解析式为.
当时,,解得,
;
点的坐标为,,.
【解析】本题主要考查一次函数与等腰直角三角形的综合,用待定系数法确定函数的解析式,一次函数图象的性质,一次函数图象上点的坐标的特征,全等三角形的判定与性质等知识,利用点的坐标表示出相应线段的长度是解题的关键,注意分类讨论.
过点作于点,通过证明,求得线段,的长度即可得出结论;
延长,交轴于点,则此时的值最大,利用待定系数法求得直线的解析式,令即可求得点的横坐标;
分三种情况,分别过点作、轴的垂线,通过全等三角形的性质求出点到、轴的垂线段的长,即得点的坐标.
解:如图,,过点作轴于点,
过点作轴于点,过点作轴于点,
易证,
,,
由可知,,
,,
,,,
综上所述,点的坐标为,,,
故答案为:的坐标为,,.
24.【答案】解:设组装型、型、型玩具的技工分别为、、名.
根据题意得.
整理得,
,
组装型、型、型玩具的技工分别为、、名
由题意可知,解得,且是整数,
由题意可知:.
即是的一次函数
,
随的增大而减小
,且是整数
当时,的值最大.
此时元,即最大利润为元.
生产分配方案如下:组装型玩具人,型玩具人,型玩具人.
【解析】设组装型、型、型玩具的技工分别为、、人,然后根据玩具总个数为,列出等式,然后整理即可得到与的函数关系式,然后根据至少有名技工组装同一个型号的玩具列不等式组求解即可;
然后根据总利润三种类型玩具的利润和;每种玩具的利润玩具数量每个玩具的利润列出函数关系式,然后根据关系进行判断即可.
本题主要考查的是一次函数的应用,根据一次函数的性质判断出取得最大值是的取值是解题的关键.
25.【答案】解:由题意得,甲店型产品有件,乙店型有件,型有件,
则.
由,
解得;
由,
解得.
故,,,.
则有三种不同的分配方案.
时,甲店型件,型件,乙店型件,型件;
时,甲店型件,型件,乙店型件,型件;
时,甲店型件,型件,乙店型件,型件;
依题意:.
当时,,即甲店型件,型件,乙店型件,型件,能使总利润达到最大.
当时,,符合题意的各种方案,使总利润都一样.
当时,,即甲店型件,型件,乙店型件,型件,能使总利润达到最大.
【解析】根据所有产品数量及所给产品数量分别得到甲店型商品,乙店型商品,乙店型商品的数量,那么总利润等于每件相应商品的利润相应件数之和;根据各个店面的商品的数量为非负数可得自变量的取值范围;
让中的代数式,结合中自变量的取值可得相应的分配方案;
根据让利后型产品的每件利润仍高于甲店型产品的每件利润可得的取值,结合得到相应的总利润,根据的不同取值得到利润的函数应得到的最大值的方案即可.
此题主要考查了一次函数的应用;得到分配给甲乙两店的不同型号的产品的数量是解决本题的突破点;得到总利润的关系式是解决本题的关键;根据的不同取值得到相应的最大利润是解决本题的难点.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
