1.1锐角三角函数 课件 (23张ppt)
文档属性
| 名称 | 1.1锐角三角函数 课件 (23张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-15 00:00:00 | ||
图片预览



文档简介
(共23张PPT)
1.1 锐角三角函数
浙教版 九年级下册
学习目标
经历锐角的正弦、余弦和正切的探索过程,了解三角函数的概念.
掌握正弦、余弦和正切的符号,会用符号表示一个锐角的三角函数.(重点)
会根据锐角三角函数的定义求锐角三角函数值.(难点)
A
P
Q
B'
C'
合作学习 感悟新知
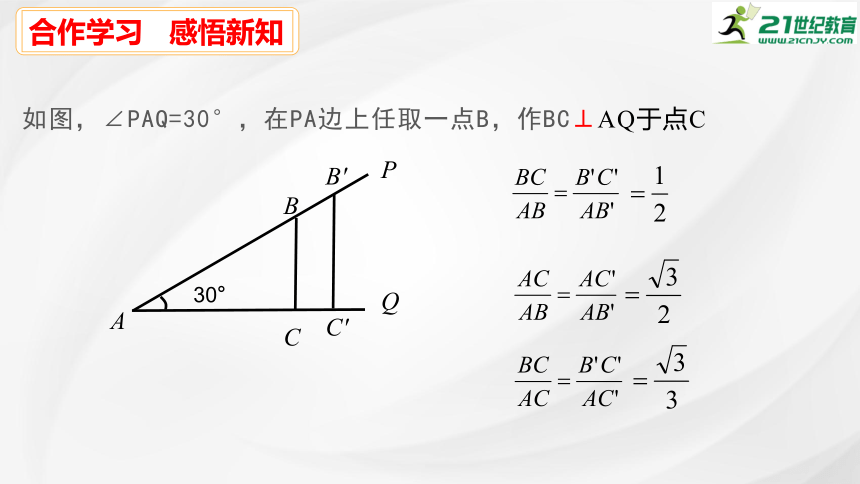
如图,∠PAQ=30°,在PA边上任取一点B,作BC⊥AQ于点C
30°
B
C
A
B
C
B'
C'
合作学习 感悟新知
45°
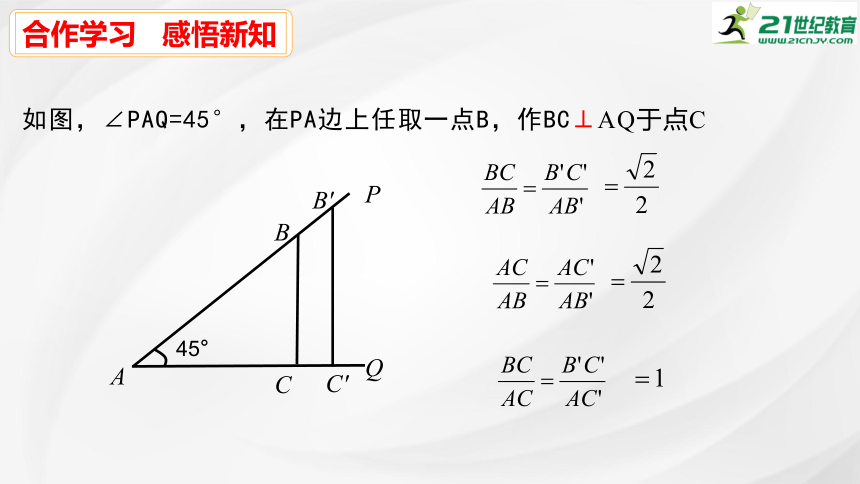
如图,∠PAQ=45°,在PA边上任取一点B,作BC⊥AQ于点C
P
Q
A
B
C
B'
C'
合作学习 感悟新知
60°
P
Q
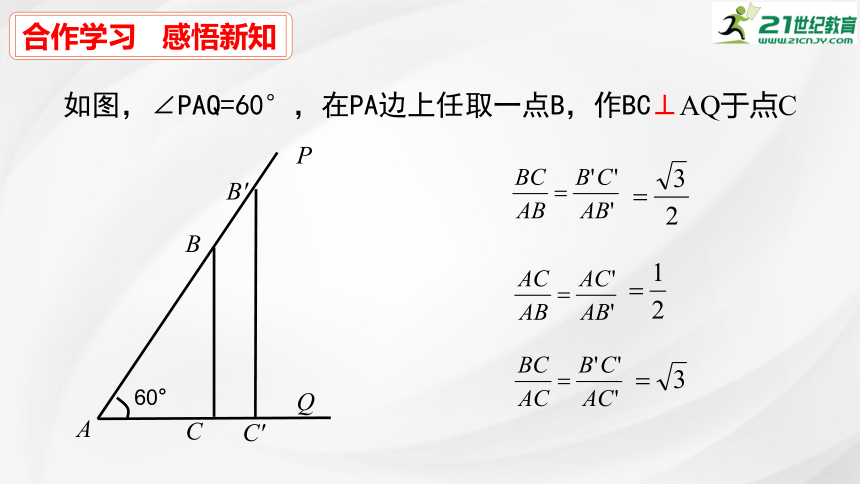
如图,∠PAQ=60°,在PA边上任取一点B,作BC⊥AQ于点C
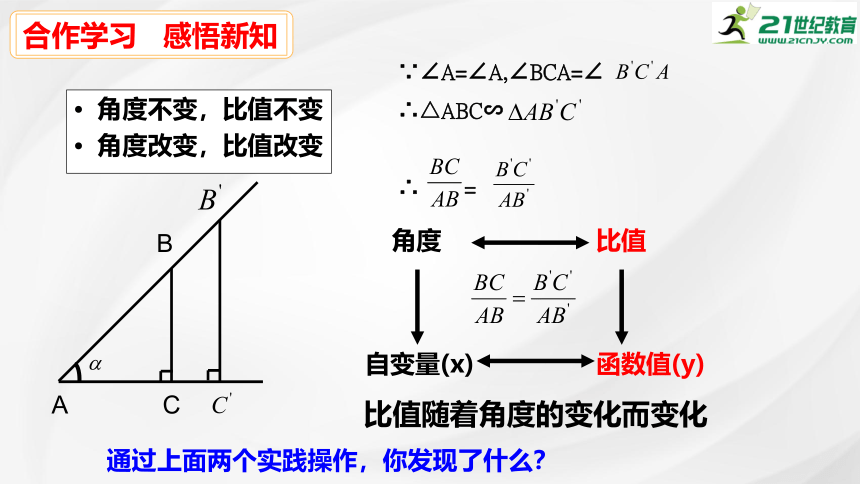
角度不变,比值不变
角度改变,比值改变
角度
比值
比值随着角度的变化而变化
∵∠A=∠A,∠BCA=∠
∴△ABC∽
∴ =
A
C
B
函数值(y)
自变量(x)
合作学习 感悟新知
通过上面两个实践操作,你发现了什么?
对于锐角A的每一个确定的值,其对边与斜边、邻边与斜边、对边与邻边的比值也是唯一确定的。
结论
比较发现“角度改变,比值改变”。.
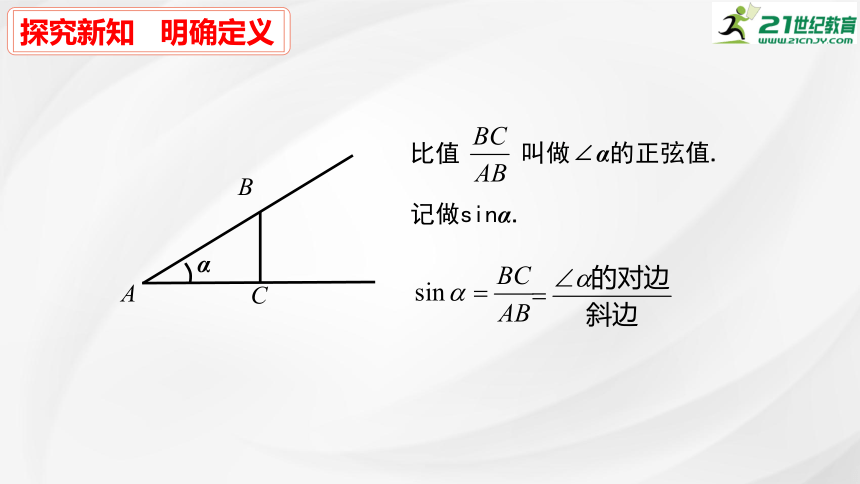
探究新知 明确定义
A
B
C
α
比值
叫做∠α的正弦值.
记做sinα.
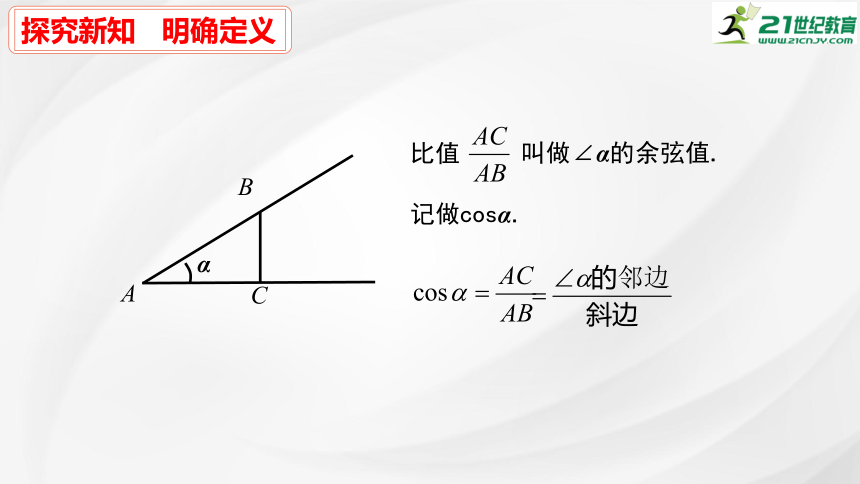
探究新知 明确定义
A
B
C
α
比值
叫做∠α的余弦值.
记做cosα.
探究新知 明确定义
A
B
C
α
比值
叫做∠α的正切值.
记做tanα.
正弦: sin A= ,如图,sin A=______.
余弦: cos A= ,如图,cos A=________.
正切: tan A= ,如图,tan A=________.
探究新知 明确定义
我们可以发现,锐角三角函数的值都是正实数,那么你知道sinA 和cosA 的取值范围吗?
0<cosA<1
0<sinA<1
tanA>0
A
B
C
如图,在Rt△ABC中,∠C=90°,AB=5,BC=3,求∠A、∠B的正弦、余弦和正切.
5
3
4
例题学习 巩固概念
观察以上计算结果,你发现了什么
解: 在Rt△ABC中
∵
∴
∴
由于∠A+∠B=90°
A
B
C
变式1.如图,在Rt△ABC中,∠C=90°,AC=5,BC=3,求∠B的正弦、余弦和正切.
3
5
变式练习 巩固概念
A
B
C
变式2.如图,在Rt△ABC中,∠C=90°,AC:BC=5:4,求∠B的正弦、余弦和正切.
4x
5x
变式练习 巩固概念
A
B
C
变式3.如图,在Rt△ABC中,∠C=90°, ,
求∠B的正弦、余弦和正切.
变式练习 巩固概念
5x
3x
4x
A
B
C
变式4.如图,在Rt△ABC中,∠C=90°, ,
求∠BCD的正弦、余弦和正切.
变式练习 巩固概念
5x
3x
4x
CD⊥AB,
D
课堂练习
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点
D,BC=3,AC=4,求sin∠DCB的值.
解:在Rt△ABC中,
∵CD⊥AB, ∴∠DCB+∠B=90°,
∵∠A+∠B=90°, ∴∠A=∠DCB,
做一做
做一做
如图, ∠C=90°,CD⊥AB.
在上图中,若BD=6,CD=12.求cos A的值.
┍
┌
A
C
B
D
课堂练习
1、如图,将△ABC放在每个小正方形的边长为1的网格中,点A,B,C均在格点上,则tanA的值是( )
A、 B、 C、 2 D、
D
做一做
4.905m
回归情景 巩固新知
课堂总结
同角三角函数间的关系:
sin 2A+cos 2A= __1__(0°<∠A<90°).
∠A+∠B=90°
4.求锐角三角函数时,勾股定理的运用是很重要的.
求锐角的三角函数值的三种方法:
1.在直角三角形里,确定各个边,根据定义直接求出.
2.利用相似、全等等关系,寻找与所求角相等的角
(若该角的三角函数值知道或者易求).
3.利用互余的两个角间的特殊关系求.
归纳小结 反思提高
https://www.21cnjy.com/help/help_extract.php
1.1 锐角三角函数
浙教版 九年级下册
学习目标
经历锐角的正弦、余弦和正切的探索过程,了解三角函数的概念.
掌握正弦、余弦和正切的符号,会用符号表示一个锐角的三角函数.(重点)
会根据锐角三角函数的定义求锐角三角函数值.(难点)
A
P
Q
B'
C'
合作学习 感悟新知
如图,∠PAQ=30°,在PA边上任取一点B,作BC⊥AQ于点C
30°
B
C
A
B
C
B'
C'
合作学习 感悟新知
45°
如图,∠PAQ=45°,在PA边上任取一点B,作BC⊥AQ于点C
P
Q
A
B
C
B'
C'
合作学习 感悟新知
60°
P
Q
如图,∠PAQ=60°,在PA边上任取一点B,作BC⊥AQ于点C
角度不变,比值不变
角度改变,比值改变
角度
比值
比值随着角度的变化而变化
∵∠A=∠A,∠BCA=∠
∴△ABC∽
∴ =
A
C
B
函数值(y)
自变量(x)
合作学习 感悟新知
通过上面两个实践操作,你发现了什么?
对于锐角A的每一个确定的值,其对边与斜边、邻边与斜边、对边与邻边的比值也是唯一确定的。
结论
比较发现“角度改变,比值改变”。.
探究新知 明确定义
A
B
C
α
比值
叫做∠α的正弦值.
记做sinα.
探究新知 明确定义
A
B
C
α
比值
叫做∠α的余弦值.
记做cosα.
探究新知 明确定义
A
B
C
α
比值
叫做∠α的正切值.
记做tanα.
正弦: sin A= ,如图,sin A=______.
余弦: cos A= ,如图,cos A=________.
正切: tan A= ,如图,tan A=________.
探究新知 明确定义
我们可以发现,锐角三角函数的值都是正实数,那么你知道sinA 和cosA 的取值范围吗?
0<cosA<1
0<sinA<1
tanA>0
A
B
C
如图,在Rt△ABC中,∠C=90°,AB=5,BC=3,求∠A、∠B的正弦、余弦和正切.
5
3
4
例题学习 巩固概念
观察以上计算结果,你发现了什么
解: 在Rt△ABC中
∵
∴
∴
由于∠A+∠B=90°
A
B
C
变式1.如图,在Rt△ABC中,∠C=90°,AC=5,BC=3,求∠B的正弦、余弦和正切.
3
5
变式练习 巩固概念
A
B
C
变式2.如图,在Rt△ABC中,∠C=90°,AC:BC=5:4,求∠B的正弦、余弦和正切.
4x
5x
变式练习 巩固概念
A
B
C
变式3.如图,在Rt△ABC中,∠C=90°, ,
求∠B的正弦、余弦和正切.
变式练习 巩固概念
5x
3x
4x
A
B
C
变式4.如图,在Rt△ABC中,∠C=90°, ,
求∠BCD的正弦、余弦和正切.
变式练习 巩固概念
5x
3x
4x
CD⊥AB,
D
课堂练习
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点
D,BC=3,AC=4,求sin∠DCB的值.
解:在Rt△ABC中,
∵CD⊥AB, ∴∠DCB+∠B=90°,
∵∠A+∠B=90°, ∴∠A=∠DCB,
做一做
做一做
如图, ∠C=90°,CD⊥AB.
在上图中,若BD=6,CD=12.求cos A的值.
┍
┌
A
C
B
D
课堂练习
1、如图,将△ABC放在每个小正方形的边长为1的网格中,点A,B,C均在格点上,则tanA的值是( )
A、 B、 C、 2 D、
D
做一做
4.905m
回归情景 巩固新知
课堂总结
同角三角函数间的关系:
sin 2A+cos 2A= __1__(0°<∠A<90°).
∠A+∠B=90°
4.求锐角三角函数时,勾股定理的运用是很重要的.
求锐角的三角函数值的三种方法:
1.在直角三角形里,确定各个边,根据定义直接求出.
2.利用相似、全等等关系,寻找与所求角相等的角
(若该角的三角函数值知道或者易求).
3.利用互余的两个角间的特殊关系求.
归纳小结 反思提高
https://www.21cnjy.com/help/help_extract.php
