第3章 圆中的分类讨论 课件(共15张PPT)
文档属性
| 名称 | 第3章 圆中的分类讨论 课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 664.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-15 21:00:31 | ||
图片预览

文档简介
(共15张PPT)
圆中的分类讨论
浙教版数学九年级(上)专题复习
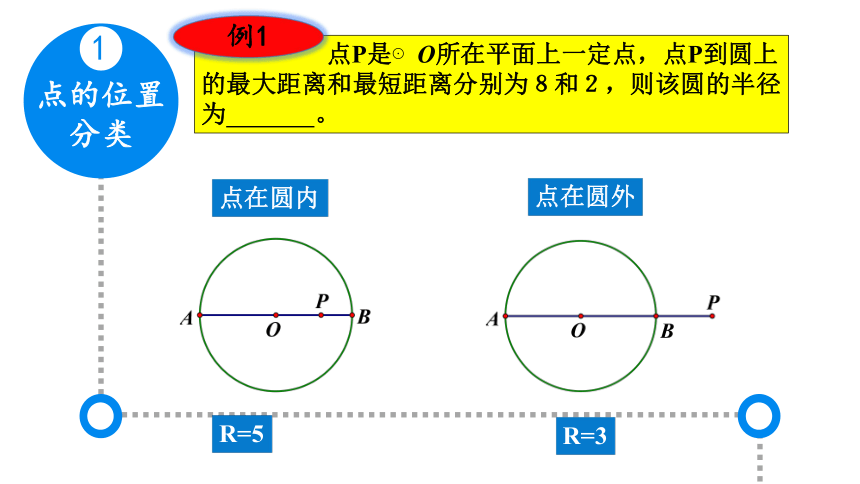
点的位置分类
1
点P是⊙O所在平面上一定点,点P到圆上的最大距离和最短距离分别为8和2,则该圆的半径为 。
例1
点在圆内
点在圆外
R=5
R=3
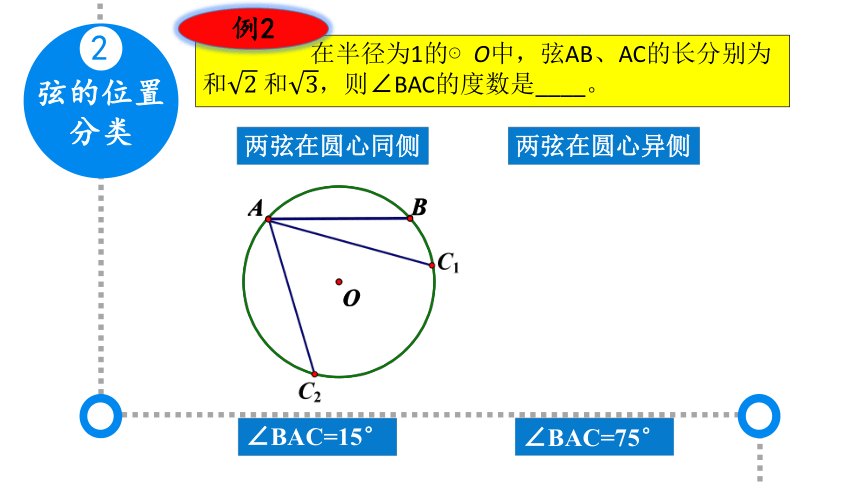
弦的位置
分类
2
在半径为1的⊙O中,弦AB、AC的长分别为 和 和,则∠BAC的度数是____。
例2
两弦在圆心同侧
两弦在圆心异侧
∠BAC=15°
∠BAC=75°
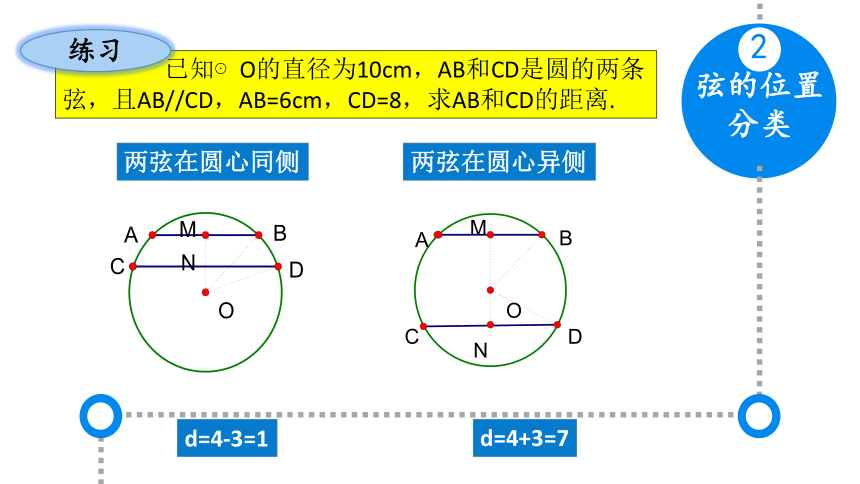
弦的位置分类
2
已知⊙O的直径为10cm,AB和CD是圆的两条弦,且AB//CD,AB=6cm,CD=8,求AB和CD的距离.
练习
两弦在圆心同侧
两弦在圆心异侧
d=4-3=1
d=4+3=7
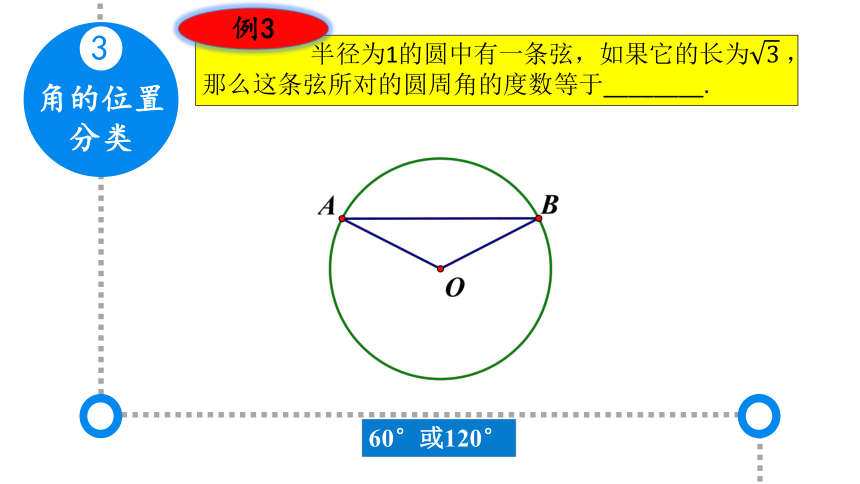
角的位置
分类
3
半径为1的圆中有一条弦,如果它的长为 ,那么这条弦所对的圆周角的度数等于________.
例3
60°或120°
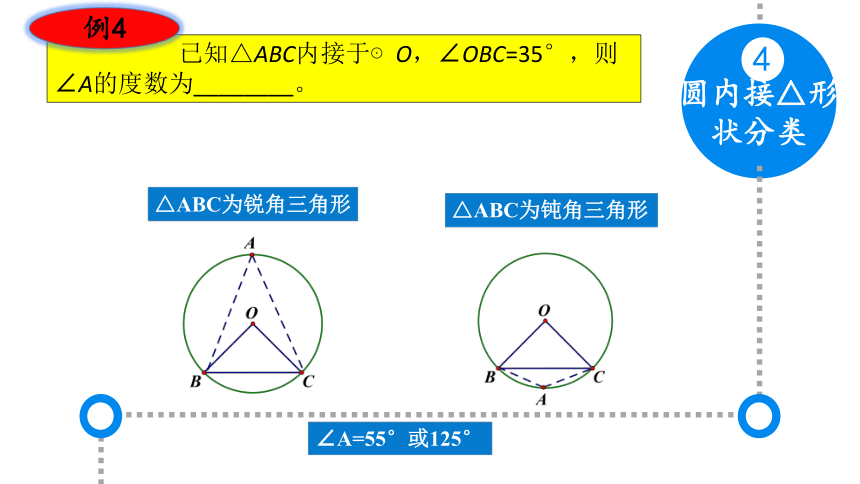
圆内接△形状分类
4
已知△ABC内接于⊙O,∠OBC=35°,则∠A的度数为________。
例4
△ABC为锐角三角形
△ABC为钝角三角形
∠A=55°或125°
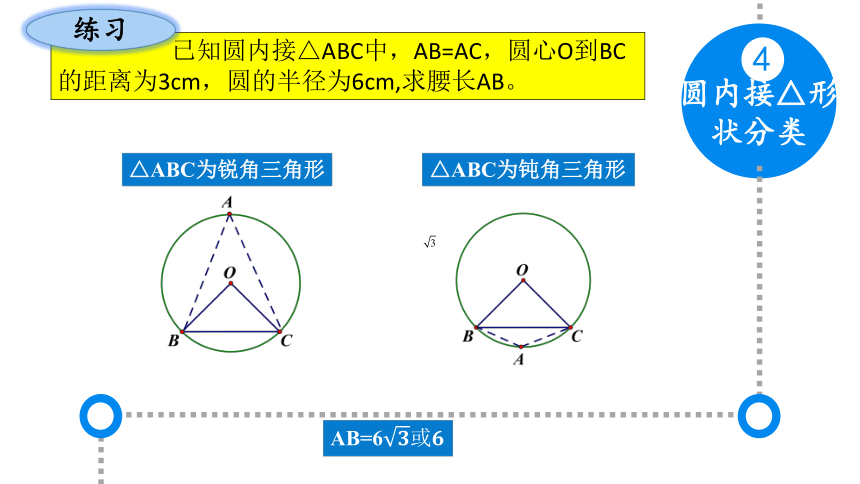
圆内接△形状分类
4
△ABC为锐角三角形
已知圆内接△ABC中,AB=AC,圆心O到BC的距离为3cm,圆的半径为6cm,求腰长AB。
练习
△ABC为钝角三角形
AB=6
巩固
练习题
5
已知横截面直径为100cm的圆形下水道,如果水面宽AB为80cm,求下水道中水的最大深度.
如图,AB是圆O的弦,AC是圆O的切线,∠BAC=60° ,则弦AB所对的圆周角等于__________.
已知在直径AB为26的半圆上有一点C,CD⊥AB,垂足为D,且CD=12,求AD的长.
2
1
3
答案
已知横截面直径为100cm的圆形下水道,如果水面宽AB为80cm,求下水道中水的最大深度.
1
20cm或80cm
答案
如图3,AB是圆O的弦,AC是圆O的切线, ∠BAC=60° ,则弦AB所对的圆周角等于__________.
2
60°或120°
答案
已知在直径AB为26的半圆上有一点C,CD⊥AB,垂足为D,且CD=12,求AD的长.
3
8或18
主要内容
12
01
02
03
04
05
点的位置
分类
弦的位置
分类
圆内接△形
状分类
圆周角的位置分类
巩固练习题
答案
已知在直径AB为50的半圆上有一点C,CD⊥AB,垂足为D,且CD=24,求AD的长.
练习
18或32
答案
已知横截面直径为130cm的圆形下水道,如果水面宽AB为120cm,求下水道中水的最大深度.
25cm或90cm
练习
感谢您的聆听!
圆中的分类讨论
浙教版数学九年级(上)专题复习
点的位置分类
1
点P是⊙O所在平面上一定点,点P到圆上的最大距离和最短距离分别为8和2,则该圆的半径为 。
例1
点在圆内
点在圆外
R=5
R=3
弦的位置
分类
2
在半径为1的⊙O中,弦AB、AC的长分别为 和 和,则∠BAC的度数是____。
例2
两弦在圆心同侧
两弦在圆心异侧
∠BAC=15°
∠BAC=75°
弦的位置分类
2
已知⊙O的直径为10cm,AB和CD是圆的两条弦,且AB//CD,AB=6cm,CD=8,求AB和CD的距离.
练习
两弦在圆心同侧
两弦在圆心异侧
d=4-3=1
d=4+3=7
角的位置
分类
3
半径为1的圆中有一条弦,如果它的长为 ,那么这条弦所对的圆周角的度数等于________.
例3
60°或120°
圆内接△形状分类
4
已知△ABC内接于⊙O,∠OBC=35°,则∠A的度数为________。
例4
△ABC为锐角三角形
△ABC为钝角三角形
∠A=55°或125°
圆内接△形状分类
4
△ABC为锐角三角形
已知圆内接△ABC中,AB=AC,圆心O到BC的距离为3cm,圆的半径为6cm,求腰长AB。
练习
△ABC为钝角三角形
AB=6
巩固
练习题
5
已知横截面直径为100cm的圆形下水道,如果水面宽AB为80cm,求下水道中水的最大深度.
如图,AB是圆O的弦,AC是圆O的切线,∠BAC=60° ,则弦AB所对的圆周角等于__________.
已知在直径AB为26的半圆上有一点C,CD⊥AB,垂足为D,且CD=12,求AD的长.
2
1
3
答案
已知横截面直径为100cm的圆形下水道,如果水面宽AB为80cm,求下水道中水的最大深度.
1
20cm或80cm
答案
如图3,AB是圆O的弦,AC是圆O的切线, ∠BAC=60° ,则弦AB所对的圆周角等于__________.
2
60°或120°
答案
已知在直径AB为26的半圆上有一点C,CD⊥AB,垂足为D,且CD=12,求AD的长.
3
8或18
主要内容
12
01
02
03
04
05
点的位置
分类
弦的位置
分类
圆内接△形
状分类
圆周角的位置分类
巩固练习题
答案
已知在直径AB为50的半圆上有一点C,CD⊥AB,垂足为D,且CD=24,求AD的长.
练习
18或32
答案
已知横截面直径为130cm的圆形下水道,如果水面宽AB为120cm,求下水道中水的最大深度.
25cm或90cm
练习
感谢您的聆听!
同课章节目录
