2021-2022学年浙江省各地浙教版数学八年级上册4.2 平面直角坐标系 期末试题分类选编(含解析)
文档属性
| 名称 | 2021-2022学年浙江省各地浙教版数学八年级上册4.2 平面直角坐标系 期末试题分类选编(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 701.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-15 21:32:36 | ||
图片预览


文档简介
4.2 平面直角坐标系
1.(2022·浙江金华·八年级期末)如果在y轴上,那么点P的坐标是
A. B. C. D.
2.(2022·浙江绍兴·八年级期末)在平面直角坐标系的第四象限内有一点M,到x轴的距离为4,到y轴的距离为5,则点M的坐标为( )
A. B. C. D.
3.(2022·浙江绍兴·八年级期末)在平面直角坐标系中,点A的坐标为,点B的坐标为(4,3),则线段AB上任意一点的坐标可表示为( )
A. B.
C. D.
4.(2022·浙江宁波·八年级期末)在平面直角坐标系xOy中,点M(﹣4,3)到x轴的距离是( )
A.﹣4 B.4 C.5 D.3.
5.(2022·浙江衢州·八年级期末)已知点P的坐标为(﹣2,3),则点P到y轴的距离为( )
A.2 B.3 C.5 D.
6.(2022·浙江嘉兴·八年级期末)平面直角坐标系中,点到y轴的距离是( )
A.1 B.2 C.3 D.4
7.(2022·浙江金华·八年级期末)点P( 5,3)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.(2022·浙江衢州·八年级期末)在平面直角坐标系中,点(1,2)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.(2022·浙江丽水·八年级期末)在直角坐标系中,下列点中在第四象限的是( )
A.(﹣1,2) B.(3,2) C.(2,﹣3) D.(﹣2,﹣3)
10.(2022·浙江衢州·八年级期末)已知点P(2﹣m,m﹣5)在第三象限,则整数m的值是( )
A.4 B.3,4 C.4,5 D.2,3,4
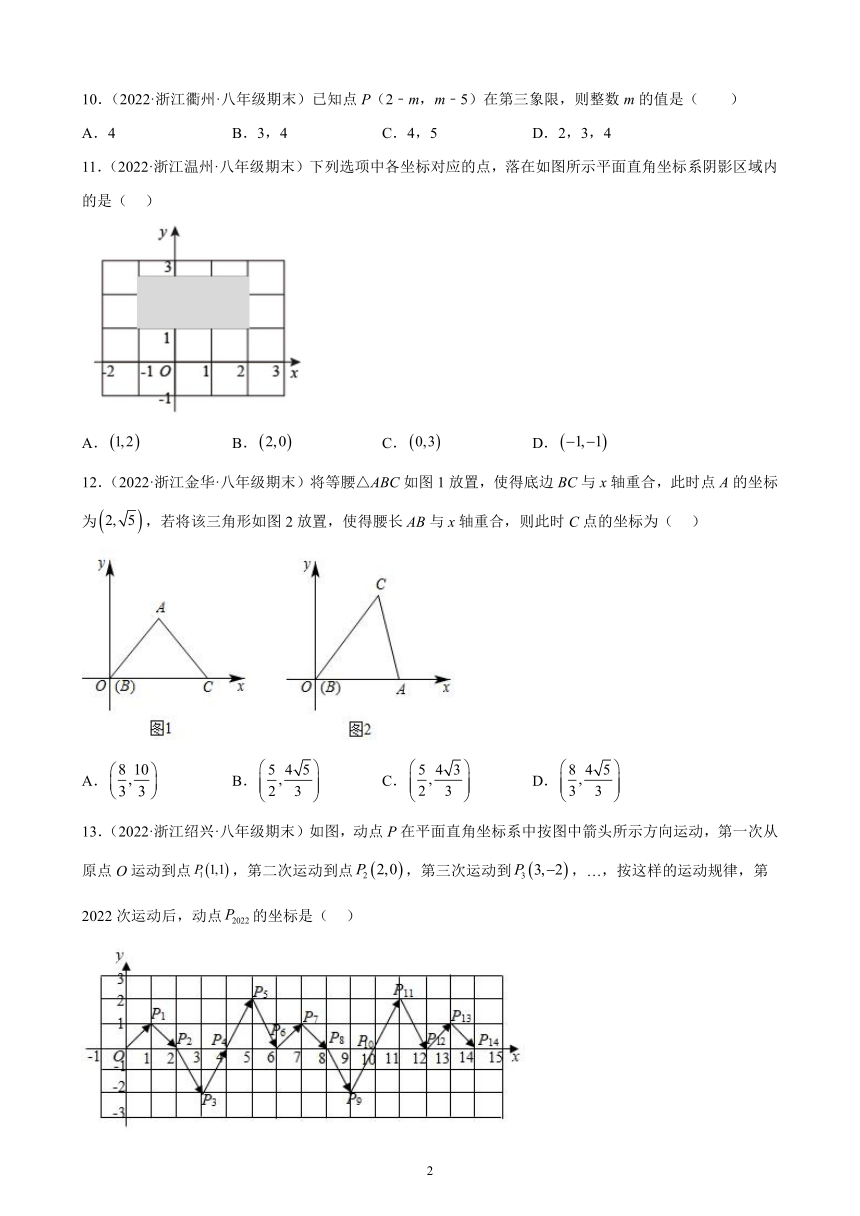
11.(2022·浙江温州·八年级期末)下列选项中各坐标对应的点,落在如图所示平面直角坐标系阴影区域内的是( )
A. B. C. D.
12.(2022·浙江金华·八年级期末)将等腰△ABC如图1放置,使得底边BC与x轴重合,此时点A的坐标为,若将该三角形如图2放置,使得腰长AB与x轴重合,则此时C点的坐标为( )
A. B. C. D.
13.(2022·浙江绍兴·八年级期末)如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第一次从原点O运动到点,第二次运动到点,第三次运动到,…,按这样的运动规律,第2022次运动后,动点的坐标是( )
A. B. C. D.
14.(2022·浙江嘉兴·八年级期末)小嘉去电影院观看《长津湖》,如果用表示5排7座,那么小嘉坐在7排8座可表示为( )
A. B. C. D.
15.(2022·浙江金华·八年级期末)2022年第19届亚运会将在浙江杭州举行,金华将作为亚运会的分会场.以下表示金华市地理位置最合理的是( )
A.距离杭州市200公里 B.在浙江省
C.在杭州市的西南方 D.东经119.65°,北纬29.08°
16.(2022·浙江杭州·八年级期末)若点在x轴上,写出一组符合题意的m,n的值______.
17.(2022·浙江绍兴·八年级期末)点M(﹣3,4)到y轴的距离是__.
18.(2022·浙江湖州·八年级期末)在平面直角坐标系中,若点在y轴上,则m的值是____________.
19.(2022·浙江宁波·八年级期末)点M(a+b,ab)在第二象限,那么点N(a,b)在第_______象限.
20.(2022·浙江宁波·八年级期末)已知点在y轴上,那么_______.
21.(2022·浙江绍兴·八年级期末)若点M(a-2,2a+3)是y轴上的点,则a的值是________.
22.(2022·浙江舟山·八年级期末)在平面直角坐标系中,A(2,0),B(0,4),过点B作直线lx轴,点P(a,4)是线l上的动点,以AP为边在AP右侧作等腰Rt APQ,使∠APQ=90°.
(1)当a=0时,则点Q的坐标是____________.
(2)当点P在直线1上运动时,点Q也随之运动,则OQ的最小值是________________.
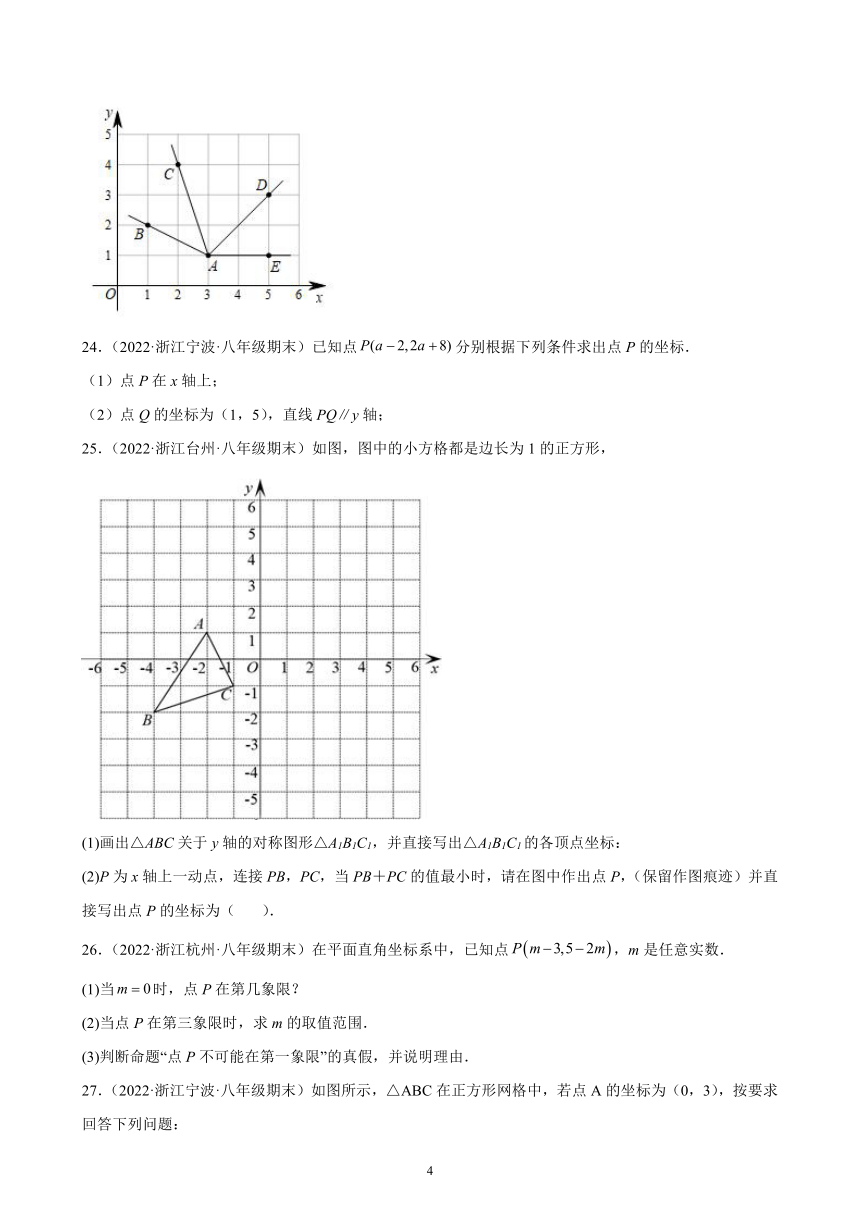
23.(2022·浙江杭州·八年级期末)如图,以点为端点的四条射线AB,AC,AD,AE分别过四点,它们依次是,,,,则______(填或“>”、“=”或“<”)
24.(2022·浙江宁波·八年级期末)已知点分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点Q的坐标为(1,5),直线PQ∥y轴;
25.(2022·浙江台州·八年级期末)如图,图中的小方格都是边长为1的正方形,
(1)画出△ABC关于y轴的对称图形△A1B1C1,并直接写出△A1B1C1的各顶点坐标:
(2)P为x轴上一动点,连接PB,PC,当PB+PC的值最小时,请在图中作出点P,(保留作图痕迹)并直接写出点P的坐标为( ).
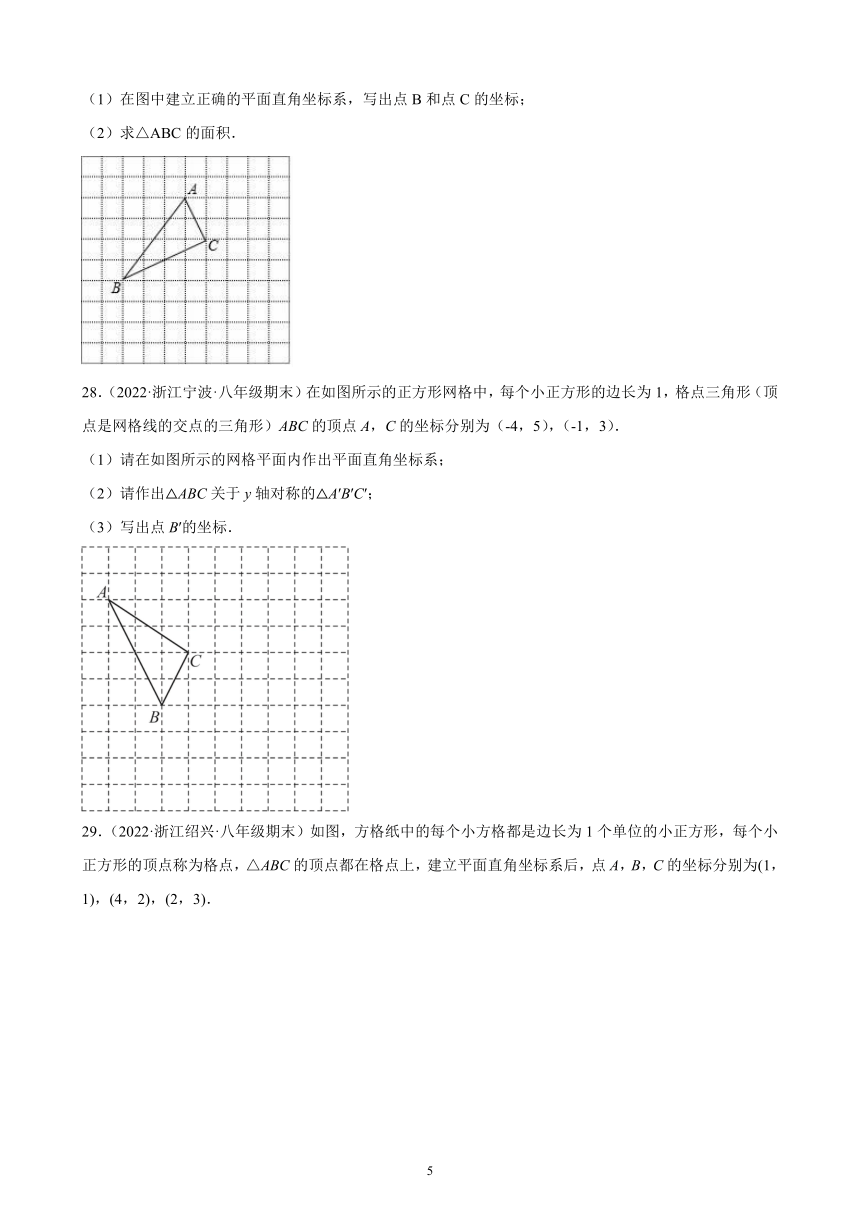
26.(2022·浙江杭州·八年级期末)在平面直角坐标系中,已知点,m是任意实数.
(1)当时,点P在第几象限?
(2)当点P在第三象限时,求m的取值范围.
(3)判断命题“点P不可能在第一象限”的真假,并说明理由.
27.(2022·浙江宁波·八年级期末)如图所示,△ABC在正方形网格中,若点A的坐标为(0,3),按要求回答下列问题:
(1)在图中建立正确的平面直角坐标系,写出点B和点C的坐标;
(2)求△ABC的面积.
28.(2022·浙江宁波·八年级期末)在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A′B′C′;
(3)写出点B′的坐标.
29.(2022·浙江绍兴·八年级期末)如图,方格纸中的每个小方格都是边长为1个单位的小正方形,每个小正方形的顶点称为格点,△ABC的顶点都在格点上,建立平面直角坐标系后,点A,B,C的坐标分别为(1,1),(4,2),(2,3).
(1)画出△ABC向左平移4个单位,再向上平移1个单位后得到的△A1B1C1;
(2)画出△ABC向关于x轴对称的△A2B2C2;
(3)以点A、A1、A2为顶点的三角形的面积为______.
30.(2022·浙江温州·八年级期末)在平面直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的三角形为整点三角形.如图,已知整点,,请在所给的网格区域(含边界)按要求画整点三角形.
(1)在图1中画一个使点C的横、纵坐标的平方和等于25.
(2)在图2中画一个使点D的横、纵坐标之和等于4,且点A在的内部.
参考答案:
1.B
【解析】根据点在y轴上,可知P的横坐标为0,即可得m的值,再确定点P的坐标即可.
解:∵在y轴上,
∴
解得,
∴点P的坐标是(0,-2).
故选B.
解决本题的关键是记住y轴上点的特点:横坐标为0.
2.D
【解析】根据点到坐标轴的距离及点所在的象限解答即可.
解:设点M的坐标为(x,y),
∵点M到x轴的距离为4,
∴,
∴,
∵点M到y轴的距离为5,
∴,
∴,
∵点M在第四象限内,
∴x=5,y=-4,
即点M的坐标为(5,-4).
故选:D.
此题考查平面直角坐标系中的点到坐标轴的距离,象限内点的坐标的符号特点等,其中要牢记第四象限内的点的坐标符号特点为(+,-).
3.A
【解析】根据点的坐标可得轴,结合图形及平行线即可得出线段AB上的点的表示方法.
解:点,点,
可得轴,
得出线段AB上的点表示为,
故选:A.
题目主要考查坐标系中点的特点及平行于x轴的点的特点,理解坐标系中点的特点是解题关键.
4.D
【解析】根据各象限内点的坐标特征与点到x轴的距离等于纵坐标的绝对值解答.
解:点M(-4,3)在第二象限,到x轴的距离是3.
故选:D.
本题考查了各象限内点的坐标的符号特征,记住点到x轴的距离等于纵坐标的绝对值是解决的关键.
5.A
【解析】若点 则到轴的距离为 到轴的距离为 从而可得答案.
解:点P的坐标为(﹣2,3),则点P到y轴的距离为
故选A
本题考查的是点到坐标轴的距离,掌握“点的坐标与点到轴的距离的联系”是解本题的关键.
6.A
【解析】根据点到轴的距离是横坐标的绝对值,可得答案.
解:∵,
∴点到轴的距离是
故选:A
本题考查的是点到坐标轴的距离,掌握点到轴的距离是横坐标的绝对值是解题的关键.
7.B
【解析】根据各象限内点的坐标符号可得其所在象限.
解:∵点P的坐标为(-5,3),
∴点P的横坐标为负数,纵坐标为正数,
∴点P在第二象限,
故选:B.
本题主要考查点的坐标,解题的关键是掌握四个象限内点的坐标符号特点.四个象限的符号分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
8.A
【解析】本题考查了各象限内点的坐标的符号特征,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).
解:点(1,2)横坐标为正,纵坐标为正,
故点(1,2)在第一象限.
故选:A.
9.C
【解析】根据各象限内点的坐标特征对各选项分析判断后利用排除法求解.
解:A.(-1,2)在第二象限,故本选项不合题意;
B.(3,2)在第一象限,故本选项不合题意;
C.(2,-3)在第四象限,故本选项符合题意;
D.(-2,-3)在第三象限,故本选项不合题意.
故选:C.
本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
10.B
【解析】根据第三象限点的坐标特点列不等式组求出解集,再结合整数的定义解答即可.
解:∵P(2﹣m,m﹣5)在第三象限
∴ ,解答2<m<5
∵m是整数
∴m的值为3,4.
故选B.
本题主要考查了平面直角坐标系内点的坐标特点、解不等式组等知识点,掌握第三象限内的点横、纵坐标均小于零成为解答本题的关键.
11.A
【解析】分别描出四个选项中点的坐标在坐标系中的位置,然后判断即可.
解:如图所示,点A(1,2),点B(2,0),点C(0,3),点D(-1,-1),
∴落在阴影区域内的点只有点A(1,2),
故选A.
本题主要考查了在坐标系中描点,解题的关键在于能够熟练掌握平面直角坐标系的相关知识.
12.D
【解析】如图1所示,过点A作交x轴于D,根据点A的坐标得,,根据勾股定理得,根据等腰三角形的性质得,,如图2所示,过点C作交x轴于E,设,则,在中,根据勾股定理得,在中,根据勾股定理得,,解得,则,即可得.
解:如图1所示,过点A作交x轴于D,
∵点A的坐标为,
∴,,
根据勾股定理得,,
∵是等腰三角形,
∴,,
如图2所示,过点C作交x轴于E,
设,则,
在中,,
在中,根据勾股定理得,
,
,
,
,
∴,
∴点C的坐标为,
故选D.
本题考查了等腰三角形的性质,勾股定理,解题的关键是掌握这些知识点.
13.D
【解析】观察图象,结合动点P第一次从原点O运动到点P1(1,1),第二次运动到点P2(2,0),第三次运动到P3(3,﹣2),第四次运动到P4(4,0),第五运动到P5(5,2),第六次运动到P6(6,0),…,结合运动后的点的坐标特点,分别得出点P运动的纵坐标的规律,再根据循环规律可得答案.
解:观察图象,结合动点P第一次从原点O运动到点P1(1,1),第二次运动到点P2(2,0),第三次运动到P3(3,﹣2),第四次运动到P4(4,0),第五运动到P5(5,2),第六次运动到P6(6,0),…,结合运动后的点的坐标特点,
可知由图象可得纵坐标每6次运动组成一个循环:1,0,﹣2,0,2,0;
∵2022÷6=337,
∴经过第2022次运动后,动点P的纵坐标是0,
故选:D.
本题考查了规律型点的坐标,数形结合并从图象中发现循环规律是解题的关键.
14.B
【解析】根据题意可知“坐标的第一个数表示排,第二个数表示座”,然后用坐标表示出小嘉的位置即可.
解:∵用表示5排7座
∴坐标的第一个数表示排,第二个数表示座
∴小嘉坐在7排8座可表示出(7,8).
故选B.
本题主要考查了坐标的应用,根据题意得知“坐标的第一个数表示排,第二个数表示座”是解得本题的关键.
15.D
【解析】根据点的坐标的定义,确定一个位置需要两个数据解答即可.
解:能够准确表示金华市这个地点位置的是:东经119.65°,北纬29.08°
故选D
本题考查了坐标确定位置,是基础题,理解坐标的定义是解题的关键.
16.(答案不唯一)
【解析】根据轴上点的坐标特点,纵坐标为0,即可求解.
解:根据轴上点的坐标特点,纵坐标为零即可,即,
取,
即在x轴上,
故答案是:(答案不唯一).
本题考查了轴上点的坐标特点,解题的关键是掌握在轴上点的坐标的纵坐标为0.
17.3
【解析】根据点到y轴的距离是点的横坐标的绝对值,可得答案.
解:点A的坐标(﹣3,4),它到y轴的距离为|﹣3|=3,
故答案为:3.
本题考查了点的坐标,点到y轴的距离是点的横坐标的绝对值,点到x轴的距离是点的纵坐标的绝对值.
18.-3
【解析】根据y轴上的点的特点为,横坐标=0求解即可.
解:∵点在y轴上,
∴
故答案为:
本题考查了y轴上的点的特点,掌握y轴上的点的特点是解题的关键.
19.三
试题分析:∵点M(a+b,ab)在第二象限,
∴ab>0,a+b<0,
∵ab>0,
∴a、b同号,
∵a+b<0,
∴a<0,b<0,
∴点(a,b)在第三象限.
故答案是三.
考点:点的坐标.
20.3
【解析】根据y轴上点的横坐标为0列式计算即可得解.
解:∵点A(a-3,1-2a)在y轴上,
∴a-3=0,
解得:a=3,
故答案为:3.
本题考查了点的坐标,熟记y轴上点的横坐标为0是解题的关键.
21.2
【解析】根据y轴上的点的横坐标为0即可解答.
∵点M(a-2,2a+3)是y轴上的点,
∴点M的横坐标是0,即a-2=0,
解得:a=2 .
故答案为2 .
本题主要考查了点的坐标,熟知x轴上的点的纵坐标为0,y轴上的点的横坐标为0是解决问题的关键.
22. (4,6)
【解析】(1)过点P作PE⊥OA,垂足为E,过点Q作QF⊥BP,垂足为F,证明△PEA≌△PFQ(AAS),得到PE=PF,EA=QF,然后利用a=0代入可推导Q的坐标;
(2)先根据全等三角形的性质,用a表示Q的坐标,然后用两点距离公式表示OQ2,最后求解最小值即可.
解:(1)如图所示:过点P作PE⊥OA,垂足为E,过点Q作QF⊥BP,垂足为F,
∵BP∥OA,PE⊥OA,
∴∠EPF=∠PEO=90°,
∵∠APQ=90°,
∴∠EPA=∠FPQ=90°﹣∠APF,
在△PEA和△PFQ中,
,
∴△PEA≌△PFQ(AAS),
∴PE=PF,EA=QF,
∵a=0,
∴P(0,4),
∴OE=BP=0,PE=4,
∵A(2,0),
∴OA=2,
∴EA=2,
∴PF=4,QF=AE=2,
∴点Q的坐标为(4,6).
故答案为:(4,6).
(2)∵点P的坐标是(a,4),
∴PE=4,
∵△PEA≌△PFQ,
∴PE=PF=4,EA=QF=2﹣a,
∴Q的坐标为(a+4,6﹣a),
∴OQ2=(a+4)2+(6﹣a)2=2(a﹣1)2+50,
∴a=1时,OQ最小==.
故答案为:.
此题主要考查了平面直角坐标系和三角形的结合、全等三角形的判定和性质、勾股定理等知识,作出辅助线利用线段相等去求点的坐标是解题的关键.
23.=
【解析】在直角坐标系中构造直角三角形,根据三角形边之间的关系推出角之间的关系.
解:连接BC,
∵B(1,2),C(2,4),D(5,3),E(5,1),
∴AE=DE=2,
∴△ADE是等腰直角三角形,
∴∠DAE=45°,
又∵AB=,
同理可得BC=,
AC=,
则在△ABC中,有AB2+BC2=AC2,
∴△ABC是等腰直角三角形,
∴∠BAC=45°,
∴∠BAC=∠DAE,
故答案为:=.
本题考查了坐标与图形的性质,等腰直角三角形的判定,勾股定理及其逆定理,对于直角三角形的判定可以根据各个点的坐标,求出各线段的长度来实现,然后再根据边来判断角的大小.其解题关键在于构造相关的直角三角形.
24.(1);(2)
【解析】(1)根据点在数轴上的特点,令,即可求得,进而求得的坐标;
(2)根据平行与轴的直线的特点,令,即可求得,进而求得的坐标;
(1)点P在x轴上,
,
点P的坐标
(2)点Q的坐标为(1,5),直线PQ∥y轴,
解得
点P的坐标
本题考查了平面直角坐标系中坐标轴上的点的坐标特点,掌握以上知识是解题的关键.
25.(1)见解析,A1 (2,1),B1 (4,-2),C1 (1,-1)
(2)见解析,点P的坐标为(-2,0)
【解析】(1)根据轴对称的性质即可画出△ABC关于y轴的对称图形△A1B1C1,并直接写出△A1B1C1的各顶点坐标;
(2)在坐标系内找到点B关于x轴的对称点B′,连接B′C交x轴于点P即可.
(1)
解:如图,△A1B1C1即为所求;A1(2,1),B1(4,-2),C1(1,-1);
(2)
解:如图,点P即为所求;点P的坐标(-2,0).
故答案为:(-2,0).
本题考查了作图-轴对称变换,点的坐标,轴对称-最短路线问题,解决本题的关键是掌握轴对称的性质.
26.(1),点P在第二象限;
(2)<m<3;
(3)真命题,理由见解析
【解析】(1)求得点P坐标即可得出所在的象限;
(2)根据第三象限的点(x,y)满足x<0,y<0列出关于m的不等式组,解之即可求解;
(3)分点P的横坐标大于0、横坐标等于0和横坐标小于0求解判断即可.
(1)
解:当m=0时,点P坐标为(-3,5),
∴点P在第二象限;
(2)
解:∵点P在第三象限,
∴,
解得:<m<3;
(3)
解:“点P不可能在第一象限”是真命题,理由为:
当m-3>0时,m>3,
∴-2m<-6,即5-2m<-1<0,
∴点P在第四象限;
当m-3=0时,m=3,
∴5-2m=-1,即点P坐标为(0,-1),
∴点P在y轴的负半轴;
当m-3<0时,m<3,即-2m>-6,
∴5-2m>-1,
∴点P在第二象限或第三象限,
综上,点P不可能在第一象限,是真命题.
本题考查点所在的象限、解一元一次不等式(组),熟记象限内点的坐标的符号特点是解答的关键.
27.(1)点B的坐标是(﹣3,﹣1),点C的坐标为(1,1);(2)5.
【解析】(1)根据点A的坐标为(0,3),得出原点的位置,进而建立正确的平面直角坐标系;根据平面直角坐标系直接得出点B和点C的坐标;
(2)借助网格图得出各个边的长度,即可算出周长,根据各边长度的关系,证得△ABC是直角三角形,即可求出面积.
解:(1)如右图所示,
点B的坐标是(﹣3,﹣1),点C的坐标为(1,1);
(2)由图可得,
△ABC的面积是:4×4﹣=5.
本题考查平面直角坐标系的相关概念和面积计算,学会综合运用是关键.
28.(1)(2)如图,(3)B′(2,1).
【解析】(1)易得y轴在C的右边一个单位,x轴在C的下方3个单位;
(2)作出A,B,C三点关于y轴对称的三点,顺次连接即可;
(3)根据所在象限及距离坐标轴的距离可得相应坐标.
解:(1)如图;
(2)如图;
(3)点B′的坐标为(2,1).
29.(1)见解析
(2)见解析
(3)4
【解析】(1)直接利用平移的性质得出对应点位置进而得出答案;
(2)直接利用轴对称图形的性质得出对应点位置进而得出答案;
(3)利用三角形面积公式求出答案.
(1)
解:如图所示:△A1B1C1,即为所求;
(2)
解:如图所示:△A2B2C2,即为所求;
(3)
解:以点A、A1、A2为顶点的三角形的面积为:×2×4=4.
故答案为:4.
本题主要考查了轴对称变换以及平移变换和三角形面积求法,正确得出对应点位置是解题关键.
30.(1)见解析
(2)见解析
【解析】(1)根据题意画图即可;
(2)根据题意画图即可;
(1)
解:(1)画法不唯一,如下图.
(2)
画法不唯一,如下图.
本题考查网格作图、平面直角坐标系等知识,是基础考点,掌握相关知识是解题关键.
1.(2022·浙江金华·八年级期末)如果在y轴上,那么点P的坐标是
A. B. C. D.
2.(2022·浙江绍兴·八年级期末)在平面直角坐标系的第四象限内有一点M,到x轴的距离为4,到y轴的距离为5,则点M的坐标为( )
A. B. C. D.
3.(2022·浙江绍兴·八年级期末)在平面直角坐标系中,点A的坐标为,点B的坐标为(4,3),则线段AB上任意一点的坐标可表示为( )
A. B.
C. D.
4.(2022·浙江宁波·八年级期末)在平面直角坐标系xOy中,点M(﹣4,3)到x轴的距离是( )
A.﹣4 B.4 C.5 D.3.
5.(2022·浙江衢州·八年级期末)已知点P的坐标为(﹣2,3),则点P到y轴的距离为( )
A.2 B.3 C.5 D.
6.(2022·浙江嘉兴·八年级期末)平面直角坐标系中,点到y轴的距离是( )
A.1 B.2 C.3 D.4
7.(2022·浙江金华·八年级期末)点P( 5,3)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.(2022·浙江衢州·八年级期末)在平面直角坐标系中,点(1,2)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.(2022·浙江丽水·八年级期末)在直角坐标系中,下列点中在第四象限的是( )
A.(﹣1,2) B.(3,2) C.(2,﹣3) D.(﹣2,﹣3)
10.(2022·浙江衢州·八年级期末)已知点P(2﹣m,m﹣5)在第三象限,则整数m的值是( )
A.4 B.3,4 C.4,5 D.2,3,4
11.(2022·浙江温州·八年级期末)下列选项中各坐标对应的点,落在如图所示平面直角坐标系阴影区域内的是( )
A. B. C. D.
12.(2022·浙江金华·八年级期末)将等腰△ABC如图1放置,使得底边BC与x轴重合,此时点A的坐标为,若将该三角形如图2放置,使得腰长AB与x轴重合,则此时C点的坐标为( )
A. B. C. D.
13.(2022·浙江绍兴·八年级期末)如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第一次从原点O运动到点,第二次运动到点,第三次运动到,…,按这样的运动规律,第2022次运动后,动点的坐标是( )
A. B. C. D.
14.(2022·浙江嘉兴·八年级期末)小嘉去电影院观看《长津湖》,如果用表示5排7座,那么小嘉坐在7排8座可表示为( )
A. B. C. D.
15.(2022·浙江金华·八年级期末)2022年第19届亚运会将在浙江杭州举行,金华将作为亚运会的分会场.以下表示金华市地理位置最合理的是( )
A.距离杭州市200公里 B.在浙江省
C.在杭州市的西南方 D.东经119.65°,北纬29.08°
16.(2022·浙江杭州·八年级期末)若点在x轴上,写出一组符合题意的m,n的值______.
17.(2022·浙江绍兴·八年级期末)点M(﹣3,4)到y轴的距离是__.
18.(2022·浙江湖州·八年级期末)在平面直角坐标系中,若点在y轴上,则m的值是____________.
19.(2022·浙江宁波·八年级期末)点M(a+b,ab)在第二象限,那么点N(a,b)在第_______象限.
20.(2022·浙江宁波·八年级期末)已知点在y轴上,那么_______.
21.(2022·浙江绍兴·八年级期末)若点M(a-2,2a+3)是y轴上的点,则a的值是________.
22.(2022·浙江舟山·八年级期末)在平面直角坐标系中,A(2,0),B(0,4),过点B作直线lx轴,点P(a,4)是线l上的动点,以AP为边在AP右侧作等腰Rt APQ,使∠APQ=90°.
(1)当a=0时,则点Q的坐标是____________.
(2)当点P在直线1上运动时,点Q也随之运动,则OQ的最小值是________________.
23.(2022·浙江杭州·八年级期末)如图,以点为端点的四条射线AB,AC,AD,AE分别过四点,它们依次是,,,,则______(填或“>”、“=”或“<”)
24.(2022·浙江宁波·八年级期末)已知点分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点Q的坐标为(1,5),直线PQ∥y轴;
25.(2022·浙江台州·八年级期末)如图,图中的小方格都是边长为1的正方形,
(1)画出△ABC关于y轴的对称图形△A1B1C1,并直接写出△A1B1C1的各顶点坐标:
(2)P为x轴上一动点,连接PB,PC,当PB+PC的值最小时,请在图中作出点P,(保留作图痕迹)并直接写出点P的坐标为( ).
26.(2022·浙江杭州·八年级期末)在平面直角坐标系中,已知点,m是任意实数.
(1)当时,点P在第几象限?
(2)当点P在第三象限时,求m的取值范围.
(3)判断命题“点P不可能在第一象限”的真假,并说明理由.
27.(2022·浙江宁波·八年级期末)如图所示,△ABC在正方形网格中,若点A的坐标为(0,3),按要求回答下列问题:
(1)在图中建立正确的平面直角坐标系,写出点B和点C的坐标;
(2)求△ABC的面积.
28.(2022·浙江宁波·八年级期末)在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A′B′C′;
(3)写出点B′的坐标.
29.(2022·浙江绍兴·八年级期末)如图,方格纸中的每个小方格都是边长为1个单位的小正方形,每个小正方形的顶点称为格点,△ABC的顶点都在格点上,建立平面直角坐标系后,点A,B,C的坐标分别为(1,1),(4,2),(2,3).
(1)画出△ABC向左平移4个单位,再向上平移1个单位后得到的△A1B1C1;
(2)画出△ABC向关于x轴对称的△A2B2C2;
(3)以点A、A1、A2为顶点的三角形的面积为______.
30.(2022·浙江温州·八年级期末)在平面直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的三角形为整点三角形.如图,已知整点,,请在所给的网格区域(含边界)按要求画整点三角形.
(1)在图1中画一个使点C的横、纵坐标的平方和等于25.
(2)在图2中画一个使点D的横、纵坐标之和等于4,且点A在的内部.
参考答案:
1.B
【解析】根据点在y轴上,可知P的横坐标为0,即可得m的值,再确定点P的坐标即可.
解:∵在y轴上,
∴
解得,
∴点P的坐标是(0,-2).
故选B.
解决本题的关键是记住y轴上点的特点:横坐标为0.
2.D
【解析】根据点到坐标轴的距离及点所在的象限解答即可.
解:设点M的坐标为(x,y),
∵点M到x轴的距离为4,
∴,
∴,
∵点M到y轴的距离为5,
∴,
∴,
∵点M在第四象限内,
∴x=5,y=-4,
即点M的坐标为(5,-4).
故选:D.
此题考查平面直角坐标系中的点到坐标轴的距离,象限内点的坐标的符号特点等,其中要牢记第四象限内的点的坐标符号特点为(+,-).
3.A
【解析】根据点的坐标可得轴,结合图形及平行线即可得出线段AB上的点的表示方法.
解:点,点,
可得轴,
得出线段AB上的点表示为,
故选:A.
题目主要考查坐标系中点的特点及平行于x轴的点的特点,理解坐标系中点的特点是解题关键.
4.D
【解析】根据各象限内点的坐标特征与点到x轴的距离等于纵坐标的绝对值解答.
解:点M(-4,3)在第二象限,到x轴的距离是3.
故选:D.
本题考查了各象限内点的坐标的符号特征,记住点到x轴的距离等于纵坐标的绝对值是解决的关键.
5.A
【解析】若点 则到轴的距离为 到轴的距离为 从而可得答案.
解:点P的坐标为(﹣2,3),则点P到y轴的距离为
故选A
本题考查的是点到坐标轴的距离,掌握“点的坐标与点到轴的距离的联系”是解本题的关键.
6.A
【解析】根据点到轴的距离是横坐标的绝对值,可得答案.
解:∵,
∴点到轴的距离是
故选:A
本题考查的是点到坐标轴的距离,掌握点到轴的距离是横坐标的绝对值是解题的关键.
7.B
【解析】根据各象限内点的坐标符号可得其所在象限.
解:∵点P的坐标为(-5,3),
∴点P的横坐标为负数,纵坐标为正数,
∴点P在第二象限,
故选:B.
本题主要考查点的坐标,解题的关键是掌握四个象限内点的坐标符号特点.四个象限的符号分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
8.A
【解析】本题考查了各象限内点的坐标的符号特征,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).
解:点(1,2)横坐标为正,纵坐标为正,
故点(1,2)在第一象限.
故选:A.
9.C
【解析】根据各象限内点的坐标特征对各选项分析判断后利用排除法求解.
解:A.(-1,2)在第二象限,故本选项不合题意;
B.(3,2)在第一象限,故本选项不合题意;
C.(2,-3)在第四象限,故本选项符合题意;
D.(-2,-3)在第三象限,故本选项不合题意.
故选:C.
本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
10.B
【解析】根据第三象限点的坐标特点列不等式组求出解集,再结合整数的定义解答即可.
解:∵P(2﹣m,m﹣5)在第三象限
∴ ,解答2<m<5
∵m是整数
∴m的值为3,4.
故选B.
本题主要考查了平面直角坐标系内点的坐标特点、解不等式组等知识点,掌握第三象限内的点横、纵坐标均小于零成为解答本题的关键.
11.A
【解析】分别描出四个选项中点的坐标在坐标系中的位置,然后判断即可.
解:如图所示,点A(1,2),点B(2,0),点C(0,3),点D(-1,-1),
∴落在阴影区域内的点只有点A(1,2),
故选A.
本题主要考查了在坐标系中描点,解题的关键在于能够熟练掌握平面直角坐标系的相关知识.
12.D
【解析】如图1所示,过点A作交x轴于D,根据点A的坐标得,,根据勾股定理得,根据等腰三角形的性质得,,如图2所示,过点C作交x轴于E,设,则,在中,根据勾股定理得,在中,根据勾股定理得,,解得,则,即可得.
解:如图1所示,过点A作交x轴于D,
∵点A的坐标为,
∴,,
根据勾股定理得,,
∵是等腰三角形,
∴,,
如图2所示,过点C作交x轴于E,
设,则,
在中,,
在中,根据勾股定理得,
,
,
,
,
∴,
∴点C的坐标为,
故选D.
本题考查了等腰三角形的性质,勾股定理,解题的关键是掌握这些知识点.
13.D
【解析】观察图象,结合动点P第一次从原点O运动到点P1(1,1),第二次运动到点P2(2,0),第三次运动到P3(3,﹣2),第四次运动到P4(4,0),第五运动到P5(5,2),第六次运动到P6(6,0),…,结合运动后的点的坐标特点,分别得出点P运动的纵坐标的规律,再根据循环规律可得答案.
解:观察图象,结合动点P第一次从原点O运动到点P1(1,1),第二次运动到点P2(2,0),第三次运动到P3(3,﹣2),第四次运动到P4(4,0),第五运动到P5(5,2),第六次运动到P6(6,0),…,结合运动后的点的坐标特点,
可知由图象可得纵坐标每6次运动组成一个循环:1,0,﹣2,0,2,0;
∵2022÷6=337,
∴经过第2022次运动后,动点P的纵坐标是0,
故选:D.
本题考查了规律型点的坐标,数形结合并从图象中发现循环规律是解题的关键.
14.B
【解析】根据题意可知“坐标的第一个数表示排,第二个数表示座”,然后用坐标表示出小嘉的位置即可.
解:∵用表示5排7座
∴坐标的第一个数表示排,第二个数表示座
∴小嘉坐在7排8座可表示出(7,8).
故选B.
本题主要考查了坐标的应用,根据题意得知“坐标的第一个数表示排,第二个数表示座”是解得本题的关键.
15.D
【解析】根据点的坐标的定义,确定一个位置需要两个数据解答即可.
解:能够准确表示金华市这个地点位置的是:东经119.65°,北纬29.08°
故选D
本题考查了坐标确定位置,是基础题,理解坐标的定义是解题的关键.
16.(答案不唯一)
【解析】根据轴上点的坐标特点,纵坐标为0,即可求解.
解:根据轴上点的坐标特点,纵坐标为零即可,即,
取,
即在x轴上,
故答案是:(答案不唯一).
本题考查了轴上点的坐标特点,解题的关键是掌握在轴上点的坐标的纵坐标为0.
17.3
【解析】根据点到y轴的距离是点的横坐标的绝对值,可得答案.
解:点A的坐标(﹣3,4),它到y轴的距离为|﹣3|=3,
故答案为:3.
本题考查了点的坐标,点到y轴的距离是点的横坐标的绝对值,点到x轴的距离是点的纵坐标的绝对值.
18.-3
【解析】根据y轴上的点的特点为,横坐标=0求解即可.
解:∵点在y轴上,
∴
故答案为:
本题考查了y轴上的点的特点,掌握y轴上的点的特点是解题的关键.
19.三
试题分析:∵点M(a+b,ab)在第二象限,
∴ab>0,a+b<0,
∵ab>0,
∴a、b同号,
∵a+b<0,
∴a<0,b<0,
∴点(a,b)在第三象限.
故答案是三.
考点:点的坐标.
20.3
【解析】根据y轴上点的横坐标为0列式计算即可得解.
解:∵点A(a-3,1-2a)在y轴上,
∴a-3=0,
解得:a=3,
故答案为:3.
本题考查了点的坐标,熟记y轴上点的横坐标为0是解题的关键.
21.2
【解析】根据y轴上的点的横坐标为0即可解答.
∵点M(a-2,2a+3)是y轴上的点,
∴点M的横坐标是0,即a-2=0,
解得:a=2 .
故答案为2 .
本题主要考查了点的坐标,熟知x轴上的点的纵坐标为0,y轴上的点的横坐标为0是解决问题的关键.
22. (4,6)
【解析】(1)过点P作PE⊥OA,垂足为E,过点Q作QF⊥BP,垂足为F,证明△PEA≌△PFQ(AAS),得到PE=PF,EA=QF,然后利用a=0代入可推导Q的坐标;
(2)先根据全等三角形的性质,用a表示Q的坐标,然后用两点距离公式表示OQ2,最后求解最小值即可.
解:(1)如图所示:过点P作PE⊥OA,垂足为E,过点Q作QF⊥BP,垂足为F,
∵BP∥OA,PE⊥OA,
∴∠EPF=∠PEO=90°,
∵∠APQ=90°,
∴∠EPA=∠FPQ=90°﹣∠APF,
在△PEA和△PFQ中,
,
∴△PEA≌△PFQ(AAS),
∴PE=PF,EA=QF,
∵a=0,
∴P(0,4),
∴OE=BP=0,PE=4,
∵A(2,0),
∴OA=2,
∴EA=2,
∴PF=4,QF=AE=2,
∴点Q的坐标为(4,6).
故答案为:(4,6).
(2)∵点P的坐标是(a,4),
∴PE=4,
∵△PEA≌△PFQ,
∴PE=PF=4,EA=QF=2﹣a,
∴Q的坐标为(a+4,6﹣a),
∴OQ2=(a+4)2+(6﹣a)2=2(a﹣1)2+50,
∴a=1时,OQ最小==.
故答案为:.
此题主要考查了平面直角坐标系和三角形的结合、全等三角形的判定和性质、勾股定理等知识,作出辅助线利用线段相等去求点的坐标是解题的关键.
23.=
【解析】在直角坐标系中构造直角三角形,根据三角形边之间的关系推出角之间的关系.
解:连接BC,
∵B(1,2),C(2,4),D(5,3),E(5,1),
∴AE=DE=2,
∴△ADE是等腰直角三角形,
∴∠DAE=45°,
又∵AB=,
同理可得BC=,
AC=,
则在△ABC中,有AB2+BC2=AC2,
∴△ABC是等腰直角三角形,
∴∠BAC=45°,
∴∠BAC=∠DAE,
故答案为:=.
本题考查了坐标与图形的性质,等腰直角三角形的判定,勾股定理及其逆定理,对于直角三角形的判定可以根据各个点的坐标,求出各线段的长度来实现,然后再根据边来判断角的大小.其解题关键在于构造相关的直角三角形.
24.(1);(2)
【解析】(1)根据点在数轴上的特点,令,即可求得,进而求得的坐标;
(2)根据平行与轴的直线的特点,令,即可求得,进而求得的坐标;
(1)点P在x轴上,
,
点P的坐标
(2)点Q的坐标为(1,5),直线PQ∥y轴,
解得
点P的坐标
本题考查了平面直角坐标系中坐标轴上的点的坐标特点,掌握以上知识是解题的关键.
25.(1)见解析,A1 (2,1),B1 (4,-2),C1 (1,-1)
(2)见解析,点P的坐标为(-2,0)
【解析】(1)根据轴对称的性质即可画出△ABC关于y轴的对称图形△A1B1C1,并直接写出△A1B1C1的各顶点坐标;
(2)在坐标系内找到点B关于x轴的对称点B′,连接B′C交x轴于点P即可.
(1)
解:如图,△A1B1C1即为所求;A1(2,1),B1(4,-2),C1(1,-1);
(2)
解:如图,点P即为所求;点P的坐标(-2,0).
故答案为:(-2,0).
本题考查了作图-轴对称变换,点的坐标,轴对称-最短路线问题,解决本题的关键是掌握轴对称的性质.
26.(1),点P在第二象限;
(2)<m<3;
(3)真命题,理由见解析
【解析】(1)求得点P坐标即可得出所在的象限;
(2)根据第三象限的点(x,y)满足x<0,y<0列出关于m的不等式组,解之即可求解;
(3)分点P的横坐标大于0、横坐标等于0和横坐标小于0求解判断即可.
(1)
解:当m=0时,点P坐标为(-3,5),
∴点P在第二象限;
(2)
解:∵点P在第三象限,
∴,
解得:<m<3;
(3)
解:“点P不可能在第一象限”是真命题,理由为:
当m-3>0时,m>3,
∴-2m<-6,即5-2m<-1<0,
∴点P在第四象限;
当m-3=0时,m=3,
∴5-2m=-1,即点P坐标为(0,-1),
∴点P在y轴的负半轴;
当m-3<0时,m<3,即-2m>-6,
∴5-2m>-1,
∴点P在第二象限或第三象限,
综上,点P不可能在第一象限,是真命题.
本题考查点所在的象限、解一元一次不等式(组),熟记象限内点的坐标的符号特点是解答的关键.
27.(1)点B的坐标是(﹣3,﹣1),点C的坐标为(1,1);(2)5.
【解析】(1)根据点A的坐标为(0,3),得出原点的位置,进而建立正确的平面直角坐标系;根据平面直角坐标系直接得出点B和点C的坐标;
(2)借助网格图得出各个边的长度,即可算出周长,根据各边长度的关系,证得△ABC是直角三角形,即可求出面积.
解:(1)如右图所示,
点B的坐标是(﹣3,﹣1),点C的坐标为(1,1);
(2)由图可得,
△ABC的面积是:4×4﹣=5.
本题考查平面直角坐标系的相关概念和面积计算,学会综合运用是关键.
28.(1)(2)如图,(3)B′(2,1).
【解析】(1)易得y轴在C的右边一个单位,x轴在C的下方3个单位;
(2)作出A,B,C三点关于y轴对称的三点,顺次连接即可;
(3)根据所在象限及距离坐标轴的距离可得相应坐标.
解:(1)如图;
(2)如图;
(3)点B′的坐标为(2,1).
29.(1)见解析
(2)见解析
(3)4
【解析】(1)直接利用平移的性质得出对应点位置进而得出答案;
(2)直接利用轴对称图形的性质得出对应点位置进而得出答案;
(3)利用三角形面积公式求出答案.
(1)
解:如图所示:△A1B1C1,即为所求;
(2)
解:如图所示:△A2B2C2,即为所求;
(3)
解:以点A、A1、A2为顶点的三角形的面积为:×2×4=4.
故答案为:4.
本题主要考查了轴对称变换以及平移变换和三角形面积求法,正确得出对应点位置是解题关键.
30.(1)见解析
(2)见解析
【解析】(1)根据题意画图即可;
(2)根据题意画图即可;
(1)
解:(1)画法不唯一,如下图.
(2)
画法不唯一,如下图.
本题考查网格作图、平面直角坐标系等知识,是基础考点,掌握相关知识是解题关键.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
