全等三角形期末复习课学案

全等三角形复习课
班级________姓名____________
学习目标
1. 通过全等三角形的概念和判定方法的复习，让学生体会辨别、探寻、运用三角形全等的一般方法；
2. 培养学生观察和理解能力，几何语言的叙述能力及运用全等三角形知识解决实际问题的能力.
学习重点
运用全等三角形的识别方法来探寻三角形全等以及运用全等三角形的知识解决实际
一、知识回顾：
1. 全等三角形的定义： .
2．全等三角形的性质： .
3．三角形全等的常用判别方法有： .
4．三角形全等的条件思路：
当两三角形已具备两角对应相等时，第三条件应找 .
当两三角形已具备两边对应相等时，第三条件应找 .
当两三角形已具备一角一边对应相等时，第三条件应找 .
5．找三角形全等的条件时经常见到的隐含条件有： 、 .
6．三个角对应相等的两个三角形全等吗？两边和其中一边的对角对应相等的两个三角形全等吗？试举例说明．
二、例习题：
(一)、全等三角形的概念及其性质
例1.已知如图（1），≌,其中的
对应边:____与____,____与____,____与____,
对应角:_____与_____,____与_____,____与_____.
例2．如图，点D在AB上，点E在AC上，CD与BE相交于点O，
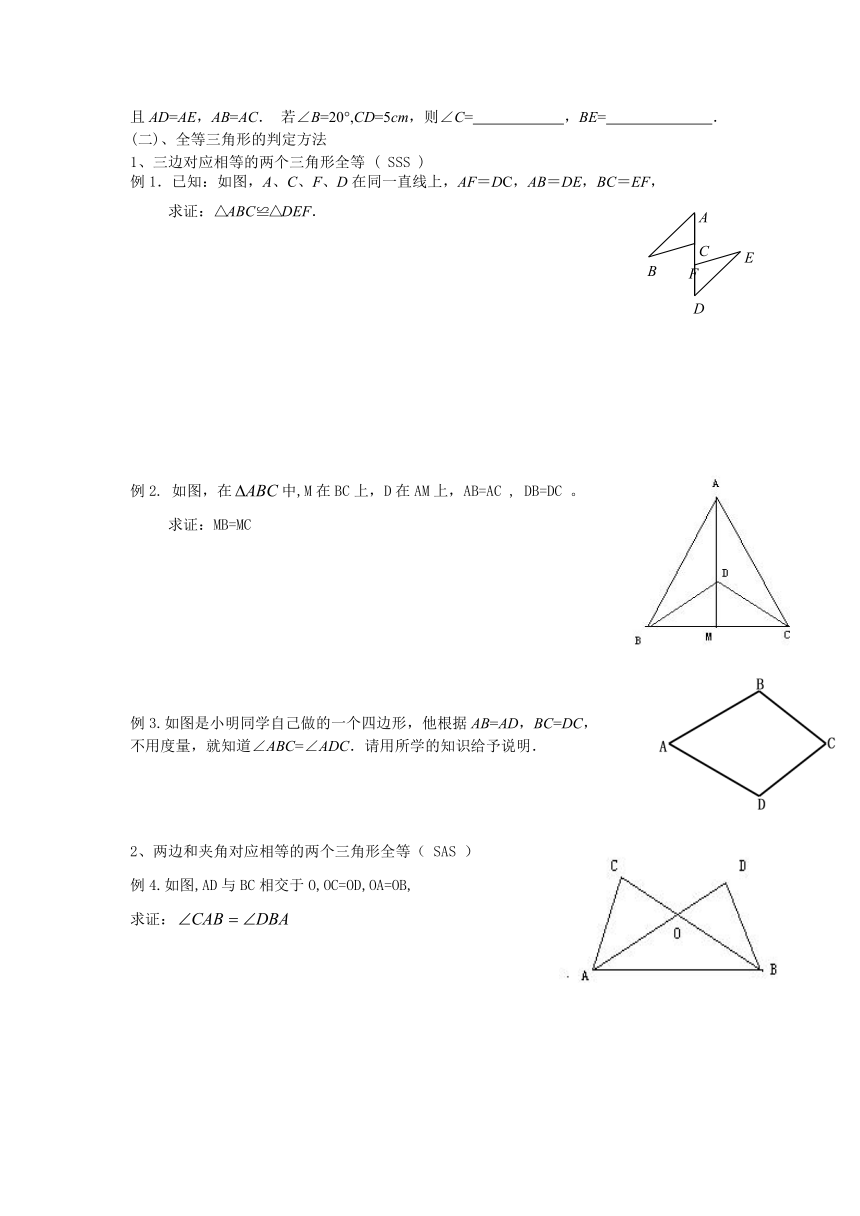
且AD=AE，AB=AC． 若∠B=20°,CD=5cm，则∠C= ，BE= ．
(二)、全等三角形的判定方法
1、三边对应相等的两个三角形全等 ( SSS )
例1．已知：如图，A、C、F、D在同一直线上，AF＝DC，AB＝DE，BC＝EF，
求证：△ABC≌△DEF．
例2. 如图，在中,M在BC上，D在AM上，AB=AC , DB=DC 。
求证：MB=MC
例3.如图是小明同学自己做的一个四边形，他根据AB=AD，BC=DC，
不用度量，就知道∠ABC=∠ADC．请用所学的知识给予说明．
2、两边和夹角对应相等的两个三角形全等（ SAS ）
例4.如图,AD与BC相交于O,OC=OD,OA=OB,
求证：
3、两角和夹边对应相等的两个三角形全等 ( ASA )
例5.如图，梯形ABCD中，AB//CD，E是BC的中点，直线AE交DC的延长线于F
求证：≌
4、两角和夹边对应相等的两个三角形全等 ( AAS )
例6.如图，在中，AB=AC，D、E分别在BC、AC边上。且,AD=DE
求证：≌.
5、一条直角边和斜边对应相等的两个直角三角形全等 ( H L )
例7.如图，在△ABC中，点A在DE上，∠D=∠E=Rt∠,且∠1=∠2， CD=AE，判断AC与AB的关系，并说明理由．
三、角平分线
1、角平分线性质定理：角平分线上的点到这个角两边的距离相等。
2、逆定理： 到一个角两边的距离相等的点在这个角的平分线上。
例8．如图，在中，，平分，
，那么点到直线的距离是　　　　　　cm．
例9．如图，已知在Rt△ABC中，∠C=90°, BD平分∠ABC, 交AC于D.
(1) 若∠BAC=30°, 则AD与BD之间有何数量关系，说明你的理由;
(2) 若AP平分∠BAC，交BD于P, 求∠BPA的度数.
四、尺规作图 ◆尺规作图是指限定用无刻度的直尺而圓規能以一給定點為圓心，過另一個給定點畫出一個圓（當然，這兩種工具都是理想化的。試問哪把尺子能有無限長？）。和圆规作为工具的作图。
例10.如图，已知和射线，用尺规作图法作（要求保留作图痕迹）．
例11． 如图，Rt△ABC中，∠C=90°, ∠CAB=30°, 用圆规和直尺作图，
用两种方法把它分成两个三角形，且其中一个是等腰三角形.（保留作图痕迹，不要求写作法和证明）.
三．巩固练习：
一.选择题
1. 两个三角形只有以下元素对应相等，不能判定两个三角形全等的是（ ）
A. 两角和其中一角的对边 B. 两边及夹角 C. 三个角 D. 三条边
2. 能使两个直角三角形全等的条件是( )
A. 一锐角对应相等 B. 两锐角对应相等 C.一条边对应相等 　D.两直角边对应相等
3. 在△ABC和△A′B′C′中，已知∠A=∠A′，AB= A′B′，在下面判定中错误的是( )
A. 若添加条件AC=A′C′，则△ABC ≌△A′B′C′
B. 若添加条件BC=B′C′，则△ABC ≌△A′B′C′
C. 若添加条件∠B=∠B′，则△ABC ≌△A′B′C′
D. 若添加条件∠C=∠C′，则△ABC ≌△A′B′C′
4. 在△ABC和△A′B′C′中，①AB= A′B′,②BC= B′C′,③AC= A′C′，④∠A=∠A′，⑤∠B=∠B′，⑥∠C=∠C′，则下列条件组不能保证△ABC≌△A′B′C′的是( )
A.①②③ B.①②⑤ C.②④⑤ D.①③⑤
二、解答题
1.如图，点E，F在BC上，BE=CF，AB=DC，∠B=∠C. 证明：∠A=∠D
2.如图，已知AB=AD， ∠B=∠D，∠1=∠2，证明：BC=DE
3、如图， BD=CD，BF⊥AC，CE⊥AB.求证：点D在∠BAC的平分线上.

课外延伸：
等腰直角△ABC，其中AB＝AC，∠BAC＝90°，过B、C作经过A点直线L的垂线，垂足分别为M、N
（1）你能找到一对三角形的全等吗？说明理由．
（2）BM，CN，MN之间有何关系？说明理由
若将直线l旋转到如下图的位置，其他条件不变，那么上题的结论是否依旧成立？说明理由
B
C
D
E
F
A
A
O
B
′