【新课标】1.1 锐角三角函数(1) 课件(共26张PPT)
文档属性
| 名称 | 【新课标】1.1 锐角三角函数(1) 课件(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-20 00:00:00 | ||
图片预览




文档简介
(共26张PPT)
1.1 锐角三角函数(1)
浙教版九年级下册
教学目标
1.理解锐角三角函数的概念,并能将三角函数表示为两条线段的比;
2.了解直角三角形中的两个锐角三角函数值之间的关系;
3.了解直角三角形中的边与三角函数值的关系。
教学重难点
重点:
理解锐角三角函数的概念,并能将三角函数表示为两条线段的比。
难点:
直角三角形中锐角三角函数值与三边之间的关系及求三角函数值。
新知导入
两个物体在倾斜角不同的斜面上向上运动相同的距离,它们上升的高度相同吗?
新知导入
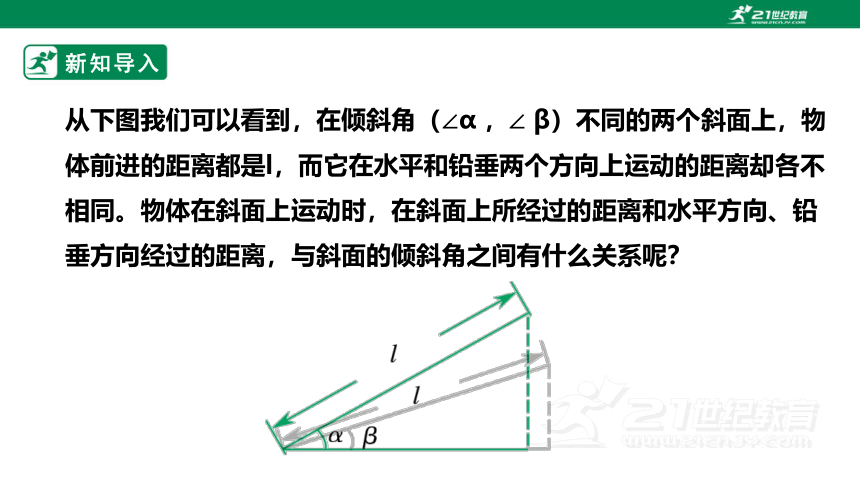
从下图我们可以看到,在倾斜角(∠α ,∠ β)不同的两个斜面上,物体前进的距离都是l,而它在水平和铅垂两个方向上运动的距离却各不相同。物体在斜面上运动时,在斜面上所经过的距离和水平方向、铅垂方向经过的距离,与斜面的倾斜角之间有什么关系呢?
新知讲解
小组合作
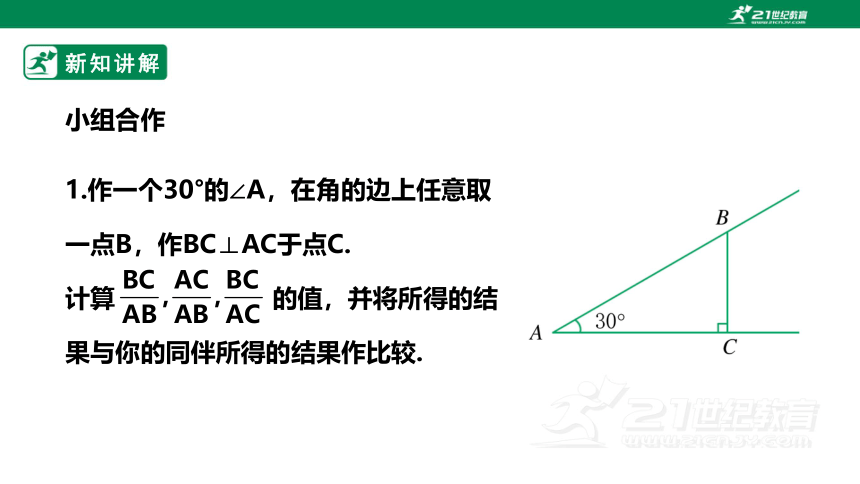
1.作一个30°的∠A,在角的边上任意取一点B,作BC⊥AC于点C.
计算 的值,并将所得的结果与你的同伴所得的结果作比较.
新知讲解
小组合作
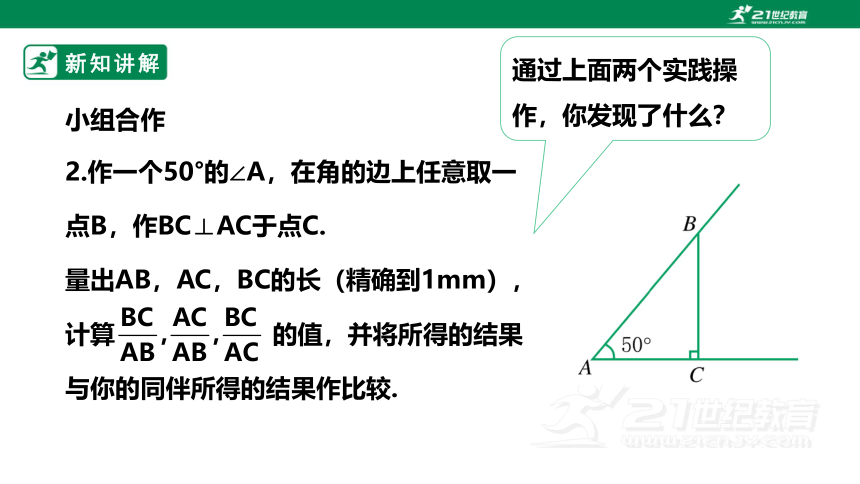
2.作一个50°的∠A,在角的边上任意取一点B,作BC⊥AC于点C.
量出AB,AC,BC的长(精确到1mm),计算 的值,并将所得的结果与你的同伴所得的结果作比较.
通过上面两个实践操作,你发现了什么?
新知讲解
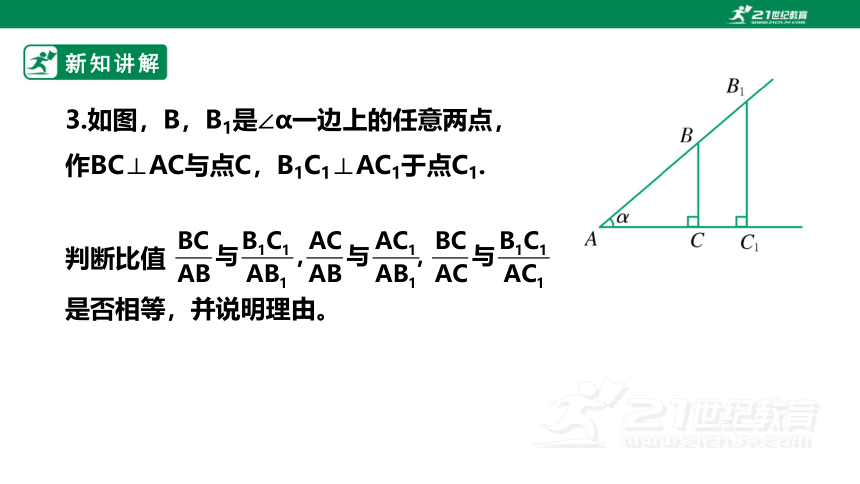
3.如图,B,B1是∠α一边上的任意两点,作BC⊥AC与点C,B1C1⊥AC1于点C1.
判断比值
是否相等,并说明理由。
新知讲解
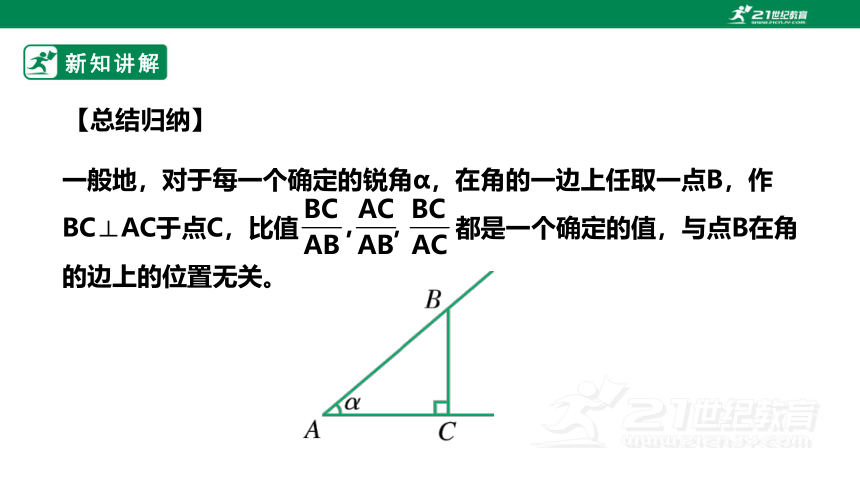
一般地,对于每一个确定的锐角α,在角的一边上任取一点B,作BC⊥AC于点C,比值 都是一个确定的值,与点B在角的边上的位置无关。
【总结归纳】
新知讲解
而当锐角α变化时,比值 都发生了变化,因此,我们把比值 看做是关于锐角α的函数。
比值 叫做∠α的正弦,记作sinα,即sin α=
新知讲解
比值 叫做∠α的余弦,记作cosα,即cos α=
比值 叫做∠α的正切,记作tanα,即tan α=
注意:sinα,cosα,tanα都是一个完整的符号,单独的“sin”没有意义。
其中α前面的“∠"一般省略不写.
新知讲解
锐角α的正弦、余弦和正切统称∠α的三角函数。
如果∠ A是Rt△的一个锐角,则有
新知讲解
师:根据上面的三角函数定义,你知道正弦与余弦三角函数值的取值范围吗?
∴ 0分析:直角三角形中,斜边大于直角边.
新知讲解
【例1】如图,在Rt△ABC中,∠C=Rt∠,AB=5,BC=3.
求∠A的正弦、余弦和正切.
解:如图,在Rt△ABC中,AB=5,BC=3,
新知讲解
【拓展延伸】如图,在Rt△ABC中,∠C=Rt∠,AB=5,BC=3.
你能求出∠B的正弦、余弦和正切吗?
解:如图,在Rt△ABC中,AB=5,BC=3,
新知讲解
【思考】观察以上的计算结果,你发现了什么?
总结:
在同一个直角三角形中,sin A=cos B.
cos A=sin B,
tan A · tan B=1.
课堂练习
1. 在△ABC中,∠C = 90°,AB = 7,BC = 3,则 sinA 的值为 ( )
A. B.
C. D.
C
课堂练习
2. sin70°,cos70°,tan70° 的大小关系是 ( )
A. tan70°<cos70°<sin70°
B. cos70°<tan70°<sin70°
C. sin70°<cos70°<tan70°
D. cos70°<sin70°<tan70°
D
课堂练习
3.如图,在 Rt△ABC 中,∠C = 90°,AB = 10,BC = 6,求 sinA,cosA,tanA 的值.
解:由勾股定理得
10
6
4.如图,在 Rt△ABC中,∠C = 90°,BC = 6,sinA = ,求 cosA,tanB 的值.
课堂练习
A
B
C
6
解:在 Rt△ABC 中,
课堂练习
A
B
C
5.如图,在 Rt△ABC 中,∠C = 90°, ,BC = 3,求 sinB 及 Rt△ABC 的面积.
解:∵∠C = 90°, ∴
∴ AB = 3BC = 3×3 = 9.
课堂总结
本节课你学到了什么?
1.在Rt△ABC中,设∠C=90°,∠α为Rt△ABC的一个锐角,则
2.一般的,在Rt△ABC中,当∠C=90°时,
sin A=cos B,cos A=sin B,tan A · tan B=1.
板书设计
课题:1.1 锐角三角函数(1)
教师板演区
学生展示区
一、三角函数
二、正弦
三、余弦
四、正切
作业布置
课本 P6 练习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.1 锐角三角函数(1)
浙教版九年级下册
教学目标
1.理解锐角三角函数的概念,并能将三角函数表示为两条线段的比;
2.了解直角三角形中的两个锐角三角函数值之间的关系;
3.了解直角三角形中的边与三角函数值的关系。
教学重难点
重点:
理解锐角三角函数的概念,并能将三角函数表示为两条线段的比。
难点:
直角三角形中锐角三角函数值与三边之间的关系及求三角函数值。
新知导入
两个物体在倾斜角不同的斜面上向上运动相同的距离,它们上升的高度相同吗?
新知导入
从下图我们可以看到,在倾斜角(∠α ,∠ β)不同的两个斜面上,物体前进的距离都是l,而它在水平和铅垂两个方向上运动的距离却各不相同。物体在斜面上运动时,在斜面上所经过的距离和水平方向、铅垂方向经过的距离,与斜面的倾斜角之间有什么关系呢?
新知讲解
小组合作
1.作一个30°的∠A,在角的边上任意取一点B,作BC⊥AC于点C.
计算 的值,并将所得的结果与你的同伴所得的结果作比较.
新知讲解
小组合作
2.作一个50°的∠A,在角的边上任意取一点B,作BC⊥AC于点C.
量出AB,AC,BC的长(精确到1mm),计算 的值,并将所得的结果与你的同伴所得的结果作比较.
通过上面两个实践操作,你发现了什么?
新知讲解
3.如图,B,B1是∠α一边上的任意两点,作BC⊥AC与点C,B1C1⊥AC1于点C1.
判断比值
是否相等,并说明理由。
新知讲解
一般地,对于每一个确定的锐角α,在角的一边上任取一点B,作BC⊥AC于点C,比值 都是一个确定的值,与点B在角的边上的位置无关。
【总结归纳】
新知讲解
而当锐角α变化时,比值 都发生了变化,因此,我们把比值 看做是关于锐角α的函数。
比值 叫做∠α的正弦,记作sinα,即sin α=
新知讲解
比值 叫做∠α的余弦,记作cosα,即cos α=
比值 叫做∠α的正切,记作tanα,即tan α=
注意:sinα,cosα,tanα都是一个完整的符号,单独的“sin”没有意义。
其中α前面的“∠"一般省略不写.
新知讲解
锐角α的正弦、余弦和正切统称∠α的三角函数。
如果∠ A是Rt△的一个锐角,则有
新知讲解
师:根据上面的三角函数定义,你知道正弦与余弦三角函数值的取值范围吗?
∴ 0
新知讲解
【例1】如图,在Rt△ABC中,∠C=Rt∠,AB=5,BC=3.
求∠A的正弦、余弦和正切.
解:如图,在Rt△ABC中,AB=5,BC=3,
新知讲解
【拓展延伸】如图,在Rt△ABC中,∠C=Rt∠,AB=5,BC=3.
你能求出∠B的正弦、余弦和正切吗?
解:如图,在Rt△ABC中,AB=5,BC=3,
新知讲解
【思考】观察以上的计算结果,你发现了什么?
总结:
在同一个直角三角形中,sin A=cos B.
cos A=sin B,
tan A · tan B=1.
课堂练习
1. 在△ABC中,∠C = 90°,AB = 7,BC = 3,则 sinA 的值为 ( )
A. B.
C. D.
C
课堂练习
2. sin70°,cos70°,tan70° 的大小关系是 ( )
A. tan70°<cos70°<sin70°
B. cos70°<tan70°<sin70°
C. sin70°<cos70°<tan70°
D. cos70°<sin70°<tan70°
D
课堂练习
3.如图,在 Rt△ABC 中,∠C = 90°,AB = 10,BC = 6,求 sinA,cosA,tanA 的值.
解:由勾股定理得
10
6
4.如图,在 Rt△ABC中,∠C = 90°,BC = 6,sinA = ,求 cosA,tanB 的值.
课堂练习
A
B
C
6
解:在 Rt△ABC 中,
课堂练习
A
B
C
5.如图,在 Rt△ABC 中,∠C = 90°, ,BC = 3,求 sinB 及 Rt△ABC 的面积.
解:∵∠C = 90°, ∴
∴ AB = 3BC = 3×3 = 9.
课堂总结
本节课你学到了什么?
1.在Rt△ABC中,设∠C=90°,∠α为Rt△ABC的一个锐角,则
2.一般的,在Rt△ABC中,当∠C=90°时,
sin A=cos B,cos A=sin B,tan A · tan B=1.
板书设计
课题:1.1 锐角三角函数(1)
教师板演区
学生展示区
一、三角函数
二、正弦
三、余弦
四、正切
作业布置
课本 P6 练习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
