【新课标】1.1 锐角三角函数(2) 课件(共29张PPT)
文档属性
| 名称 | 【新课标】1.1 锐角三角函数(2) 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-21 00:00:00 | ||
图片预览






文档简介
(共29张PPT)
1.1 锐角三角函数(2)
浙教版九年级下册
教学目标
1.能够进行30°、45°、60°角的三角函数值的计算.
2.能够根据30°、45°、60°的三角函数值说明相应的锐角的大小.
3.经历探索30°、45°、60°角的三角函数值的过程,能够进行有关的推理,进一步体会三角函数的意义.
教学重难点
重点:
1.探索 30°、45°、60°角的三角函数值.
2.能够进行含 30°、45°、60°角的三角函数值的计算.
难点:
进一步体会三角函数的意义.
新知导入
1.在Rt△ABC中,设∠C=90°,∠A为Rt△ABC的一个锐角,则
锐角三角函数
新知导入
小明为了测量学校旗杆的高度,准备了如下测量工具:
①含30°和60°两个锐角的三角尺;
②皮尺.
你能设计一个测量方案,测出学校旗杆的高度吗?
新知讲解
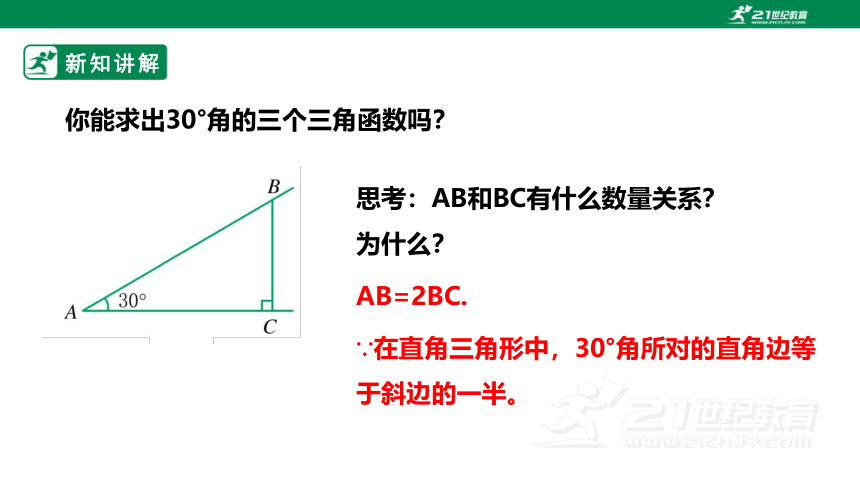
你能求出30°角的三个三角函数吗?
思考:AB和BC有什么数量关系?
为什么?
AB=2BC.
∵在直角三角形中,30°角所对的直角边等于斜边的一半。
新知讲解
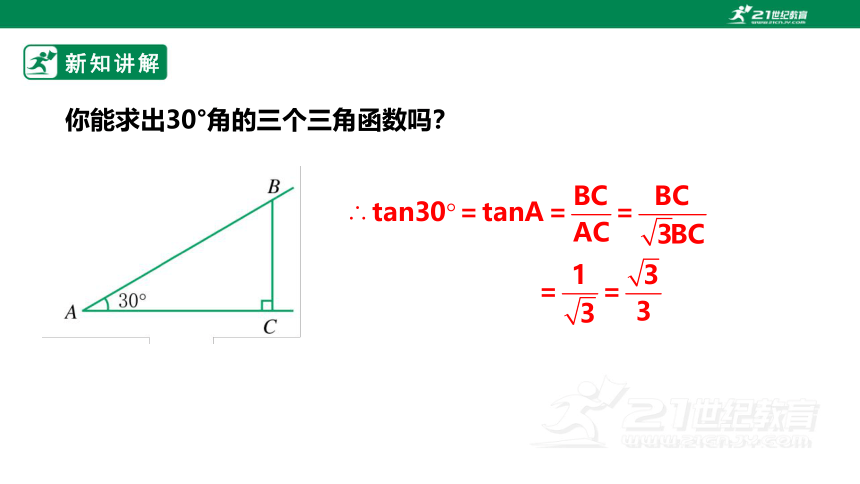
你能求出30°角的三个三角函数吗?
∴AC= =
==BC
新知讲解
你能求出30°角的三个三角函数吗?
新知讲解
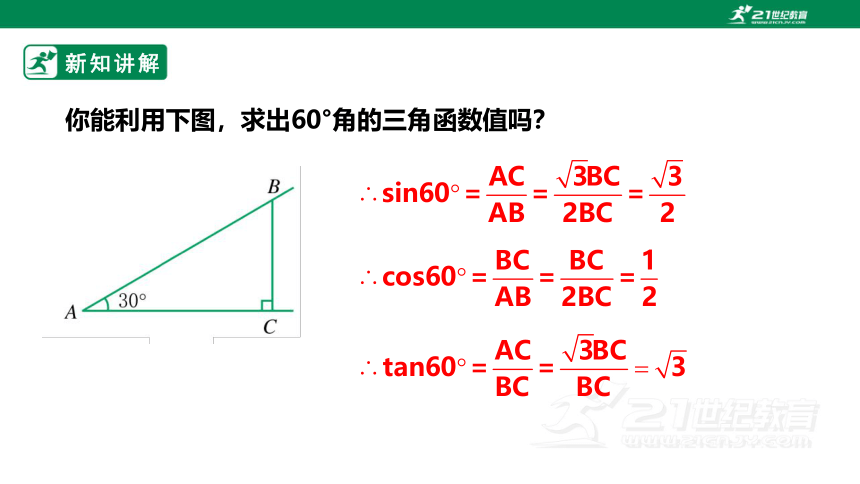
你能利用下图,求出60°角的三角函数值吗?
新知讲解
【做一做】求45°角的正弦、余弦和正切.
设其中一条直角边为a,则另一条直角边为a,斜边为
a
a
α 30° 45° 60°
sinα
cosα
tanα
新知讲解
根据上面的结果,将30°,45°,60°角的三角函数值填入下表.
1
α 30° 45° 60°
sinα
新知讲解
观察表格中函数值的特点,先看第一行30°、45°、60°角的正弦值,你能发现什么规律呢?
30°、45°、60°角的正弦值分母都为2,分子从小到大分别为 ,
,随着角度的增大,正弦值在逐渐增大.
α 30° 45° 60°
cosα
新知讲解
观察第二行30°、45°、60°角的余弦值,你能发现什么规律呢?
30°、45°、60°角的余弦值分母也都是2,而分子从小到大分别为
,余弦值随着角度的增大而减小.
α 30° 45° 60°
tanα
新知讲解
观察第三行30°、45°、60°角的正切值,你能发现什么规律呢?
1
第三行是30°、45°、60°角的正切值,首先45°角是等腰直角三角形中的一个锐角,所以tan45°=1比较特殊.
新知讲解
【例2】求下列各式的值:
(1)2sin 30°-3cos 60°.
(2)cos2 45°+tan 60°·sin 60°
cos245°表示(cos45°)2
(2)cos2 45°+tan 60°·sin 60°
新知讲解
【例2】求下列各式的值:
(3) cos 30°- sin 45°+tan 45°·cos 60°
新知讲解
【例3】如图,在△ABC中,AB=AC=8cm,∠BAC=120°.
求BC的长和△ABC的面积.
解:如图,作AD⊥BC。
在△ABC中,AB=AC,∠BAC=120°, ∴∠BAD=∠CAD= ∠BAC=60°
新知讲解
【例3】如图,在△ABC中,AB=AC=8cm,∠BAC=120°.
求BC的长和△ABC的面积.
∴BD=ABsin∠BAD=8sin60°
新知讲解
【例3】如图,在△ABC中,AB=AC=8cm,∠BAC=120°.
求BC的长和△ABC的面积.
课堂练习
C
2.周长为15 cm的等腰三角形的底边长是5 cm,则底角的余弦值为
________.
课堂练习
3.计算:
(1)2sin245°-tan 60°·cos 30°.
(2)sin 30°+cos 60°+tan 45°.
课堂练习
解:如图,过点A作AD⊥BC于点D.
D
课堂练习
D
5.已知△ABC中的∠A 与锐角∠B 满足 (1-tanA)2 +|sinB- |=0,试判断△ABC 的形状.
课堂练习
解:∵ (1-tanA)2 + | sinB- |=0,
∴ tanA=1,sinB=
∴∠A=45°,锐角∠B=60°.
∴∠C=180°-45°-60°=75°.
∴△ABC 是锐角三角形.
课堂总结
本节课你学到了什么?
探索30°、45°、60°角的三角函数值.
sin30°= sin45°= sin60°=
cos30°= cos45°= cos60°=
tan30°= tan45°= tan60°=
1
板书设计
课题:1.1 锐角三角函数(2)
教师板演区
学生展示区
一、特殊角的正弦、余弦、正切的值。
二、例题讲解
作业布置
课本 P9 练习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.1 锐角三角函数(2)
浙教版九年级下册
教学目标
1.能够进行30°、45°、60°角的三角函数值的计算.
2.能够根据30°、45°、60°的三角函数值说明相应的锐角的大小.
3.经历探索30°、45°、60°角的三角函数值的过程,能够进行有关的推理,进一步体会三角函数的意义.
教学重难点
重点:
1.探索 30°、45°、60°角的三角函数值.
2.能够进行含 30°、45°、60°角的三角函数值的计算.
难点:
进一步体会三角函数的意义.
新知导入
1.在Rt△ABC中,设∠C=90°,∠A为Rt△ABC的一个锐角,则
锐角三角函数
新知导入
小明为了测量学校旗杆的高度,准备了如下测量工具:
①含30°和60°两个锐角的三角尺;
②皮尺.
你能设计一个测量方案,测出学校旗杆的高度吗?
新知讲解
你能求出30°角的三个三角函数吗?
思考:AB和BC有什么数量关系?
为什么?
AB=2BC.
∵在直角三角形中,30°角所对的直角边等于斜边的一半。
新知讲解
你能求出30°角的三个三角函数吗?
∴AC= =
==BC
新知讲解
你能求出30°角的三个三角函数吗?
新知讲解
你能利用下图,求出60°角的三角函数值吗?
新知讲解
【做一做】求45°角的正弦、余弦和正切.
设其中一条直角边为a,则另一条直角边为a,斜边为
a
a
α 30° 45° 60°
sinα
cosα
tanα
新知讲解
根据上面的结果,将30°,45°,60°角的三角函数值填入下表.
1
α 30° 45° 60°
sinα
新知讲解
观察表格中函数值的特点,先看第一行30°、45°、60°角的正弦值,你能发现什么规律呢?
30°、45°、60°角的正弦值分母都为2,分子从小到大分别为 ,
,随着角度的增大,正弦值在逐渐增大.
α 30° 45° 60°
cosα
新知讲解
观察第二行30°、45°、60°角的余弦值,你能发现什么规律呢?
30°、45°、60°角的余弦值分母也都是2,而分子从小到大分别为
,余弦值随着角度的增大而减小.
α 30° 45° 60°
tanα
新知讲解
观察第三行30°、45°、60°角的正切值,你能发现什么规律呢?
1
第三行是30°、45°、60°角的正切值,首先45°角是等腰直角三角形中的一个锐角,所以tan45°=1比较特殊.
新知讲解
【例2】求下列各式的值:
(1)2sin 30°-3cos 60°.
(2)cos2 45°+tan 60°·sin 60°
cos245°表示(cos45°)2
(2)cos2 45°+tan 60°·sin 60°
新知讲解
【例2】求下列各式的值:
(3) cos 30°- sin 45°+tan 45°·cos 60°
新知讲解
【例3】如图,在△ABC中,AB=AC=8cm,∠BAC=120°.
求BC的长和△ABC的面积.
解:如图,作AD⊥BC。
在△ABC中,AB=AC,∠BAC=120°, ∴∠BAD=∠CAD= ∠BAC=60°
新知讲解
【例3】如图,在△ABC中,AB=AC=8cm,∠BAC=120°.
求BC的长和△ABC的面积.
∴BD=ABsin∠BAD=8sin60°
新知讲解
【例3】如图,在△ABC中,AB=AC=8cm,∠BAC=120°.
求BC的长和△ABC的面积.
课堂练习
C
2.周长为15 cm的等腰三角形的底边长是5 cm,则底角的余弦值为
________.
课堂练习
3.计算:
(1)2sin245°-tan 60°·cos 30°.
(2)sin 30°+cos 60°+tan 45°.
课堂练习
解:如图,过点A作AD⊥BC于点D.
D
课堂练习
D
5.已知△ABC中的∠A 与锐角∠B 满足 (1-tanA)2 +|sinB- |=0,试判断△ABC 的形状.
课堂练习
解:∵ (1-tanA)2 + | sinB- |=0,
∴ tanA=1,sinB=
∴∠A=45°,锐角∠B=60°.
∴∠C=180°-45°-60°=75°.
∴△ABC 是锐角三角形.
课堂总结
本节课你学到了什么?
探索30°、45°、60°角的三角函数值.
sin30°= sin45°= sin60°=
cos30°= cos45°= cos60°=
tan30°= tan45°= tan60°=
1
板书设计
课题:1.1 锐角三角函数(2)
教师板演区
学生展示区
一、特殊角的正弦、余弦、正切的值。
二、例题讲解
作业布置
课本 P9 练习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
