浙教版八年级上册 2.1 图形的轴对称 课件(共22张PPT)
文档属性
| 名称 | 浙教版八年级上册 2.1 图形的轴对称 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 13.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-24 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
古从军行
〔唐〕李颀
白日登山望烽火,将军饮马傍交河。
……
2.1图形的轴对称
观察这些图有什么特点?
沿着一条直线折叠后,直线两侧的部分能够相互重合
回顾旧知
回顾旧知
对称轴:这条直线叫做对称轴
轴对称图形:把一个图形沿着一条直线折叠后,直线两侧的部分能够相互重合,那么这个图形叫做轴对称图形。
2条对称轴
4条对称轴
无数条对称轴
线段是轴对称图形,它的对称轴是这条线段的垂直平分线
角是轴对称图形,它的对称轴是这个角的平分线所在的直线。
A
B
E
F
轴对称图形沿对称轴对折后互相重合的两个点叫做对称点
如图:点A的对称点是点B
O
完成合作学习单中的第1题(1)(2)
对称轴垂直平分连结两个对称点的线段
轴对称图形的性质:
完成合作学习单中的第1题
尝试完成导学案中的第2题,并小组讨论。
讲授新知
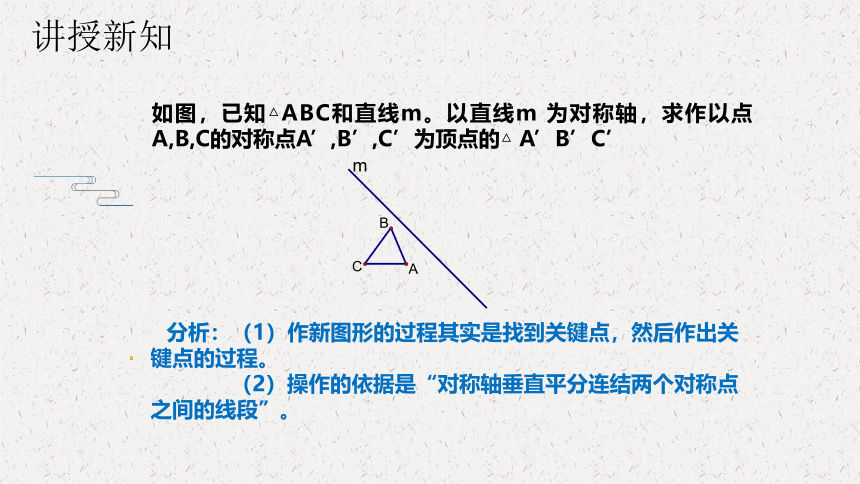
如图,已知△ABC和直线m。以直线m 为对称轴,求作以点A,B,C的对称点A’,B’,C’为顶点的△ A’B’C’
m
B
C
A
分析:(1)作新图形的过程其实是找到关键点,然后作出关 键点的过程。
(2)操作的依据是“对称轴垂直平分连结两个对称点之间的线段”。
例题讲解
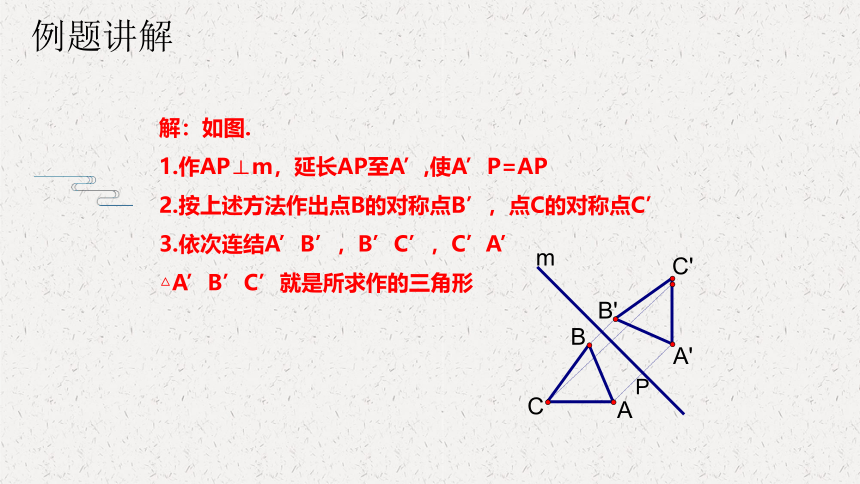
解:如图.
1.作AP⊥m,延长AP至A’,使A’P=AP
2.按上述方法作出点B的对称点B’,点C的对称点C’
3.依次连结A’B’,B’C’,C’A’
△A’B’C’就是所求作的三角形
m
A'
C'
B'
B
C
A
P
如果把右图沿直线m 折叠,两个三角形会重合吗?如果重合,这说明什么?
能重合,说明
(1)轴对称变换不改变原图形的形状和大小。
(2)经轴对称变换所得的图形和原图形全等。
由一个图形变为另一个图形,并使这两个图形沿某一条直线折叠后能够互相重合,这样的图形改变叫做图形的轴对称。这条直线叫做对称轴
图形的轴对称有下面的性质:
成轴对称的两个图形是全等图形
思考探究
古从军行
〔唐〕李颀
白日登山望烽火,将军饮马傍交河。
……
B
A
l
一位将军从图中的A 地出发,到一条笔直的河边l 饮马,然后回到B 地军营.请问到河边什么地方饮马可使他所走的路径最短?
将军饮马问题
探索新知
B
·
·
A
l
C
将军饮马问题
两点之间
线段最短
C
探究1 若A、B两地如图所示,请问到河边什么地方饮马可使将军所走的路径最短?
●
探索新知
作图问题:请在直线 上找到一点C,使得AC+BC最短。
B
·
·
A
l
C
探究2 若A,B 两地如图所示,又如何在河l上找到饮马点C,使得AC+BC最短?
将军饮马问题
探索新知
思考:
能把A、B 两点转化到直线l 的两侧吗?
B
·
l
A
·
C
将军饮马问题
B
·
·
A
l
C
探索新知
方法揭晓
作法:
(1)作点B 关于直线l 的对称点B′;
(2)连接AB′,与直线l 相交于点C.
则点C 即为所求.
A
B
l
B′
C
此时路径A-C-B是最短路径。
将军饮马问题
A′
将军饮马问题
B
·
l
A
·
C
作点A或点B关于直线l的对称点,所得到的C点位置不变
方法提示
B
·
l
A
·
C
B′
你能用所学的知识证明AC +BC最短吗?
由轴对称的性质可知,BC =B′C ,BC′=B′C′.
在△AB′C′中,
∵ AB′<AC′+B′C′,
∴ AC +BC<AC′+BC′.
即 AC +BC 最短.
A
B
l
B′
C
C ′
证明:如图,在直线l 上任取一点C′(与点C 不重合),连接AC′,BC′,B′C′.
∴AC +BC= AC +B′C = AB′
∴ AC′+BC′= AC′+ B′C′
理论证明
2.最短距离问题的解决方法:
1.基本模型:
l
A
B
A′
C
当两定点在直线同侧时
C
A
l
B
当两定点在直线异侧时
利用“轴对称”
化折为直
阶段小结
“转化”的思想
探究3 若将军要先让马到草地OM吃草,再到河边ON喝水,最后回到出发点A,你能画出最短路径吗?
M
将军饮马问题
N
O
草地
河流
A
课后思考
轴对称图形的定义
轴对称图形的性质
图形轴对称性质
“转化”思想
课后总结
感
谢
观
看
Exquisite Office PowerPoint templates come from MC design
古从军行
〔唐〕李颀
白日登山望烽火,将军饮马傍交河。
……
2.1图形的轴对称
观察这些图有什么特点?
沿着一条直线折叠后,直线两侧的部分能够相互重合
回顾旧知
回顾旧知
对称轴:这条直线叫做对称轴
轴对称图形:把一个图形沿着一条直线折叠后,直线两侧的部分能够相互重合,那么这个图形叫做轴对称图形。
2条对称轴
4条对称轴
无数条对称轴
线段是轴对称图形,它的对称轴是这条线段的垂直平分线
角是轴对称图形,它的对称轴是这个角的平分线所在的直线。
A
B
E
F
轴对称图形沿对称轴对折后互相重合的两个点叫做对称点
如图:点A的对称点是点B
O
完成合作学习单中的第1题(1)(2)
对称轴垂直平分连结两个对称点的线段
轴对称图形的性质:
完成合作学习单中的第1题
尝试完成导学案中的第2题,并小组讨论。
讲授新知
如图,已知△ABC和直线m。以直线m 为对称轴,求作以点A,B,C的对称点A’,B’,C’为顶点的△ A’B’C’
m
B
C
A
分析:(1)作新图形的过程其实是找到关键点,然后作出关 键点的过程。
(2)操作的依据是“对称轴垂直平分连结两个对称点之间的线段”。
例题讲解
解:如图.
1.作AP⊥m,延长AP至A’,使A’P=AP
2.按上述方法作出点B的对称点B’,点C的对称点C’
3.依次连结A’B’,B’C’,C’A’
△A’B’C’就是所求作的三角形
m
A'
C'
B'
B
C
A
P
如果把右图沿直线m 折叠,两个三角形会重合吗?如果重合,这说明什么?
能重合,说明
(1)轴对称变换不改变原图形的形状和大小。
(2)经轴对称变换所得的图形和原图形全等。
由一个图形变为另一个图形,并使这两个图形沿某一条直线折叠后能够互相重合,这样的图形改变叫做图形的轴对称。这条直线叫做对称轴
图形的轴对称有下面的性质:
成轴对称的两个图形是全等图形
思考探究
古从军行
〔唐〕李颀
白日登山望烽火,将军饮马傍交河。
……
B
A
l
一位将军从图中的A 地出发,到一条笔直的河边l 饮马,然后回到B 地军营.请问到河边什么地方饮马可使他所走的路径最短?
将军饮马问题
探索新知
B
·
·
A
l
C
将军饮马问题
两点之间
线段最短
C
探究1 若A、B两地如图所示,请问到河边什么地方饮马可使将军所走的路径最短?
●
探索新知
作图问题:请在直线 上找到一点C,使得AC+BC最短。
B
·
·
A
l
C
探究2 若A,B 两地如图所示,又如何在河l上找到饮马点C,使得AC+BC最短?
将军饮马问题
探索新知
思考:
能把A、B 两点转化到直线l 的两侧吗?
B
·
l
A
·
C
将军饮马问题
B
·
·
A
l
C
探索新知
方法揭晓
作法:
(1)作点B 关于直线l 的对称点B′;
(2)连接AB′,与直线l 相交于点C.
则点C 即为所求.
A
B
l
B′
C
此时路径A-C-B是最短路径。
将军饮马问题
A′
将军饮马问题
B
·
l
A
·
C
作点A或点B关于直线l的对称点,所得到的C点位置不变
方法提示
B
·
l
A
·
C
B′
你能用所学的知识证明AC +BC最短吗?
由轴对称的性质可知,BC =B′C ,BC′=B′C′.
在△AB′C′中,
∵ AB′<AC′+B′C′,
∴ AC +BC<AC′+BC′.
即 AC +BC 最短.
A
B
l
B′
C
C ′
证明:如图,在直线l 上任取一点C′(与点C 不重合),连接AC′,BC′,B′C′.
∴AC +BC= AC +B′C = AB′
∴ AC′+BC′= AC′+ B′C′
理论证明
2.最短距离问题的解决方法:
1.基本模型:
l
A
B
A′
C
当两定点在直线同侧时
C
A
l
B
当两定点在直线异侧时
利用“轴对称”
化折为直
阶段小结
“转化”的思想
探究3 若将军要先让马到草地OM吃草,再到河边ON喝水,最后回到出发点A,你能画出最短路径吗?
M
将军饮马问题
N
O
草地
河流
A
课后思考
轴对称图形的定义
轴对称图形的性质
图形轴对称性质
“转化”思想
课后总结
感
谢
观
看
Exquisite Office PowerPoint templates come from MC design
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
