浙教版九年级上册 第三章 圆的基本性质 复习课件(共16张PPT)
文档属性
| 名称 | 浙教版九年级上册 第三章 圆的基本性质 复习课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-24 00:00:00 | ||
图片预览

文档简介
(共16张PPT)
圆的基本性质复习
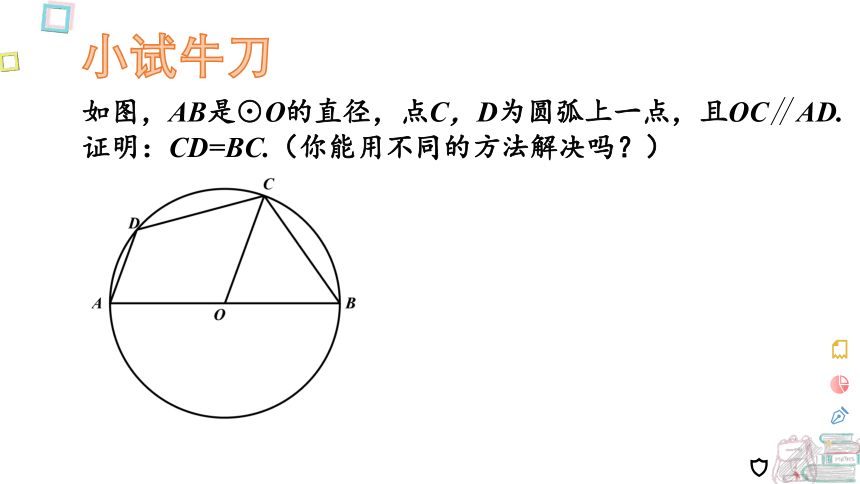
如图,AB是⊙O的直径,点C,D为圆弧上一点,且OC∥AD.
证明:CD=BC.(你能用不同的方法解决吗?)
小试牛刀
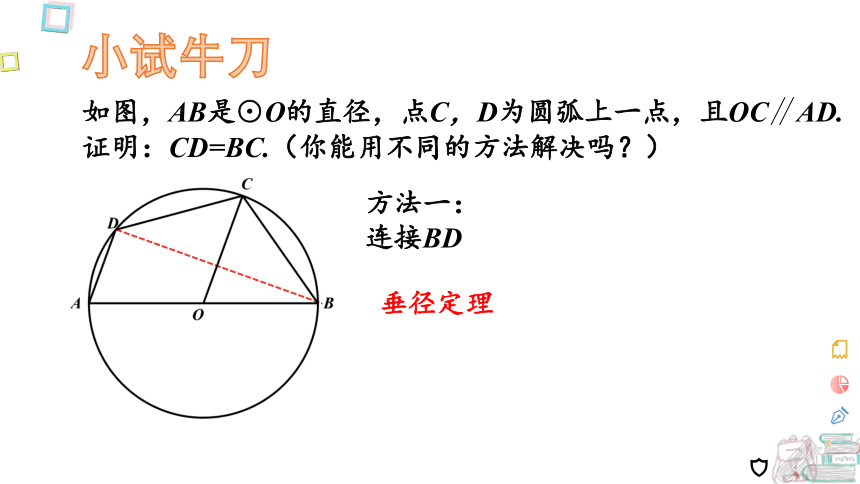
方法一:
连接BD
垂径定理
如图,AB是⊙O的直径,点C,D为圆弧上一点,且OC∥AD.
证明:CD=BC.(你能用不同的方法解决吗?)
小试牛刀
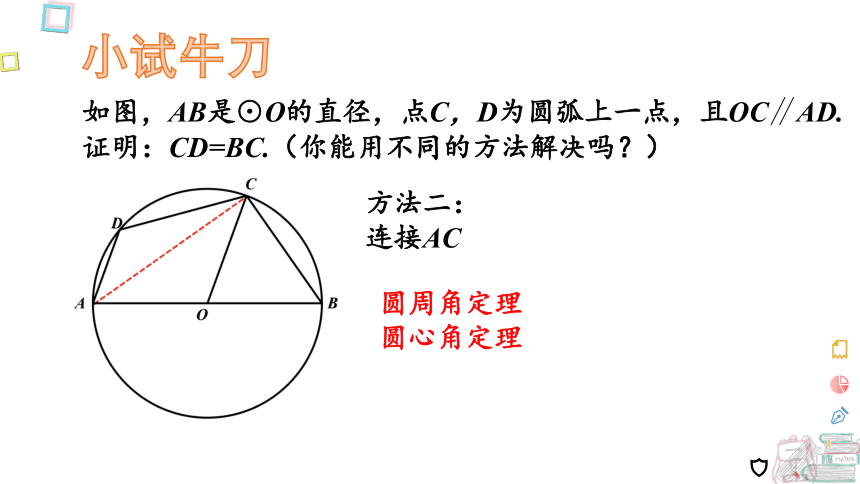
方法二:
连接AC
圆周角定理
圆心角定理
如图,AB是⊙O的直径,点C,D为圆弧上一点,且OC∥AD.
证明:CD=BC.(你能用不同的方法解决吗?)
小试牛刀
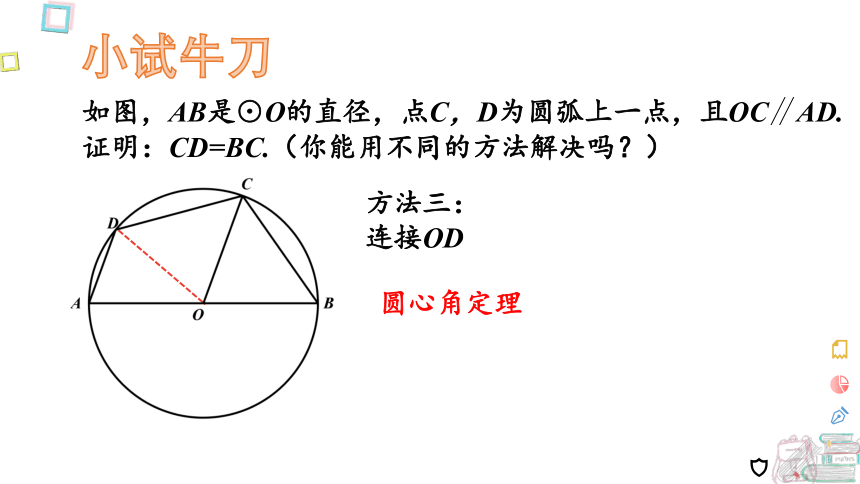
方法三:
连接OD
圆心角定理
如图,AB是⊙O的直径,点C,D为圆弧上一点,且OC∥AD.
证明:CD=BC.(你能用不同的方法解决吗?)
小试牛刀
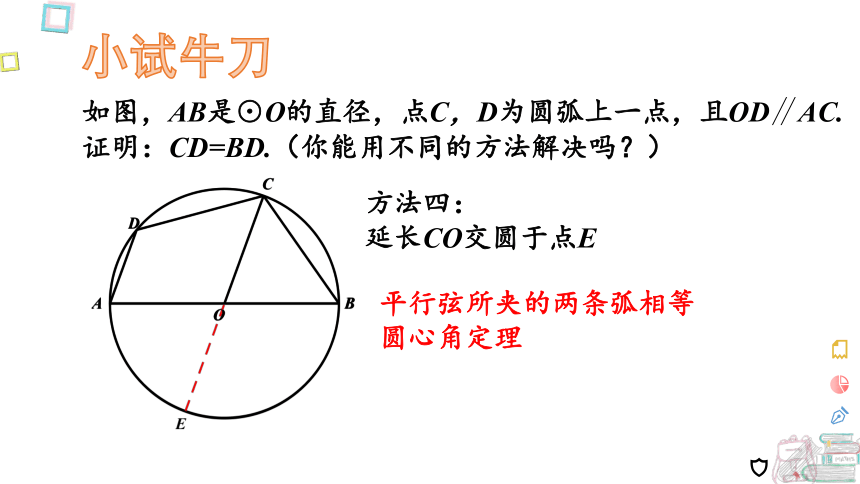
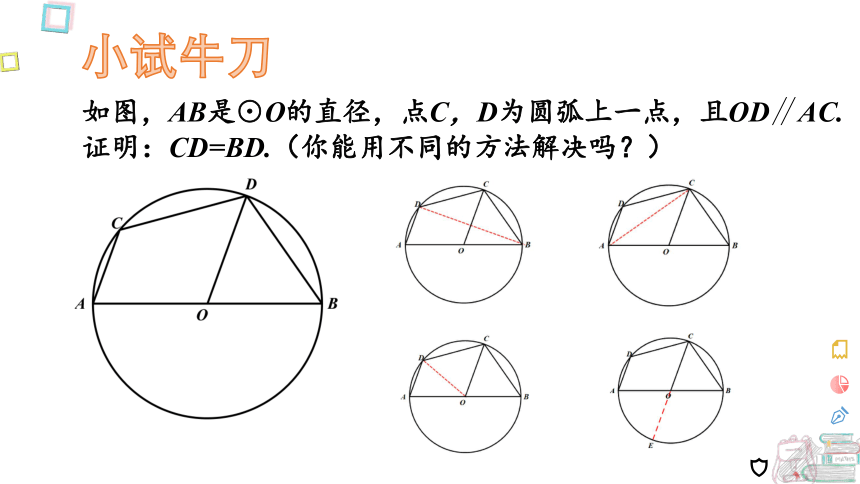
如图,AB是⊙O的直径,点C,D为圆弧上一点,且OD∥AC.
证明:CD=BD.(你能用不同的方法解决吗?)
方法四:
延长CO交圆于点E
平行弦所夹的两条弧相等
圆心角定理
小试牛刀
如图,AB是⊙O的直径,点C,D为圆弧上一点,且OD∥AC.
证明:CD=BD.(你能用不同的方法解决吗?)
小试牛刀
圆心角相等
弦相等
圆周角相等
弧相等
弦心距相等
直径平分弦
直径垂直弦
直径平分弧
(弦不是直径)
旋转不变性
轴对称性
圆的基本性质
经验总结
如图,AB是⊙O的直径,点C、点D为同侧圆上两点,AD∥OC,连接AC,CD,CB.
除了相等的弧、角、线段之外,还有哪些特殊的角?特殊的图形?
弧:
线段:
角:
∠CAD=∠CAB=∠ACO
CD=BC
CD=BC(弦)
OA=OB=OC(半径)
(
(
∠ACD=90°
∠B+∠D=180°
如图,AB是⊙O的直径,点C、点D为同侧圆上两点,AD∥OC,连接AC,CD.若AD=6 , AB=10
你能求出哪些线段的长度?
垂径定理
连接BD
Rt△CBE
Rt△OBE
勾股定理
构造
如图,AB是⊙O的直径,点C、点D为同侧圆上两点,AD∥OC,连接AC,CD.若AD=6, AB=10
你能求出哪些线段的长度?
圆心角定理
连接BC
Rt△CBA
勾股定理
构造
如图,AB是⊙O的直径,点C、点D为同侧圆上两点,AD∥OC,连接AC,CD.若AD=6,AB=10
你能求出哪些线段的长度?
连接BD
连接BC
构造
相似三角形性质
如图,AB是⊙O的直径,点C、点D为同侧圆上两点,AD∥OC,连接AC,CD.若AD= 6,AB=10
你能求出哪些线段的长度?
连接BC并延长交AD延长线于点P
构造
相似三角形性质
如图,AB是⊙O的直径,点C、点D为同侧圆上两点,AD∥OC,连接AC,CD.若AO=4,CD=x,AD=y
(1)求y关于x的关系式;
(2)求四边形AOCD周长的最大值.
几何最值问题
函数最值
函数模型
谈谈收获
圆的基本性质
轴对称性
旋转不变性
垂径定理
圆心角定理
找等量
构造(找)特殊图形
直角三角形
勾股定理
相似三角形
相似的性质
几何问题
函数问题
函数模型
线段间
数量关系
谢谢聆听
圆的基本性质复习
如图,AB是⊙O的直径,点C,D为圆弧上一点,且OC∥AD.
证明:CD=BC.(你能用不同的方法解决吗?)
小试牛刀
方法一:
连接BD
垂径定理
如图,AB是⊙O的直径,点C,D为圆弧上一点,且OC∥AD.
证明:CD=BC.(你能用不同的方法解决吗?)
小试牛刀
方法二:
连接AC
圆周角定理
圆心角定理
如图,AB是⊙O的直径,点C,D为圆弧上一点,且OC∥AD.
证明:CD=BC.(你能用不同的方法解决吗?)
小试牛刀
方法三:
连接OD
圆心角定理
如图,AB是⊙O的直径,点C,D为圆弧上一点,且OC∥AD.
证明:CD=BC.(你能用不同的方法解决吗?)
小试牛刀
如图,AB是⊙O的直径,点C,D为圆弧上一点,且OD∥AC.
证明:CD=BD.(你能用不同的方法解决吗?)
方法四:
延长CO交圆于点E
平行弦所夹的两条弧相等
圆心角定理
小试牛刀
如图,AB是⊙O的直径,点C,D为圆弧上一点,且OD∥AC.
证明:CD=BD.(你能用不同的方法解决吗?)
小试牛刀
圆心角相等
弦相等
圆周角相等
弧相等
弦心距相等
直径平分弦
直径垂直弦
直径平分弧
(弦不是直径)
旋转不变性
轴对称性
圆的基本性质
经验总结
如图,AB是⊙O的直径,点C、点D为同侧圆上两点,AD∥OC,连接AC,CD,CB.
除了相等的弧、角、线段之外,还有哪些特殊的角?特殊的图形?
弧:
线段:
角:
∠CAD=∠CAB=∠ACO
CD=BC
CD=BC(弦)
OA=OB=OC(半径)
(
(
∠ACD=90°
∠B+∠D=180°
如图,AB是⊙O的直径,点C、点D为同侧圆上两点,AD∥OC,连接AC,CD.若AD=6 , AB=10
你能求出哪些线段的长度?
垂径定理
连接BD
Rt△CBE
Rt△OBE
勾股定理
构造
如图,AB是⊙O的直径,点C、点D为同侧圆上两点,AD∥OC,连接AC,CD.若AD=6, AB=10
你能求出哪些线段的长度?
圆心角定理
连接BC
Rt△CBA
勾股定理
构造
如图,AB是⊙O的直径,点C、点D为同侧圆上两点,AD∥OC,连接AC,CD.若AD=6,AB=10
你能求出哪些线段的长度?
连接BD
连接BC
构造
相似三角形性质
如图,AB是⊙O的直径,点C、点D为同侧圆上两点,AD∥OC,连接AC,CD.若AD= 6,AB=10
你能求出哪些线段的长度?
连接BC并延长交AD延长线于点P
构造
相似三角形性质
如图,AB是⊙O的直径,点C、点D为同侧圆上两点,AD∥OC,连接AC,CD.若AO=4,CD=x,AD=y
(1)求y关于x的关系式;
(2)求四边形AOCD周长的最大值.
几何最值问题
函数最值
函数模型
谈谈收获
圆的基本性质
轴对称性
旋转不变性
垂径定理
圆心角定理
找等量
构造(找)特殊图形
直角三角形
勾股定理
相似三角形
相似的性质
几何问题
函数问题
函数模型
线段间
数量关系
谢谢聆听
同课章节目录
