第四章复习[上学期]

课件25张PPT。第四章 复习课书写格式：（1）1乘以a写成————a（2）－1乘以a写成————－a（3）a÷5一般写成————（5）数字与数字相乘时，乘号不能省略31、判断下列式子是否为代数式，并说明理由。
(1)2x-y (2)a+b=c (3)x>4
(4)-1 (5)V=abc (6)
2、说明下列各代数式书写的是否合理，并简要说明理由。
3)3(y代数式3.用代数式表示①5除a的商④n的倒数与-2的差⑤a与b的和的立方⑥a与b两数的立方和⑦a与b的立方的和(a+b)3a3 +b3a+b34.下列代数式表达合理吗?二.代数式的值解:注意:②字母取负值或分数时要添括号①书写格式 当….时4.挑战题3.试一试:由数与字母或字母与字母相乘组成的代数式叫做单项式。
单独一个数或一个字母也叫做单项式，如 0，-1，a,-2b.单项式中的数字因数叫做这个单项式的系数；一个单项式中，所有字母的指数的和叫做这个单项式的次数。练习：1.-3x的次数是 ，ab的次数是 。
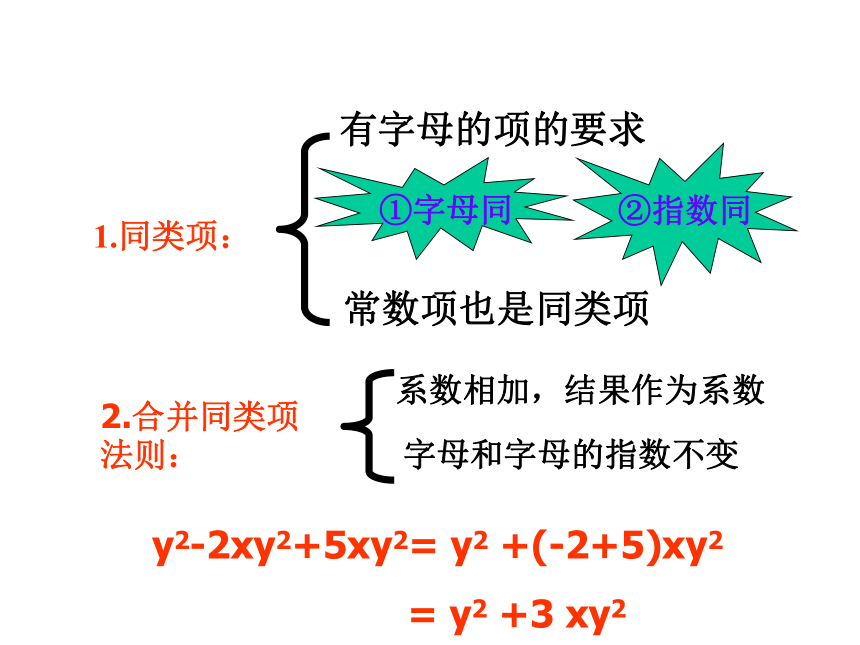
2.2?r的数字因数是 ，所以2?r的系数是 ；3. 4x2yz的次数是 ，它是 次单项式。单项式多项式 由几个单项式相加减组成的代数式叫做多项式。 在多项式中，每个单项式叫做多项式的项，不含字母的项叫做常数项，次数最高的项的次数就是这个多项式的次数。a2-3a-2的项有a2,-3a, 2,常数项是-2，a2-3a-2称为二次多项式.次数高的项a2的次数是2 1.同类项： 有字母的项的要求 常数项也是同类项 ①字母同②指数同2.合并同类项 法则：系数相加，结果作为系数字母和字母的指数不变 y2-2xy2+5xy2= y2 +(-2+5)xy2
= y2 +3 xy2+ (a － b + c) = ____________x－2(a － b + c) = ____________去括号法则a-b+cx-2a+2b-2c括号前面是“+”号，去掉括号和它前面的“+”号，括号里面各项都不变；括号前面是“－”号，去掉括号和它前面的“－”号，括号里的各项都变号。－ (a － b + c) = ____________-a+b-c 整式的加减总结 去括号 合并同类项1.如图，在一块长为a，宽为b，的场地内建一个球场，两边各缩进2.5米进行绿化，试用两种不同方法计算出绿化带的面积。练一练2.某校举办了一次围棋单循环比赛,即每一位选手都和其余选手比赛一局.
(1)设参加比赛的人数为n人,请n用的代数式表示这次比赛总局数;
(2)若n=5,求第(1)题所列代数式的值,并说明这个值的实际意义;
(3)若某选手中途退出了比赛,结果比赛只进行了25局,问有多少人参加比赛?中途退出的这名选手放弃了几局比赛?3.先化简,再求值:

其中4.如图，用长为22米的铝合金，做成一个长方形的窗框（中间有横档），设窗框的横条长度为x米.
（1）用代数式表示窗框的面积.
（2）若x分别取1，2，3时，哪一种取法所做的窗框的面积最大？5.一座楼梯的侧面示意图如图所示。要在楼梯上铺一条地毯，则地毯至少需多少长？若楼梯的宽为b，则地毯的面积为多少？2.现有甲种糖果a千克，售价每千克m 元；乙种糖果b千克，售价每千克n 元；若将两种糖果混在一起出售，则售价应为每千克 元。1.设奶粉每听p元，橘子每听q元，则买8听奶粉、4听橘子共需 元。(8p+4q)3.某出租车收费标准为：起步价10元，3千米到5千米每千米为1.8元， 5千米后每千米为2.7元，则某人乘坐出租车x千米（x＞5的整数）时付费为 元。（2.7x+0.1)4.一年定期的储蓄存款a元，年利率是2.25%，则一年后可取得本金利息共多少元？若存入2000元呢？5.据统计，我国从1990～2000年人均日用水量增加了40%。专家预测，2010年人均日用水量将比2000年增加 ，设1990年的人均日用水量为q，升，
（1）2010年比1990年人均日用水量增加多少升？增长的百分比是多少？
（2）已知1990年人均日用水量是25升，按所给的预测，2010年我国的人均日用水量为多少？1.张军有一部手机和一只小灵通，4月份张军在缴纳话费时发现，手机的费用是小灵通费用的1.8倍；为了控制、减少话费支出，张军决定采取一定措施，预计5月份手机的费用减少40％，小灵通的费用增加30％，你觉得张军的措施可行吗？请说明理由。想一想1.8a(1+30%)a1.8(1-40%)a2.8a2.38a根据题意填入下表2.观察下面由火柴棒拼成的一列图形，第n个图形由n 个正方形组成。
（1）第五个图形由多少根火柴组成？（2）用含n的代数式表示第n个图形所含的火柴棒根数.
（3）根据（2）的结果，写出第30个图形中的火柴棒根数.…3.如图有3个面积都是m的圆放在桌面上，桌面被圆覆盖的面积是2m+2 ，且重叠的两块图形面积相等，求重叠的每一块图形的面积。 代数式a(1+x%)可以表示什么？
试举一个实际例子，
并说明当a=3600,x=－10时
代数式的值的具体意义。探究活动 2.小明和小亮玩猜数游戏，小明说：“你随便选定三个一位数，按这样的步骤计算：⑴把第一个数乘以2；⑵加上5；⑶乘以5；⑷加上第二个数；⑸乘以10；⑹加上第三个数，只要你告诉我最后得数，我就知道你所选的三个一位数，”小亮不相信，但试了几次，小明都猜对了，你知道小明试怎样猜对的吗?探究活动