第四章复习 浙江版[上学期]

课件26张PPT。第四章 代数式
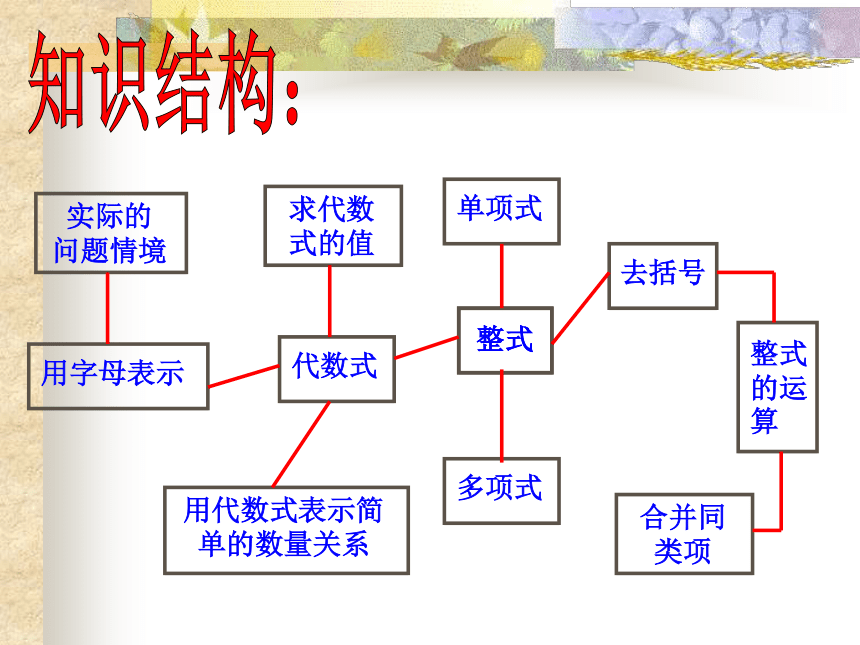
复习知识结构：1、一个代数式一般由数、表示数的字母
和运算符号组成，这里的运算是指：
、 、 、
、 、 。 单独
的一个数或者一个字母也称代数 式。知识要点：用数代替代数式里的字母，计算后所得的
结果叫做 。加法减法乘法除法乘方开方代数式的值 2、由数与字母或字母与字母相乘组成的代
式叫做 ；单项式中数字因数叫
做这个单项式的 ；所有字母的
指数的和叫做这个单项式的 。 由几个 相加组成的代数式叫做
多项式。在多项式中，每个单项式叫做多项
式的 ；不含字母的项叫做 ；
就是这个多项式的次
数。单项式系数次数单项式项常数项次数最高的项的次数单项式、多项式统称为 。整式 3、多项式中，所含 相同，并且
也相同的项，叫做
同类项。4、主要运算法则：（1）合并同类项法则：把同类项的 相
加，所得的结果作为系数，
不变。（2）去括号法则：括号前面是 “ + ” 号，
把 去掉，括
号里各项 ；字母相同字母的指数系数字母和字母的指数括号和它前面的“+”号都不变号（3）整式的加减运算可归结为 和
。（2）去括号法则：括号前面是 “ - ” 号，
把 去掉，括
号里各项 。去括号的
法则的依据是分配律，即：
a ( b + c ) = 。括号和它前面的“ – ”号都改变符号ab + ac去括号合并同类项5、主要方法和技能：（1）用代数式表示实际生活中的量，求代数式的值；
（2）整式的加减，并解决简单实际问题。书写代数式时应注意的事项:2、数字与字母相乘时数字因数写在前面，并写成省略乘号的形式;
1、字母与字母相乘时应写成省略乘号的形式;3、当数字因数是带分数时应化成假分数;4、当系数是1或-1时的1应省略不写;5、表示两者相除时应把除号写成分数线;6、后接单位的相加式子要用括号括起来，比如（2a+3b)元。
1.下列哪些属于代数式？(1) X2_ 2(2) 4r2(3) 1 (4) S=2ab（5）(7) a2(6) a×b（8）
(9) -1x(10) a÷b例题分析：2、用代数式表示：（2）某产品的价格是 p 元，其中成本比
其价格少10%，则此产品的成本是
。（1）比 a 的5倍小 3 的数是 。（3）一本书有 m 页，第一天读了全书页数
的 四分之一，第二天读了剩下的三分
之一，则没有读的页数是 。5a - 30.9p m1) x的3倍与y的差2) v1 与 v2 的和除S所得的商7)杭州湾跨海大桥的桥墩是直径为d，高为h的圆柱体，求每个桥墩的体积3) x的平方与1的和的平方根3.用代数式表示下列各题：4)a与b的平方和5) a与b 的和的平方6) a的相反数的倒数8) 稻谷加工成大米后质量一般减少２５％， （１）x千克稻谷可加工成大米多少千克？
（２）要得到y千克大米需要稻谷多少千克？ 　 　
　　则输入x×３（　　　）－１（　　　　　）÷２输出（　　　　）3x3x-14.如图是一个数值转换机示意图，请按要求在括号内填写转换步骤，在表格中填写数值。-25.仔细观察下列图形，当梯形的个数是n时，图形的周长是_________； 6.某校男生人数是女生人数的4倍，女
生人数是教师人数的9倍，设分别用
a、b、c 依次表示男生、女生及教师
人数。
（1）试用含 c 的代数式表示全校师生
的总数。
（2）若 b = 360 ，求该校师生总人数。女生人数为：9c 男生人数为：36c 全校师生总人数为 ：36c + 9c + c = 46c 当 b=360时 c = 40 ，所以 46c = 1840 （人）7.有理数 a、b、c 在数轴上的位置如图所示：试化简：解：由数轴上点的位置可知：
a + c < 0，a + b + c < 0，a – b > 0原式= - ( a +c )+( a+b+c) – ( a – b ) – ( 2b – a ) = - a – c +a+b+c – a +b – 2b +a= 08.已知一个多项式加上 5x2 + 3x – 2 的2倍得
1 – 3x2 + x ，求这个多项式。 解：这个多项式=
（1 – 3x2 + x ）- 2（5x2 + 3x – 2 ）= 1 – 3x2 + x - 10x2 - 6x + 4 = 5 – 13x2 -5x9.已知a=-5，求代数式1-(3a+1)+a2的值。10.已知代数式 ( 3a2 – ab+2b2 ) – ( a2 – 5ab+b2)
– 2 ( a2 + 2ab +b2 )。 （1）试说明这个代数式的值与 a 的取值
无关； （2）若 b = - 2 ，求这个代数式的值。解：( 1 ) 原式= 3a2 – ab+2b2 –a2 + 5ab -b2
– 2a2 - 4ab - 2b2= – b2 所以，代数式的值与a 的值无关。（2）当 b = - 2 时，原式 = - (-2)2 = - 4 。1、当 m = 时，代数式 3xmy与 –2x2 y
是同类项。2、若 a – b =10，那么15 – a + b 的值是 。3、若 A – (- 3x ) = x2 + 3x – 1 ，则 A= 。2515 – a + b = 10 – ( a – b ) = 15 – 10 = 5 A= (x2 + 3x – 1) + ( - 3x )= x2 – 1x2 – 15、若 a 是一个有理数，则下列式子中一定
正确的是 （ ）
(A) 10a > a (B) a < a
(C) a > 0 (D) ≥ 04、一列数
按此规律写下去，第n个数是 。D6、填写下表，并观察下列两个代数式的值
的变化情况：(1) n 为何值时，两代数式的值相等？(2) 随着 n 逐渐变大， n2与7n+8 的差如何变
化？解： 原式 = a – 2b 当 a = 6 , b = - 2 时

原式 = a – 2b = ×6 – 2 ×( - 2 )=2439.如下边的一排方格中，每一个字母表示
一个数，已知其中任何连续三个方格中
的数之和为 19 ， 求 ( A + B ) – ( C - D ) 的值。课后巩固：1、A、B两地相距s千米，甲车以每小时a千米的速度，乙以每小时b千米的速度分别从A、B两地相向而行，经_______小时相遇。
2、数a的 2倍与b的3倍的差，用代数式表示为____________；
3、甲数是乙数的2倍还多3，设甲数是x，则乙数表示为__________；
4、三个连续整数，中间一个数为n，则另外两个整数表示为________,__________.
5、据统计，12头大象一天能吃掉的食物可以供给1000只老鼠吃600天，那么x头大象一天的食物可以供给1000只老鼠吃_________天。6、当x=3时，代数式3x-1的值是_____；
7、当a=-5时，代数式-4a-3的值是_____;
8、若│x+2│+│y-3│=0，则3x-y=__；
9、单项式-x3y4的系数是___，次数是___;
10、多项式3xy-4x2y3-5xy2+7中的第一项的系数是______；第三项是_______；最高次数的项是________，这个多项式是_____次______项式。11、某居民统计了家里的用水量x（立方米）与应缴水费w（元）之间的关系如下表所示。
（1）写出用水量x（立方米）与水费x（元）之间的关系式。
（2）计算用水量是35立方米时的水费是多少元？通过本节课的学习 ：
1、你学到了哪些知识？2、你有什么收获？