4.1比例线段（2）学案

4.1比例线段(2)学案
学习目标：
1.了解两条线段的比和比例线段的概念；
2.能根据条件写出比例线段；
3.会运用比例线段解决简单的实际问题。
教学重点：比例线段的概念.
教学难点：例3要求根据具体问题发现等量关系，找出比例式，有一定的隐蔽性，是本节教学的难点.
学习准备：
1.若5a=2b，则 . 2. 已知x∶3=4∶5，则x= .
3. 等腰直角三角形斜边上的高与斜边的比值是 .
一、探索研讨
【活动1】
1.如何定义两线段的比呢？什么是比例线段？
我们规定:两条线段的长度比叫做这两条线段的比
2.在直角坐标系内作使得：、、；作使得：、.
线段 ， ，则线段与的比就是 ，记做 .
由图得：从到是一个 ，可得 = .
归纳：一般地，四条线段a、b、c、d中，如果a与b的比等于c与d比，即 ，那么这四条线段a、b、c、d叫做成比例线段，简称比例线段。
【活动2】
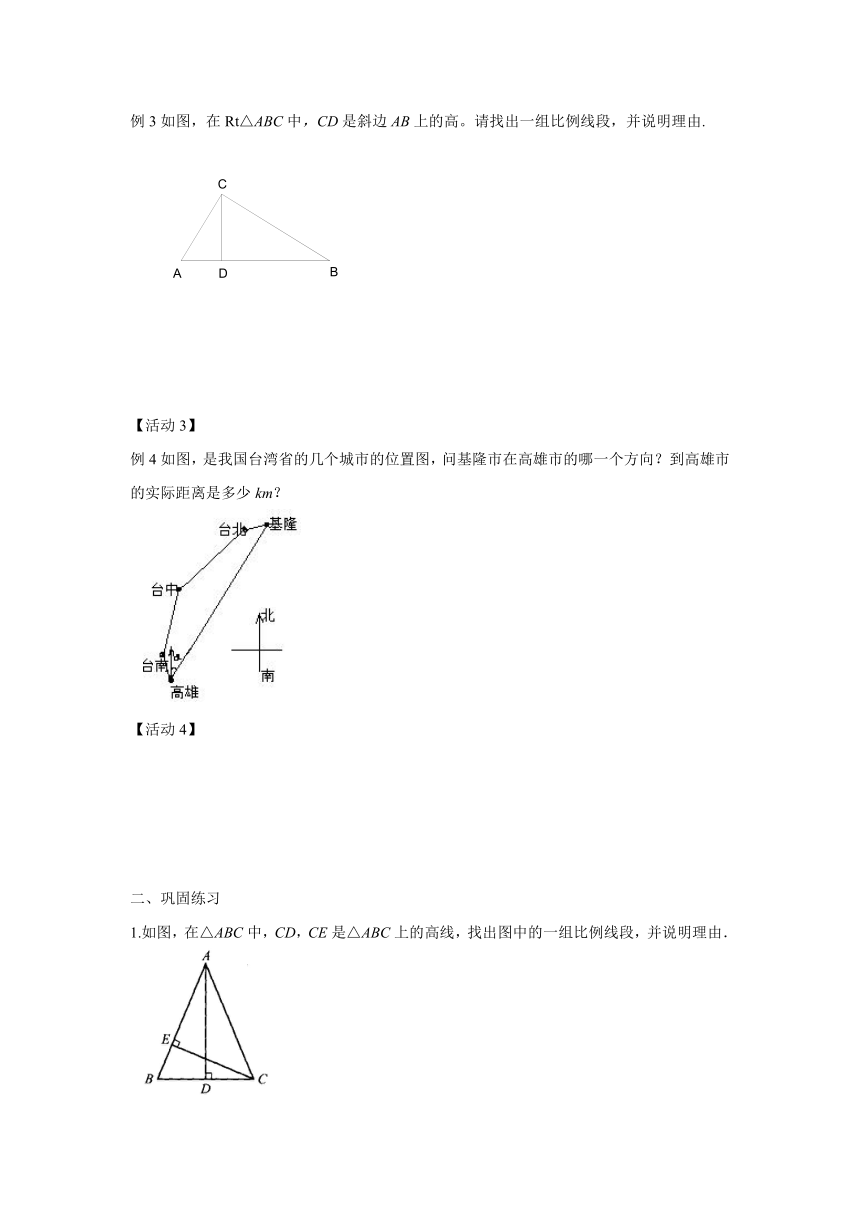
例3如图，在Rt△ABC中，CD是斜边AB上的高。请找出一组比例线段，并说明理由.
【活动3】
例4如图，是我国台湾省的几个城市的位置图，问基隆市在高雄市的哪一个方向？到高雄市的实际距离是多少km？
【活动4】
二、巩固练习
1.如图，在△ABC中，CD，CE是△ABC上的高线，找出图中的一组比例线段，并说明理由．
2.在中国地理地图册上，连结上海、香港、台湾三地构成一个三角形，用刻度尺测得它们之间的距离如图所示．飞机从台湾直飞上海的距离约为1 286千米，那么飞机从台湾绕道香港再到上海的飞行距离约为多少千米？
三、当堂检测
1、如图，Rt△ABC内接于⊙O，,求：
（1） （2）
2．在如图三个长方形中，哪两个长方形的长和宽是比例线段？
3．如图，在平行四边形ABCD中，DE⊥AB,DF⊥BC,找出图中的一组比例线段（小写字母表示相应的线段），并说明理由。
第3题 第4题
4．如图，DE是△ABC的中位线，请尽可能多地写出比例线段。
四、反思归纳
1、本节课学习的内容：
2、数学思想方法归纳：
上海
台湾
香港
5.4cm
3.6cm
3cm