2022-2023学年浙教版数学七年级上册 6.6 角的大小比较 课件 (共20张PPT)
文档属性
| 名称 | 2022-2023学年浙教版数学七年级上册 6.6 角的大小比较 课件 (共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 09:40:12 | ||
图片预览





文档简介
(共20张PPT)
角的大小比较
由于度数的不同,角有大小之分.角的大小比较同线
段的长短比较类似,都可用叠合法和度量法.
已知∠A=30°,∠B=28°,∠C=35°,用“<”、
将三个角连接起来:____________________.
2. 角按照度数为分为直角、锐角、钝角.
等于_______的角是直角,_______直角的角是锐角,
____________________的角是钝角.
大于直角而小于平角
∠B<∠A<∠C
90°
小于
一般地,如果两个角的______相等,我们说这两个角
相等.如∠A=30°,∠B=30°,就说∠A与∠B相等,
记作__________,如果两个角的度数不相等,我们就
说______较大的角较大;反之,度数较小的角较小.
如∠A=30°,∠C=45°,则说∠A小于∠C,记作
__________.
2. 用叠合法比较两个角的大小时,要把两个角的______
和一条边互相重合.
度数
∠A=∠B
度数
∠A<∠C
顶点
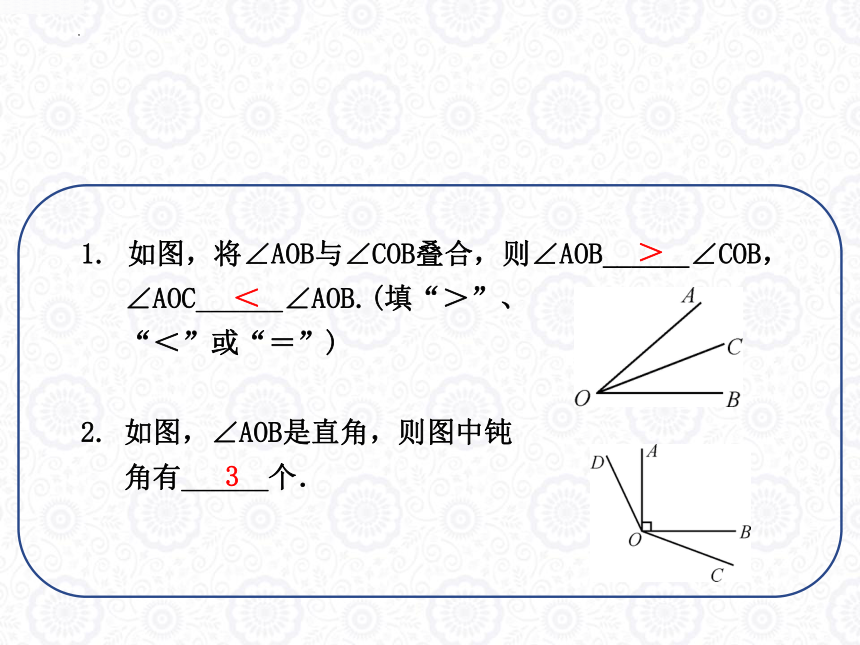
如图,将∠AOB与∠COB叠合,则∠AOB______∠COB,
∠AOC______∠AOB.(填“>”、
“<”或“=”)
2. 如图,∠AOB是直角,则图中钝
角有______个.
>
<
3
3. 在等腰△ABC中,AB与AC是腰,则图中
相等的角是__________.
4. 两块三角板如图放置,则图中锐角的
个数为______个.
7
∠B=∠C
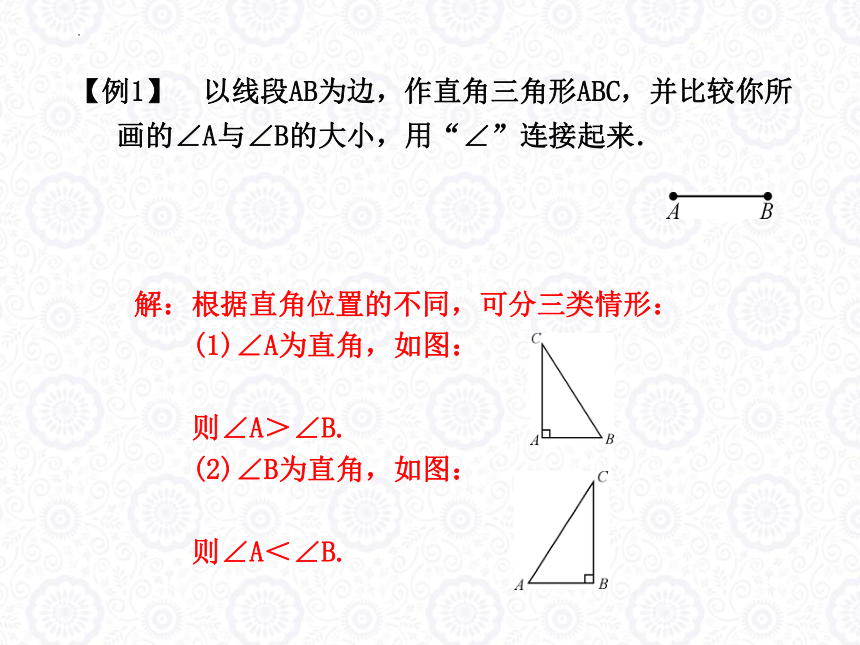
【例1】 以线段AB为边,作直角三角形ABC,并比较你所
画的∠A与∠B的大小,用“∠”连接起来.
解:根据直角位置的不同,可分三类情形:
(1)∠A为直角,如图:
则∠A>∠B.
(2)∠B为直角,如图:
则∠A<∠B.
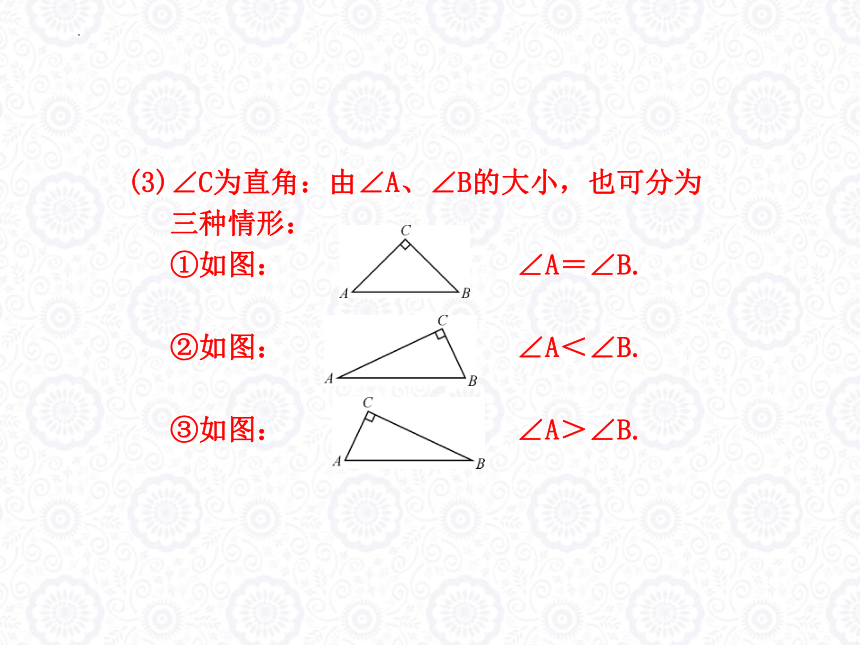
(3)∠C为直角:由∠A、∠B的大小,也可分为
三种情形:
①如图: ∠A=∠B.
②如图: ∠A<∠B.
③如图: ∠A>∠B.
变式训练1 如图,∠A=90°,在∠A的基础上任意作
一个长方形ABCD.
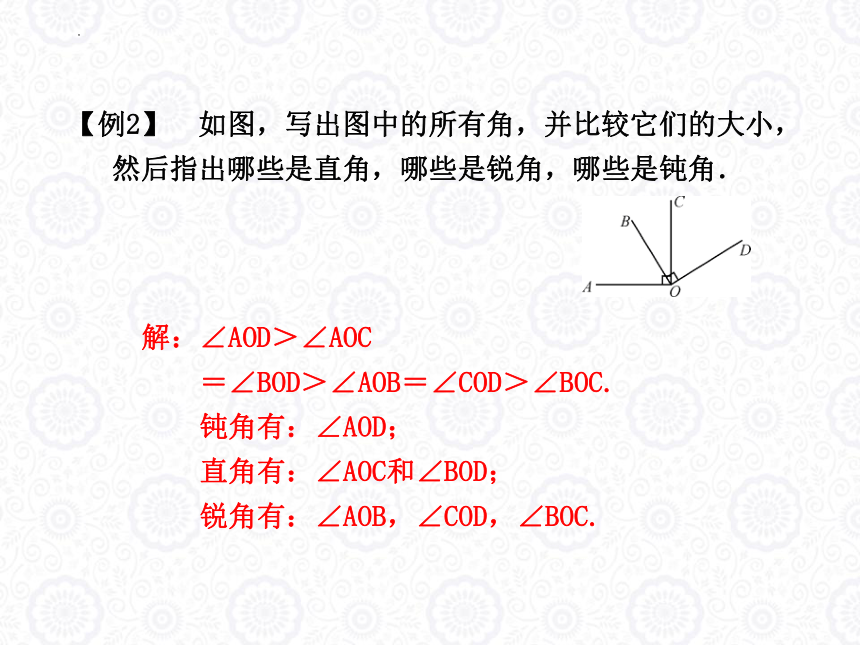
【例2】 如图,写出图中的所有角,并比较它们的大小,
然后指出哪些是直角,哪些是锐角,哪些是钝角.
解:∠AOD>∠AOC
=∠BOD>∠AOB=∠COD>∠BOC.
钝角有:∠AOD;
直角有:∠AOC和∠BOD;
锐角有:∠AOB,∠COD,∠BOC.
解:∵α、β均为锐角,∴α+β<180°,
∴只有甲正确.
变式训练2 已知α、β是锐角,甲乙丙丁四人计算 (α+β)
的结果依次为:44°、45°、46°、47°,其中只有一人正
确,请指出并说明理由.
归纳总结
角类似于线段也是可以进行大小比较的,角的大小
比较看度数的大小,而线段的大小比较看线段长度
的大小.
2. 角的大小比较方法类似于线段的长短比较,也是采
用叠合法与度量法.
3. 在判断一个角是钝角还是锐角时,要与直角作大小
比较,大于直角小于平角的角是钝角,小于直角的
角是锐角.
(一)选择题
1. 一副三角尺有6个角,其中最小角的度数是 ( )
A. 30° B. 45°
C. 60° D. 90°
A
2. 如图,三角尺ABC中,∠C是直角,∠A=30°,则以下
数量关系不正确的是 ( )
A. ∠A<∠B B. ∠A+∠B=90°
C. ∠C>∠B D. ∠A=∠B
D
3. 如图,在长方形ABCD中,连接DB,则图中锐角的
个数有 ( )
A. 1个 B. 2个
C. 3个 D. 4个
D
4. 如图,射线OB、OC将∠AOD分为三部分,如果∠AOC<
∠BOD,则∠AOB与∠COD的大小关系是 ( )
A. ∠AOB<∠COD
B. ∠AOB=∠COD
C. ∠AOB>∠COD
D. 无法判断
A
(二 )填空题
5. 一个三角形最多有_____个锐角,最少有_____个锐角.
6. 如图,∠AOB是直角,OC是直角内部的
一条射线,且∠COB=32°,则∠AOC=
______,∠AOC______∠COB(填“>”、
“<”或“=”)
7. 已知∠α=30°,∠β=2∠α+10°,则∠β=_____.
70°
3
2
58°
>
(三)解答题
8. 任意作一个直角,一个小于60°的锐角和一个大于
120°的钝角.
9. 如图,△ABC是等腰三角形,比较∠BAC、∠CAD、
∠BAD、∠ADB的大小,并说出其中的锐角、直角
和钝角.
解:∠BAC>∠ADB>∠CAD=∠BAD.
锐角:∠CAD,∠BAD;
直角:∠ADB;
钝角:∠BAC.
10. 比较下列三个时刻的时针与分针所成的角的大小,并说明
理由:①3∶00;②9∶30;③7∶20.
解:当3∶00时:针指向3,分针指向12,
∴时针与分针成90°.
当9∶30时:时针指向9与10的中点,分针指向6,
∴时针与分针成105°.
当7∶20时:时针指向7与8之间的靠近7的 处,
分针指向4,
∴时针与分针成100°.
11. 在12点到13点之间,何时时钟的时针与分针成直角?
解:时针每分钟走0.5°,分针走分钟走6°.
设x分钟后两针成直角,得:
角的大小比较
由于度数的不同,角有大小之分.角的大小比较同线
段的长短比较类似,都可用叠合法和度量法.
已知∠A=30°,∠B=28°,∠C=35°,用“<”、
将三个角连接起来:____________________.
2. 角按照度数为分为直角、锐角、钝角.
等于_______的角是直角,_______直角的角是锐角,
____________________的角是钝角.
大于直角而小于平角
∠B<∠A<∠C
90°
小于
一般地,如果两个角的______相等,我们说这两个角
相等.如∠A=30°,∠B=30°,就说∠A与∠B相等,
记作__________,如果两个角的度数不相等,我们就
说______较大的角较大;反之,度数较小的角较小.
如∠A=30°,∠C=45°,则说∠A小于∠C,记作
__________.
2. 用叠合法比较两个角的大小时,要把两个角的______
和一条边互相重合.
度数
∠A=∠B
度数
∠A<∠C
顶点
如图,将∠AOB与∠COB叠合,则∠AOB______∠COB,
∠AOC______∠AOB.(填“>”、
“<”或“=”)
2. 如图,∠AOB是直角,则图中钝
角有______个.
>
<
3
3. 在等腰△ABC中,AB与AC是腰,则图中
相等的角是__________.
4. 两块三角板如图放置,则图中锐角的
个数为______个.
7
∠B=∠C
【例1】 以线段AB为边,作直角三角形ABC,并比较你所
画的∠A与∠B的大小,用“∠”连接起来.
解:根据直角位置的不同,可分三类情形:
(1)∠A为直角,如图:
则∠A>∠B.
(2)∠B为直角,如图:
则∠A<∠B.
(3)∠C为直角:由∠A、∠B的大小,也可分为
三种情形:
①如图: ∠A=∠B.
②如图: ∠A<∠B.
③如图: ∠A>∠B.
变式训练1 如图,∠A=90°,在∠A的基础上任意作
一个长方形ABCD.
【例2】 如图,写出图中的所有角,并比较它们的大小,
然后指出哪些是直角,哪些是锐角,哪些是钝角.
解:∠AOD>∠AOC
=∠BOD>∠AOB=∠COD>∠BOC.
钝角有:∠AOD;
直角有:∠AOC和∠BOD;
锐角有:∠AOB,∠COD,∠BOC.
解:∵α、β均为锐角,∴α+β<180°,
∴只有甲正确.
变式训练2 已知α、β是锐角,甲乙丙丁四人计算 (α+β)
的结果依次为:44°、45°、46°、47°,其中只有一人正
确,请指出并说明理由.
归纳总结
角类似于线段也是可以进行大小比较的,角的大小
比较看度数的大小,而线段的大小比较看线段长度
的大小.
2. 角的大小比较方法类似于线段的长短比较,也是采
用叠合法与度量法.
3. 在判断一个角是钝角还是锐角时,要与直角作大小
比较,大于直角小于平角的角是钝角,小于直角的
角是锐角.
(一)选择题
1. 一副三角尺有6个角,其中最小角的度数是 ( )
A. 30° B. 45°
C. 60° D. 90°
A
2. 如图,三角尺ABC中,∠C是直角,∠A=30°,则以下
数量关系不正确的是 ( )
A. ∠A<∠B B. ∠A+∠B=90°
C. ∠C>∠B D. ∠A=∠B
D
3. 如图,在长方形ABCD中,连接DB,则图中锐角的
个数有 ( )
A. 1个 B. 2个
C. 3个 D. 4个
D
4. 如图,射线OB、OC将∠AOD分为三部分,如果∠AOC<
∠BOD,则∠AOB与∠COD的大小关系是 ( )
A. ∠AOB<∠COD
B. ∠AOB=∠COD
C. ∠AOB>∠COD
D. 无法判断
A
(二 )填空题
5. 一个三角形最多有_____个锐角,最少有_____个锐角.
6. 如图,∠AOB是直角,OC是直角内部的
一条射线,且∠COB=32°,则∠AOC=
______,∠AOC______∠COB(填“>”、
“<”或“=”)
7. 已知∠α=30°,∠β=2∠α+10°,则∠β=_____.
70°
3
2
58°
>
(三)解答题
8. 任意作一个直角,一个小于60°的锐角和一个大于
120°的钝角.
9. 如图,△ABC是等腰三角形,比较∠BAC、∠CAD、
∠BAD、∠ADB的大小,并说出其中的锐角、直角
和钝角.
解:∠BAC>∠ADB>∠CAD=∠BAD.
锐角:∠CAD,∠BAD;
直角:∠ADB;
钝角:∠BAC.
10. 比较下列三个时刻的时针与分针所成的角的大小,并说明
理由:①3∶00;②9∶30;③7∶20.
解:当3∶00时:针指向3,分针指向12,
∴时针与分针成90°.
当9∶30时:时针指向9与10的中点,分针指向6,
∴时针与分针成105°.
当7∶20时:时针指向7与8之间的靠近7的 处,
分针指向4,
∴时针与分针成100°.
11. 在12点到13点之间,何时时钟的时针与分针成直角?
解:时针每分钟走0.5°,分针走分钟走6°.
设x分钟后两针成直角,得:
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
