2022--2023学年浙教版数学七年级上册 1.3 绝对值 课件(共13张PPT)
文档属性
| 名称 | 2022--2023学年浙教版数学七年级上册 1.3 绝对值 课件(共13张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 764.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 00:00:00 | ||
图片预览





文档简介
(共13张PPT)
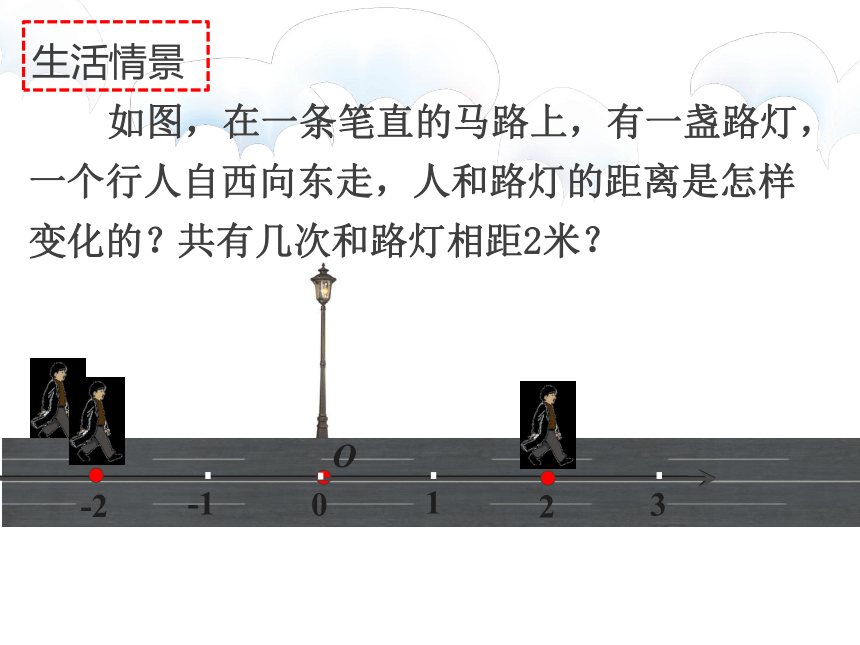
生活情景
如图,在一条笔直的马路上,有一盏路灯,一个行人自西向东走,人和路灯的距离是怎样变化的?
O
-2
2
-1
0
1
3
-3
共有几次和路灯相距2米?
1.3 绝对值
揭示定义
一般地,在数轴上表示数a的点到原点的距离叫做a的绝对值,记作|a|。
在数轴上表示-2的点到0的距离是2,
同样的,在数轴上表示3的点到0的距离是3,
+3的绝对值是3,写作|+3|=3或|3|=3。
-2
-1
0
1
2
3
-3
2
3
所以-2的绝对值就是2,写作|-2|=2。
什么是绝对值呢?
初步认识
借助数轴,从左到右求出刚才表示在数轴上,的几个数的绝对值。
观察并思考:
从绝对值的含义和刚才的计算中,你发现一个数的绝对值的结果有什么特点?
绝对值的结果是正数或0,具有非负性。
结果和原先的数对比,你还发现了什么规律?
练习
(1)说出下列各数的绝对值:
问题1:绝对值等于5的数还有吗?
问题2: 的绝对值是什么?
有,-5和5的绝对值都是5
再次认识
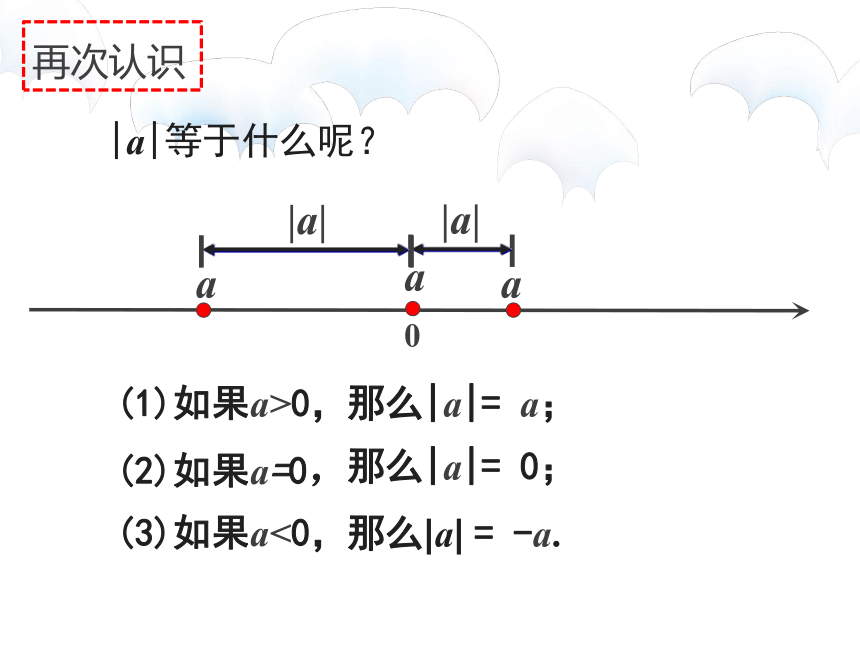
|a|等于什么呢?
(1)如果a>0,
那么|a|= a;
(2)如果a=0,
那么|a|= 0;
(3)如果a<0,
那么|a| = -a.
0
a
|a|
a
a
|a|
①一个数的绝对值越大,表示它的点在数轴上越靠右。( )
③绝对值等于4的数就是4。( )
巩固练习
(2)判断并说明理由:
②负数的绝对值小于正数的绝对值。( )
×
×
×
巩固练习
(3)计算
应用练习
(4)说理
正式比赛对所用排球的质量有严格的规定。下面是6个排球的质量检测结果(记超过规定质量的克数为正):
①-2.3,②+1,③-1.9,④+3,⑤+1.7,⑥-0.7
哪个排球的质量好一些,并用绝对值的知识说明。
拓展练习
绝对值小于3.5的数有 个;
绝对值小于3.5的整数有 个;
绝对值小于3.5的负整数有 个;
绝对值小于3.5,大于1的整数有 个;
无数
7
3
4
绝对值小于3.5,(补充一个条件) 只有1个,
这个数是 。
课堂小结
通过今天这节课,你有哪些收获和感受
趣说绝对值
绝对值号就像两个卫兵站岗,不论什么身份(正数、负数、0)都可以进,但只有改造合格的人才能出来。如果遇到身份不明的人,就要仔细审查,考虑结果。
延伸练习
|a|表示的是a到0的距离,它也可以看作是|a-0|。按照这个推理,|a-2|表示的是什么意思?
如果a=3,那么|a-2|等于多少?
|a+2|等于什么?
|a+2|可以看成a到几的距离?
表示a到2的距离
|3-2|=1
|3+2|=5
-2
-1
0
1
2
3
-3
3
2
|a+2|=|a-(-2)|
再见
生活情景
如图,在一条笔直的马路上,有一盏路灯,一个行人自西向东走,人和路灯的距离是怎样变化的?
O
-2
2
-1
0
1
3
-3
共有几次和路灯相距2米?
1.3 绝对值
揭示定义
一般地,在数轴上表示数a的点到原点的距离叫做a的绝对值,记作|a|。
在数轴上表示-2的点到0的距离是2,
同样的,在数轴上表示3的点到0的距离是3,
+3的绝对值是3,写作|+3|=3或|3|=3。
-2
-1
0
1
2
3
-3
2
3
所以-2的绝对值就是2,写作|-2|=2。
什么是绝对值呢?
初步认识
借助数轴,从左到右求出刚才表示在数轴上,的几个数的绝对值。
观察并思考:
从绝对值的含义和刚才的计算中,你发现一个数的绝对值的结果有什么特点?
绝对值的结果是正数或0,具有非负性。
结果和原先的数对比,你还发现了什么规律?
练习
(1)说出下列各数的绝对值:
问题1:绝对值等于5的数还有吗?
问题2: 的绝对值是什么?
有,-5和5的绝对值都是5
再次认识
|a|等于什么呢?
(1)如果a>0,
那么|a|= a;
(2)如果a=0,
那么|a|= 0;
(3)如果a<0,
那么|a| = -a.
0
a
|a|
a
a
|a|
①一个数的绝对值越大,表示它的点在数轴上越靠右。( )
③绝对值等于4的数就是4。( )
巩固练习
(2)判断并说明理由:
②负数的绝对值小于正数的绝对值。( )
×
×
×
巩固练习
(3)计算
应用练习
(4)说理
正式比赛对所用排球的质量有严格的规定。下面是6个排球的质量检测结果(记超过规定质量的克数为正):
①-2.3,②+1,③-1.9,④+3,⑤+1.7,⑥-0.7
哪个排球的质量好一些,并用绝对值的知识说明。
拓展练习
绝对值小于3.5的数有 个;
绝对值小于3.5的整数有 个;
绝对值小于3.5的负整数有 个;
绝对值小于3.5,大于1的整数有 个;
无数
7
3
4
绝对值小于3.5,(补充一个条件) 只有1个,
这个数是 。
课堂小结
通过今天这节课,你有哪些收获和感受
趣说绝对值
绝对值号就像两个卫兵站岗,不论什么身份(正数、负数、0)都可以进,但只有改造合格的人才能出来。如果遇到身份不明的人,就要仔细审查,考虑结果。
延伸练习
|a|表示的是a到0的距离,它也可以看作是|a-0|。按照这个推理,|a-2|表示的是什么意思?
如果a=3,那么|a-2|等于多少?
|a+2|等于什么?
|a+2|可以看成a到几的距离?
表示a到2的距离
|3-2|=1
|3+2|=5
-2
-1
0
1
2
3
-3
3
2
|a+2|=|a-(-2)|
再见
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
