3.3圆心角（1）学案

3.3圆心角(1)学案
学习目标：
1、经历探索圆的中心对称性和旋转不变性的过程.
2、理解圆心角的概念，并掌握“在同圆和等圆中，相等的圆心角所对的弧相等，所对的弦相等”的定理（圆心角定理）.
3、体验利用旋转变换来研究圆的性质的思想方法.
教学重点：圆心角定理
教学难点：根据圆的旋转不变性推出圆心角定理，需用到图形的旋转变换.
学习准备：
一、探索研讨
【活动1】
1.动手画圆，对折、我们发现：圆是 图形和 图形.
2.我们规定圆心角和弦心距的概念：
圆心角定义：顶点在圆心的角叫圆心角．
弦心距定义：从圆心到弦的距离叫做弦心距．
【活动2】
1.如图，在⊙O中，已知圆心角∠AOB和圆心角∠COD相等，那么两个圆心角所对的两段弧、两条弦、两条弦心距之间有什么数量关系？为什么
2.一般的，圆有下面的性质（圆心角定理）：
在同圆或等圆中，相等的圆心角所对的 相等，所对的 相等，所对的 也相等.
3.几何语言：
已知：如图，AB、CD是⊙O的两条弦，OE、OF为AB、CD的弦心距，根据本节定理及推论填空：
∵∠AOB=∠COD
∴_____ = ____，___ = _____，_____ = __ __.
【活动3】
例1.用直尺和圆规把⊙O四等分
【活动4】
在同圆中，相等的圆心角所对的弧相等，所以我们规定把1°圆心角所对的弧叫做1°弧.这样，n°的圆心角所对的弧就是n°的弧
二、巩固练习
1. 如图，MN为⊙O的弦，∠M=50°，则圆心角∠MON等于（ ）
A. 50° B. 55° C. 65° D. 80°
2. 如图，⊙O中，∠AOB=∠COD，则AC= ，= .
3. 若等边△ABC内接于⊙O，则的度数是 .
三、当堂检测
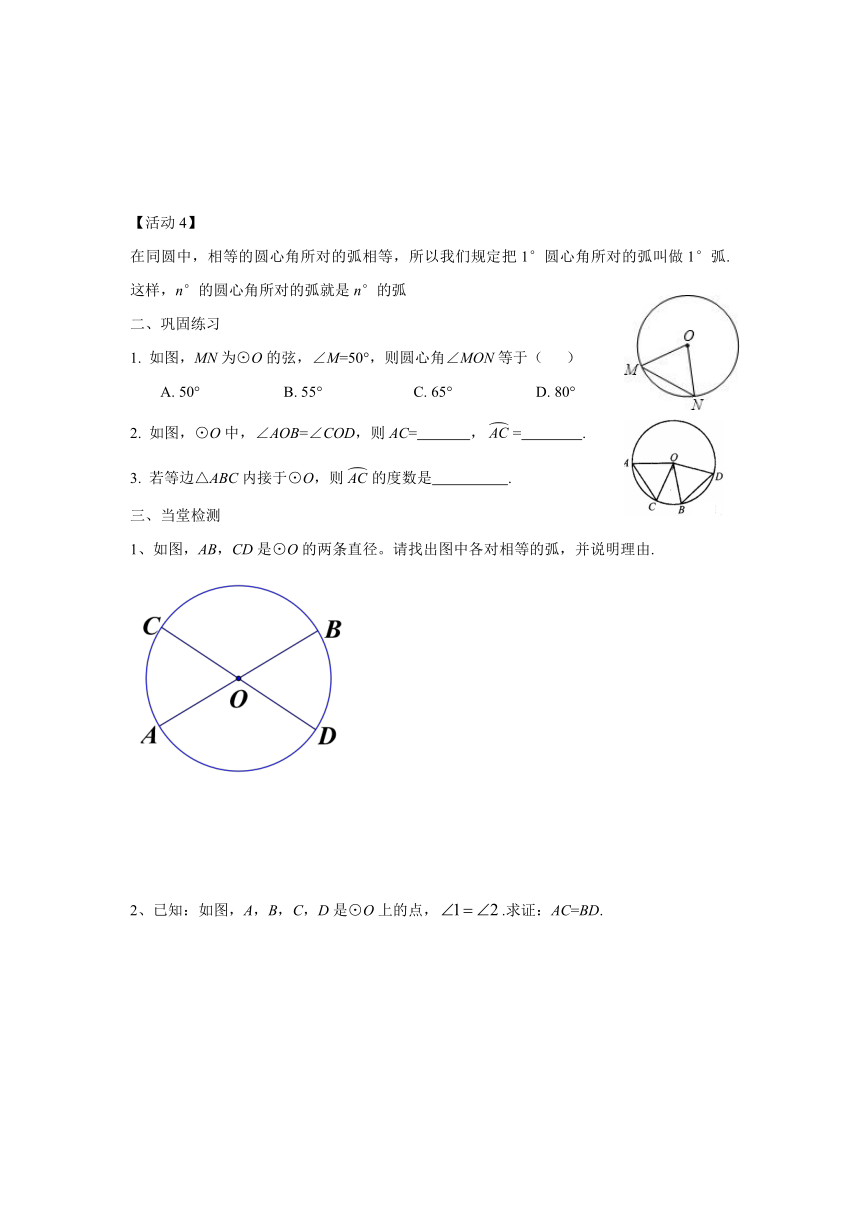
1、如图，AB，CD是⊙O的两条直径。请找出图中各对相等的弧，并说明理由.
2、已知：如图，A，B，C，D是⊙O上的点，.求证：AC=BD.
3、如图，⊙O的直径AB垂直于弦CD，AB，CD相交于点E，.求弧BC，弧AD的度数.
4、任意画一个圆，作出它的一个内接等边三角形.
5、观察如图的图案，画法中运用了圆的几等分？请利用圆的等分制作一幅图案.
四、反思归纳
1、本节课学习的内容：
2、数学思想方法归纳：