3.4圆周角（1）学案

3.4圆周角(1)学案
学习目标：1、理解圆周角的概念.
2、经历探索圆周角定理的过程
3、掌握圆周角定理和它的推论.
4、会运用圆周角定理及其推论解决简单的几何问题.
学习重点：圆周角定理
学习难点：圆周角定理的证明
学习准备：
1、已知点A、B、C、D、E是⊙O的五等分点，则∠AOC= 度。
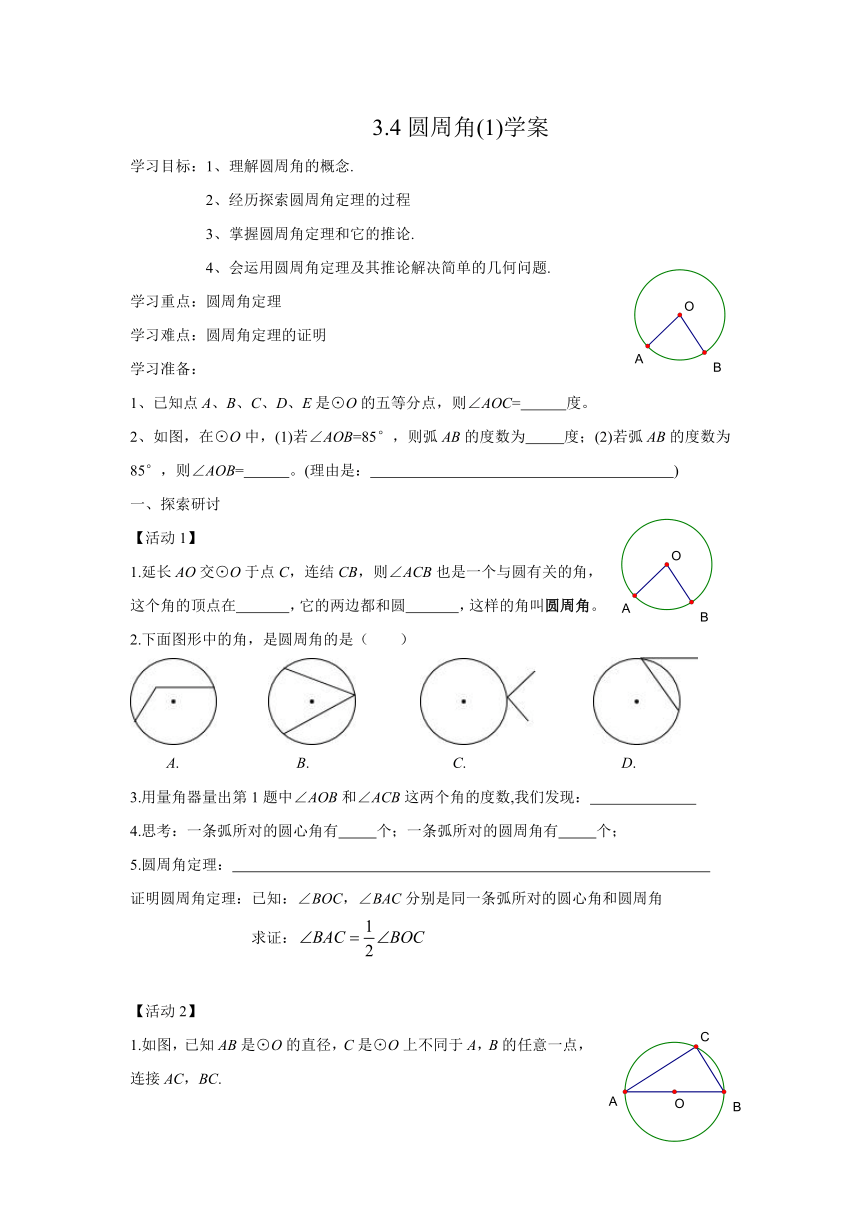
2、如图，在⊙O中，(1)若∠AOB=85°，则弧AB的度数为 度；(2)若弧AB的度数为85°，则∠AOB= 。(理由是： )
一、探索研讨
【活动1】
1.延长AO交⊙O于点C，连结CB，则∠ACB也是一个与圆有关的角，这个角的顶点在 ，它的两边都和圆 ，这样的角叫圆周角。
2.下面图形中的角，是圆周角的是（　　）
3.用量角器量出第1题中∠AOB和∠ACB这两个角的度数,我们发现：
4.思考：一条弧所对的圆心角有 个；一条弧所对的圆周角有 个；
5.圆周角定理：
证明圆周角定理：已知：∠BOC，∠BAC分别是同一条弧所对的圆心角和圆周角
求证：
【活动2】
1.如图，已知AB是⊙O的直径，C是⊙O上不同于A，B的任意一点，连接AC，BC.
求证：∠C是直角.
我们又得到圆周角的一个推论：
半圆（或直径）所对的圆周角是 ； 90°的圆周角所对的弦是 .
【活动3】
例1.如图；四边形ABCD的四个顶点在⊙O上.
求证:∠B+∠D = 180°.
二、巩固练习
1. 任意写出图中的一个圆周角 .
2. 已知一条弧的度数为40°，那么它所对的圆周角的度数是 .
3. 如图，点A，B，C是⊙O上的三点，若∠BOC=50°，则∠A的度数为 ．
4. 已知Rt△ABC的两直角边的长分别为6cm和8cm，则它的外接圆的半径为_________cm.
三、当堂检测
1、一条弧所对的圆心角的度数为。求这条弧的度数和这条弧所对的圆周角的度数。
2．如图，是⊙O的圆周角，=，求的度数。
3.如图，在⊙O中，，，求的度数
。
4、如图，四边形ABCD内接于⊙O，，，点E在AB的延长线上，求的度数.
5.如图，C是弧AB上的一点，。求的度数.
6、如图，是⊙O的内接三角形，AD是⊙O的直径，。求的度数。
7、已知：如图，OA是⊙O的半径，以OA为直径的⊙C与⊙O的弦相交于点D。求证：AD=DB.
四、反思归纳
1、本节课学习的内容：
2、数学思想方法归纳：
A.
B.
C.
D.