3.4圆周角(2)学案

3.4圆周角(2)学案
学习目标：
1.经历探索圆周角定理的另一个推论的过程.
2.掌握圆周角定理的推论“在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等”
3.会运用上述圆周角定理的推论解决简单几何问题.
学习重点：圆周角定理的推论”在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等
学习难点：例3涉及圆内角与圆外角与圆周角的关系,思路较难形成,表述也有一定的困难
例4的辅助线的添法.
学习准备：
1.100 的弧所对的圆心角等于_______，所对的圆周角等于_______.
2.如图，在⊙O中，∠BAC=35 ，则∠BOC=________.
3.如图，⊙O中，∠ACB = 130 ，则∠AOB=______
一、探索研讨
【活动1】
1.我们知道，在同圆或等圆中，等弧所对的圆心角相等，相等的圆心角所对的弧也相等，那么根据圆周角定理，在在同圆或等圆中，同弧或等弧所对的圆周角有什么数量关系，相等的圆周角所对的弧又有什么数量关系？
所以我们可以得到圆周角定理的一个推论：
在同圆或等圆中，同弧或等弧所对的圆周角 ，相等的圆周角所对的弧 .
2. 已知：如图，∠APC=∠CPB=60°. 求证：△ABC是等边三角形
【活动2】
例2.已知：如图，在△ABC中，AB=AC, 以AB为直径的圆交BC于D,交AC于E,
求证：
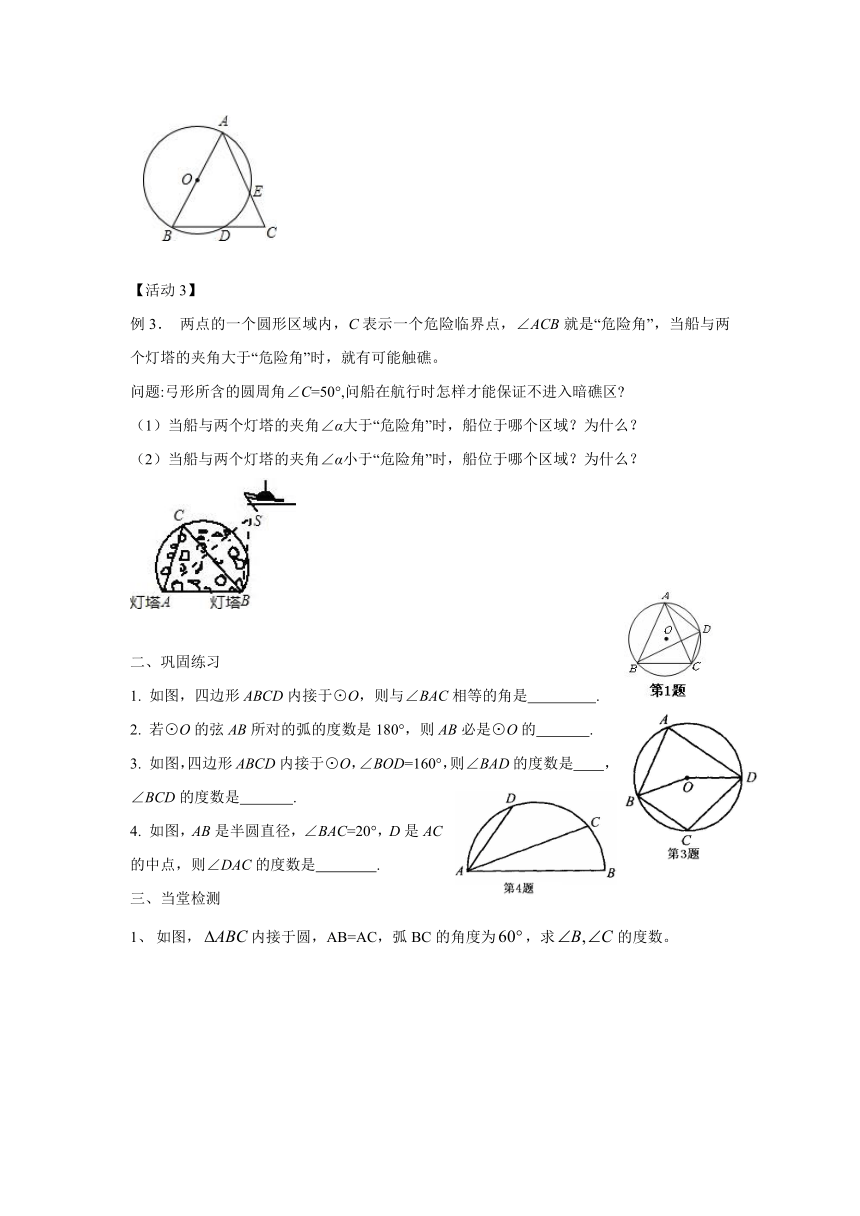
【活动3】
例3． 两点的一个圆形区域内，C表示一个危险临界点，∠ACB就是“危险角”，当船与两个灯塔的夹角大于“危险角”时，就有可能触礁。
问题:弓形所含的圆周角∠C=50°,问船在航行时怎样才能保证不进入暗礁区
（1）当船与两个灯塔的夹角∠α大于“危险角”时，船位于哪个区域？为什么？
（2）当船与两个灯塔的夹角∠α小于“危险角”时，船位于哪个区域？为什么？
二、巩固练习
1. 如图，四边形ABCD内接于⊙O，则与∠BAC相等的角是 .
2. 若⊙O的弦AB所对的弧的度数是180°，则AB必是⊙O的 .
3. 如图，四边形ABCD内接于⊙O，∠BOD=160°，则∠BAD的度数是 ，∠BCD的度数是 .
4. 如图，AB是半圆直径，∠BAC=20°，D是AC的中点，则∠DAC的度数是 .
三、当堂检测
如图，内接于圆，AB=AC，弧BC的角度为，求的度数。
已知：如图，AB是⊙O的直径，弦AC与半径OD平行。求证：。
如图，梯形ABCD内接于⊙O。这个梯形是等腰梯形吗？请说明理由。
已知：如图，在⊙O中，AB=CD。求证：。
一个圆形人工湖如图所示，弦AB是弦上的一座桥。已知桥AB长100m，测得圆周角 ，求这个人工湖的直径。
如图，AB是⊙O的直径，弦于点E，G是弧AC上任意一点。延长AG，与DC的延长线相交于点F，连接AD,GD,CG。找出图中所有和相等的角，并说明理由。
四、反思归纳
1、本节课学习的内容：
2、数学思想方法归纳：
第2题
第3题