3.5弧长及扇形的面积（2）学案

3.5弧长及扇形的面积(2)学案
学习目标：1、经历探索扇形面积计算公式的过程。
2、掌握扇形面积计算公式，并会应用公式解决问题。
学习重点：扇形面积计算公式
学习难点：例4中涉及弓形面积计算还有流量和流速等实际背景
学习准备：
在一块空旷的草地上有一根柱子,柱子上拴着一条长3m的绳子,绳子的另一端拴着一只狗.
(1)这只狗的最大活动区域有多大
(2)如果这只狗只能绕柱子转过n°角,那么它的最大活动区域有多大
一、探索研讨
【活动1】
1、已知圆的半径为6cm，则圆心角为90°的扇形面积为 ；圆心角为120°的扇形面积为 ；圆心角为240°的扇形面积为 ；弧长为7.2cm的扇形面积为 ；
2、如果圆的半径为R，则圆的面积为 ，
1°的圆心角对应的扇形面积为 ，
2°的圆心角对应的扇形面积为 ，
n°的圆心角对应的扇形面积为 ，
扇形的面积公式：
如果扇形的半径为R，圆心角为n°，扇形的弧长为l，那么扇形面积的计算公式为：
= .
4、在弧长公式和扇形面积公式这两个公式中，弧长和扇形面积都和圆心角n°、半径R有关系，因此l 和S之间也有一定的关系，你能猜得出吗
【活动2】练习：
1、已知扇形的圆心角为120°，半径为2，则这个扇形的面积__ _．
2、已知扇形面积为，圆心角为120°，则这个扇形的半径R=_ ___．
3、已知半径为2的扇形，面积为 ，则它的圆心角的度数=__ __．
4、已知半径为2cm的扇形，其弧长为 ，则这个扇形的面积， ．
【活动3】
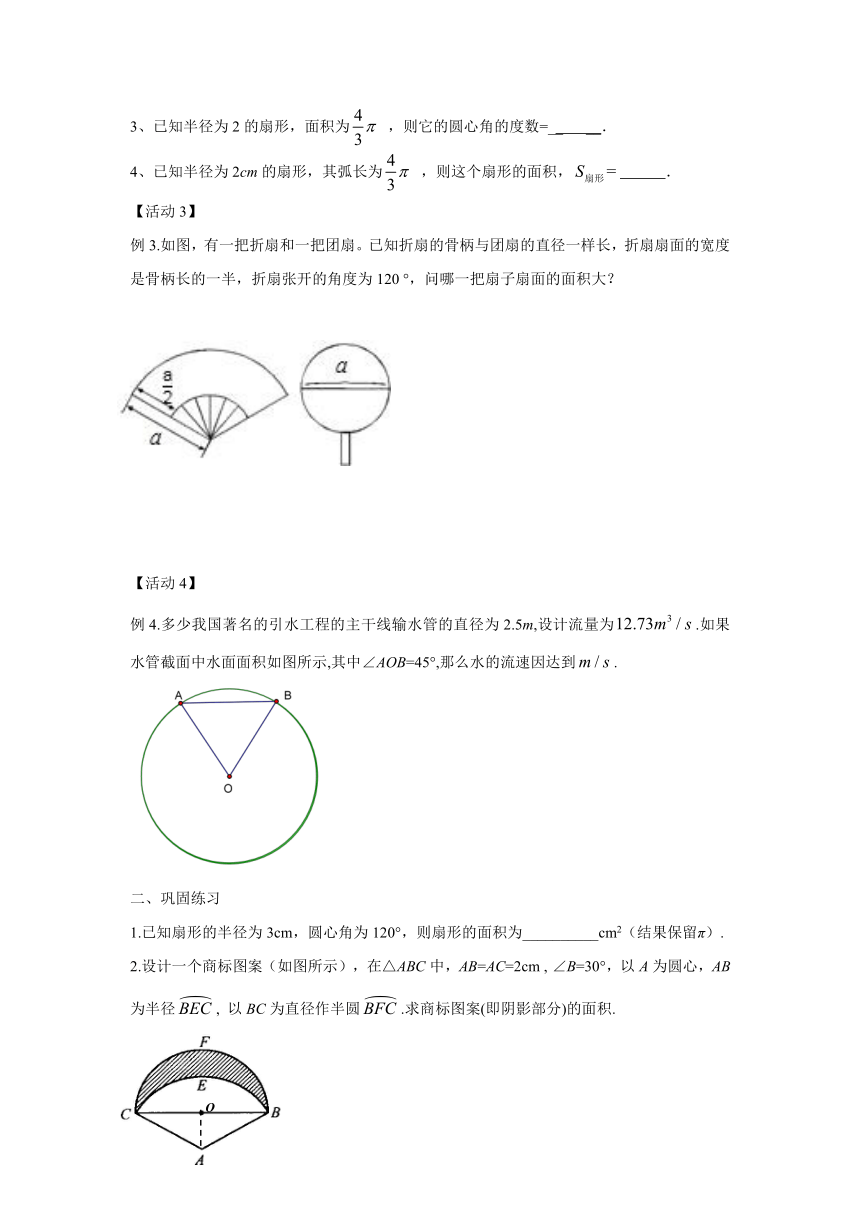
例3.如图，有一把折扇和一把团扇。已知折扇的骨柄与团扇的直径一样长，折扇扇面的宽度是骨柄长的一半，折扇张开的角度为120 °，问哪一把扇子扇面的面积大？
【活动4】
例4.多少我国著名的引水工程的主干线输水管的直径为2.5m,设计流量为.如果水管截面中水面面积如图所示,其中∠AOB=45°,那么水的流速因达到.
二、巩固练习
1.已知扇形的半径为3cm，圆心角为120°，则扇形的面积为 __________cm2（结果保留π）.
2.设计一个商标图案（如图所示），在△ABC中，AB=AC=2cm , ∠B=30°，以A为圆心，AB为半径, 以BC为直径作半圆.求商标图案(即阴影部分)的面积.
三、当堂检测
1、已知圆的半径为18cm，扇形的圆心角为。求扇形的面积。
2、一扇形的半径等于已知圆的半径的2倍，且它的面积等于该已知圆的面积。求这一扇形的圆心角。
3、已知一个扇形的面积是，圆心角是，求它的弧长。
4、如图，水平放置的圆柱形排水管的截面半径为12cm，截面中有水部分弓形的高为6cm。求截面中有水部分弓形面积（精确到）
5.如图，在矩形ABCD中，AD=2AB=2，以B为圆心，以AB为半径作圆弧，交CB的延长线于点E，连结DE。求图中阴影分布的面积。
6.如图，扇形AOB的圆心角为直角，边长为1的正方形OCDE的顶点C,E,D分别在OA,OB,弧AB上。过点A作AF⊥ED,交ED的延长线于点F。求图中阴影部分的面积。
四、反思归纳
1、本节课学习的内容：
2、数学思想方法归纳：
B
A
O
O