1.1 二次根式

第1章 二次根式
1.1 二次根式
班级 姓名
学习目标：
1.经历二次根式概念的发生过程。
2.了解二次根式的概念。
3.理解二次根式何时有意义，何时无意义，会在简单情况下求根号内所有含字母的取值范围。
4.会求二次根式的值。
学习重点： 二次根式的概念
学习难点：例1的第（2）（3）题学生不容易理解
一、预习：
1.什么叫平方根? ____________________________________________
2.什么叫算术平方根? ____________________________________________
3. 计算:
(1)的平方根是 ；
(2)如图,在RABC中,AB=50m,BC=m,则AC= m；
(3)圆的面积为S,则圆的半径是 ；
(4)正方形的面积为,则边长为 。
对上面（2）~（4）题的结果,你能发现它们有什么共同的特征吗?
4. 阅读教科书中的本节内容后回答：
要使形如算术平方根（二次根式）的代数式有意义，则x的取值范围是 .要使二次根式有意义，必须满足条件 .
例1（2）中为什么被开方式>0而不是，请你说出理由；
例1（3）中为什么无论a取何值，都有，请你说出理由.
5、预习后，你或许有些疑问，请写在下面的空白处：
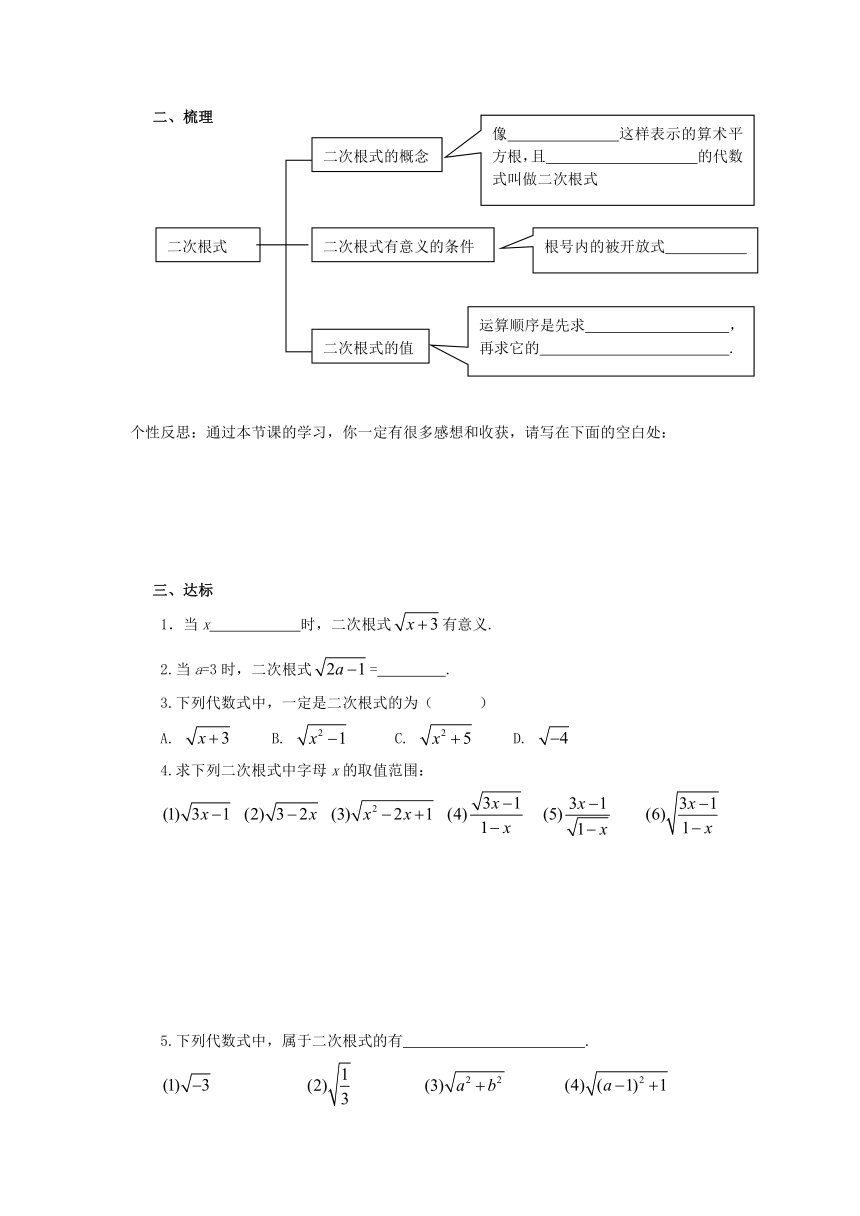
二、梳理
个性反思：通过本节课的学习，你一定有很多感想和收获，请写在下面的空白处：
三、达标
1．当x 时，二次根式有意义.
2.当a=3时，二次根式= .
3.下列代数式中，一定是二次根式的为（ ）
A. B. C. D.
4.求下列二次根式中字母x的取值范围：

5.下列代数式中，属于二次根式的有 .


6.二次根式的最小值是 ，此时x的值为 ,
当x为 时，代数式有最 (填小或大)值是 .
7.若二次根式有意义，化简
8.当x = -4 时，求二次根式 的值
9、若二次根式 的值为3，求x的值.
四、挑战
1．已知，求代数式的值.
2.已知m,n都是实数，且满足，求的值.
五、攀登
已知，求的值.