切线及其应用[上学期]
图片预览


文档简介
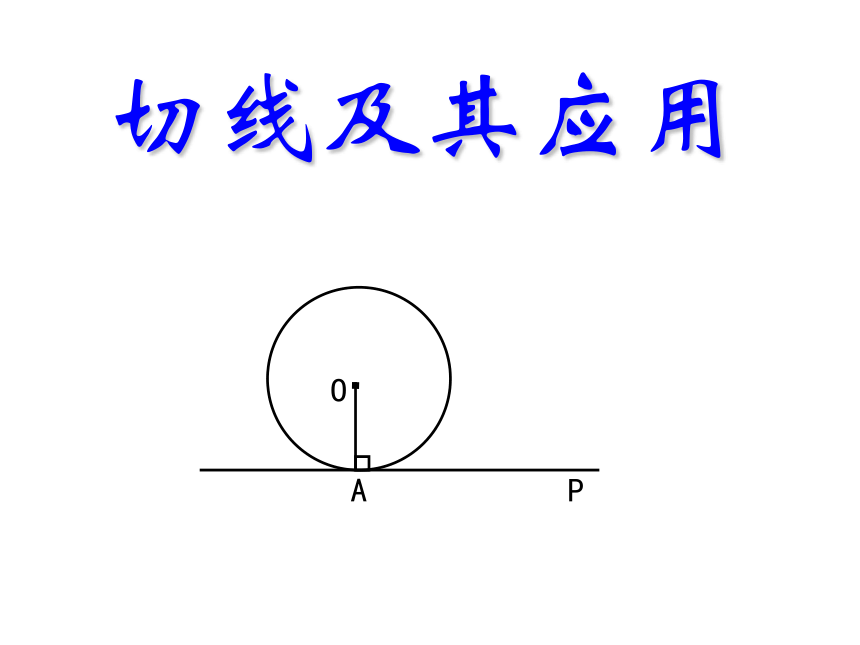
课件21张PPT。切线及其应用直线与圆位置关系之二:切线及其应用AP切线及其应用问题1:
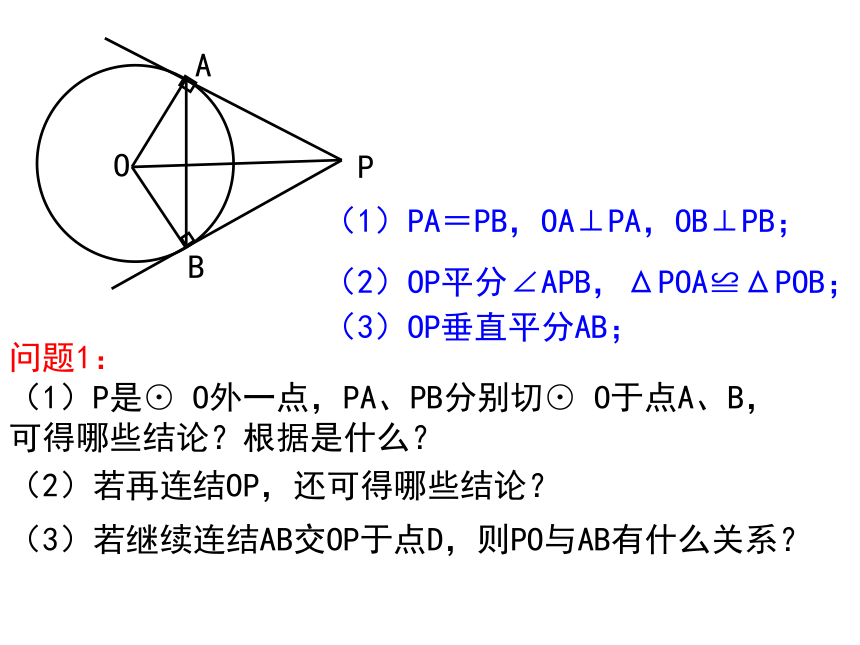
(1)P是⊙ O外一点,PA、PB分别切⊙ O于点A、B,
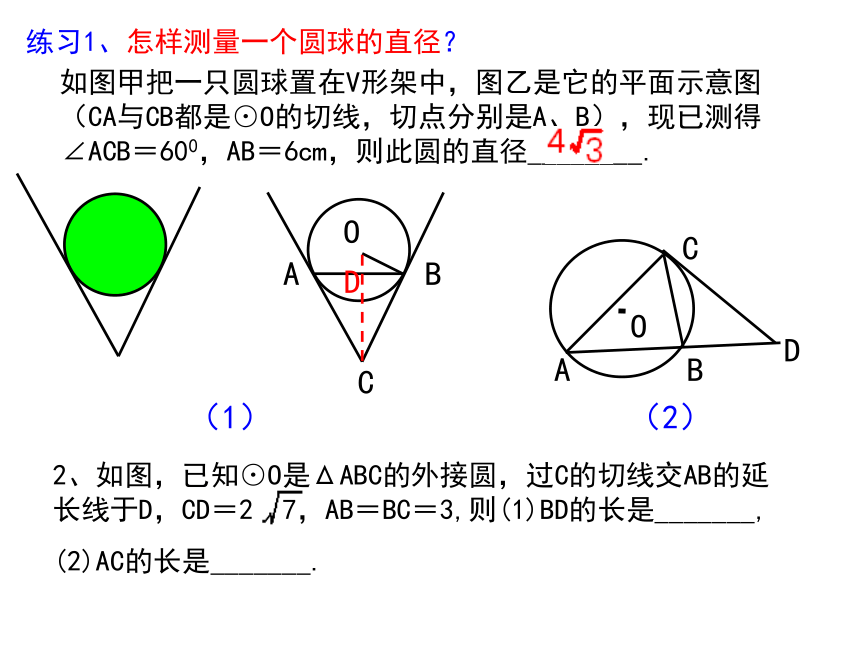
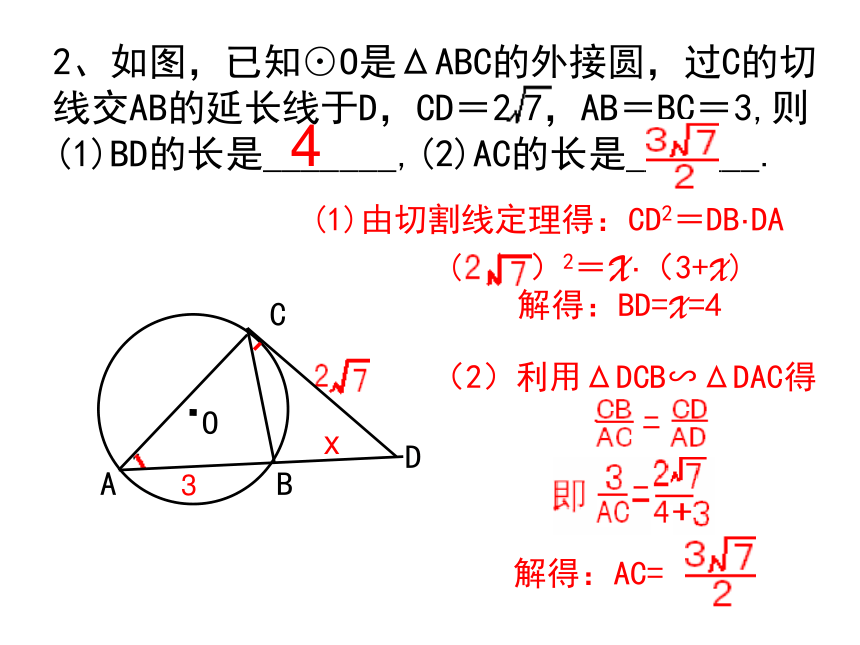
可得哪些结论?根据是什么?(1)PA=PB,OA⊥PA,OB⊥PB;(2)若再连结OP,还可得哪些结论?(2)OP平分∠APB,ΔPOA≌ΔPOB;(3)若继续连结AB交OP于点D,则PO与AB有什么关系?(3)OP垂直平分AB;如图甲把一只圆球置在V形架中,图乙是它的平面示意图(CA与CB都是⊙O的切线,切点分别是A、B),现已测得∠ACB=600,AB=6cm,则此圆的直径________.练习1、怎样测量一个圆球的直径?(1)(2)(2)利用ΔDCB∽ΔDAC得4(1)由切割线定理得:CD2=DB·DA解得:BD=X=4OABP问题2:
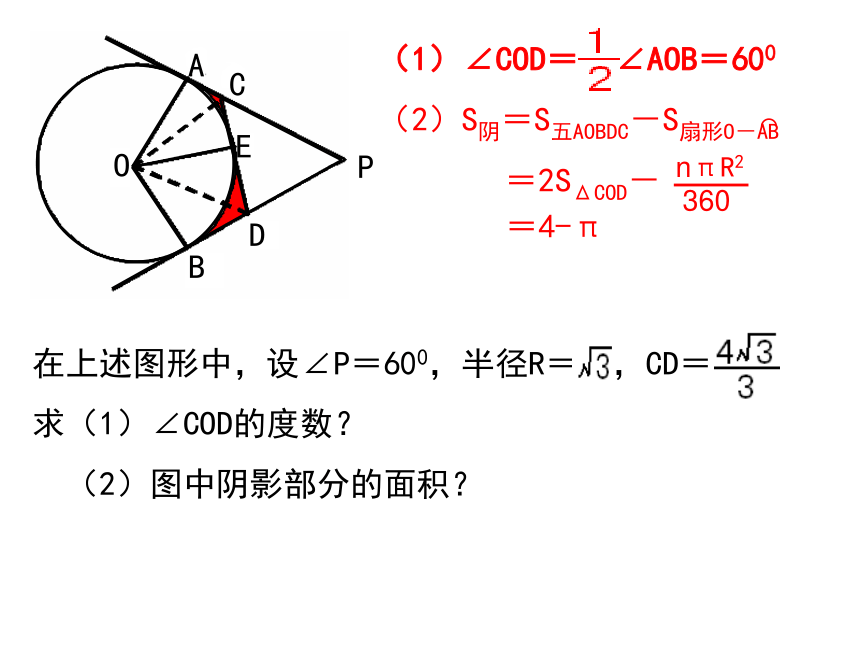
(1)在问题1的基础上,再添上CD切⊙O于E,并分别交PA、PB于点C、D,又可得出哪些结论?(1)ΔCDP的周长=PA+PB
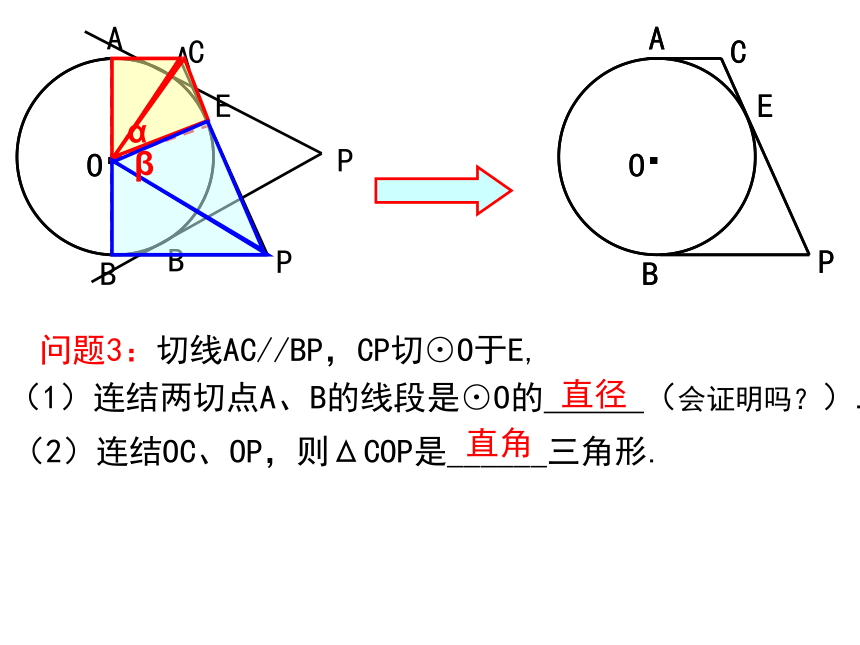
=2PA=2PB;(2)若连结OA、OB、OE,则可得什么结论呢?(2)OA⊥PA,OB⊥PB,OE⊥CD;(3)若再连结OC、OD呢?(3)ΔAOC≌ΔCOE,ΔBOD≌ΔDOE;(4)五边形AOBDC的面积与ΔCOD的面积有什么关系?(4)S五AOBDC=2SΔCOD;OABEDCP =4-π问题3:切线AC//BP,CP切⊙O于E,(1)连结两切点A、B的线段是⊙O的 (会证明吗?).(2)连结OC、OP,则ΔCOP是______三角形.直径直角例:已知如图:正方形ABPF的边长为4,以AB为直径画⊙O,CP切⊙O于E,交AF于C
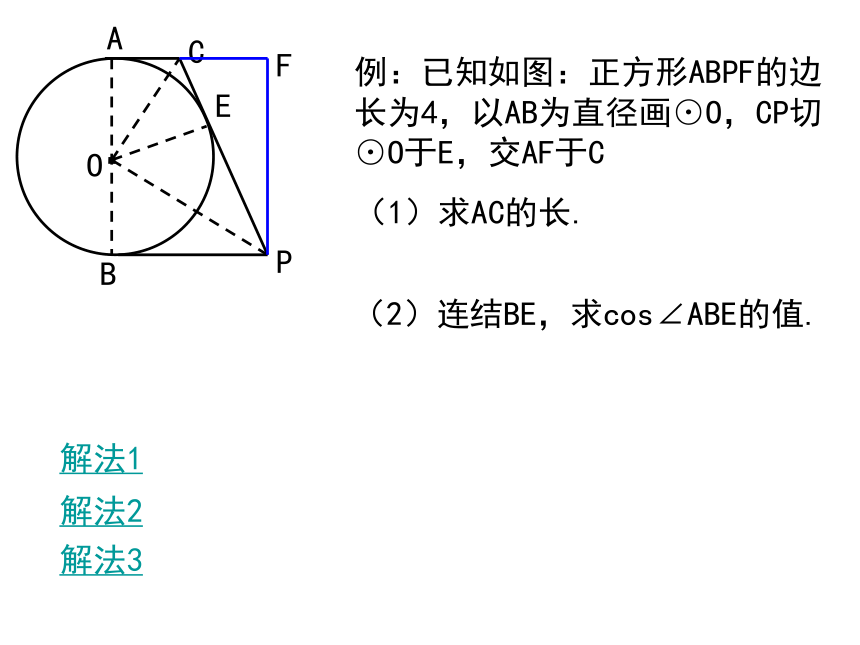
(1)求AC的长.解法3解法1解法2(2)连结BE,求cos∠ABE的值.解法3解法1解法2例:已知如图:正方形ABPF的边长为4,以AB为直径画⊙O,CP切⊙O于E,交AF于C
(1)求AC的长.(2)连结BE,求cos∠ABE的值.解法3解法1解法2(2)连结BE,求cos∠ABE的值.E例:已知如图:正方形ABPF的边长为4,以AB为直径画⊙O,CP切⊙O于E,交AF于C
(1)求AC的长.例:如图正方形ABCD中,有一以CB为直径的半圆,BC=2cm,现有两点E、F分别从点B、点A同时出发,点E沿线段BA以1cm/s的速度向点A运动,点F沿折线A-D-C以2cm/s的速度向点C运动,设点E离开点B的时间t秒(t≤2).(1)t为何值时,线段EF与BC平行?并在图中画出EF.解:设E、F出发后t秒时,EF//BC,
则BE=CF,∵BE=t,CF=4-2t∴t=4-2t ∴t=4/3∴当t=4/3时,EF//BC(2)设1(2)若∠C=300,可得哪些线段相等,PC与PB有什么数量关系?
(3)∠C可能等于450吗?若∠C= 450 则过点A的切线与CB有怎样的位置关系?在图乙中画出图形.
(4)若∠C>450,则过点A的切线与直线CB的交点P的位置将在哪里?在图丙中画出图形.甲乙丙2∠BAP+∠P=900BA=BP,AC=APPC=3PBA平行 APAOPBCF解法1:利用相似,即ΔAOC∽ΔBOPAOPBCEF224x解法2:利用射影定理,即OE2=CE·PEAOPBCEF4x4xG4-xx解法3:作CG⊥PB于G,利用勾股定理,结合方程思想可得,即CG2+PG2=CP2
(1)P是⊙ O外一点,PA、PB分别切⊙ O于点A、B,
可得哪些结论?根据是什么?(1)PA=PB,OA⊥PA,OB⊥PB;(2)若再连结OP,还可得哪些结论?(2)OP平分∠APB,ΔPOA≌ΔPOB;(3)若继续连结AB交OP于点D,则PO与AB有什么关系?(3)OP垂直平分AB;如图甲把一只圆球置在V形架中,图乙是它的平面示意图(CA与CB都是⊙O的切线,切点分别是A、B),现已测得∠ACB=600,AB=6cm,则此圆的直径________.练习1、怎样测量一个圆球的直径?(1)(2)(2)利用ΔDCB∽ΔDAC得4(1)由切割线定理得:CD2=DB·DA解得:BD=X=4OABP问题2:
(1)在问题1的基础上,再添上CD切⊙O于E,并分别交PA、PB于点C、D,又可得出哪些结论?(1)ΔCDP的周长=PA+PB
=2PA=2PB;(2)若连结OA、OB、OE,则可得什么结论呢?(2)OA⊥PA,OB⊥PB,OE⊥CD;(3)若再连结OC、OD呢?(3)ΔAOC≌ΔCOE,ΔBOD≌ΔDOE;(4)五边形AOBDC的面积与ΔCOD的面积有什么关系?(4)S五AOBDC=2SΔCOD;OABEDCP =4-π问题3:切线AC//BP,CP切⊙O于E,(1)连结两切点A、B的线段是⊙O的 (会证明吗?).(2)连结OC、OP,则ΔCOP是______三角形.直径直角例:已知如图:正方形ABPF的边长为4,以AB为直径画⊙O,CP切⊙O于E,交AF于C
(1)求AC的长.解法3解法1解法2(2)连结BE,求cos∠ABE的值.解法3解法1解法2例:已知如图:正方形ABPF的边长为4,以AB为直径画⊙O,CP切⊙O于E,交AF于C
(1)求AC的长.(2)连结BE,求cos∠ABE的值.解法3解法1解法2(2)连结BE,求cos∠ABE的值.E例:已知如图:正方形ABPF的边长为4,以AB为直径画⊙O,CP切⊙O于E,交AF于C
(1)求AC的长.例:如图正方形ABCD中,有一以CB为直径的半圆,BC=2cm,现有两点E、F分别从点B、点A同时出发,点E沿线段BA以1cm/s的速度向点A运动,点F沿折线A-D-C以2cm/s的速度向点C运动,设点E离开点B的时间t秒(t≤2).(1)t为何值时,线段EF与BC平行?并在图中画出EF.解:设E、F出发后t秒时,EF//BC,
则BE=CF,∵BE=t,CF=4-2t∴t=4-2t ∴t=4/3∴当t=4/3时,EF//BC(2)设1
(3)∠C可能等于450吗?若∠C= 450 则过点A的切线与CB有怎样的位置关系?在图乙中画出图形.
(4)若∠C>450,则过点A的切线与直线CB的交点P的位置将在哪里?在图丙中画出图形.甲乙丙2∠BAP+∠P=900BA=BP,AC=APPC=3PBA平行 APAOPBCF解法1:利用相似,即ΔAOC∽ΔBOPAOPBCEF224x解法2:利用射影定理,即OE2=CE·PEAOPBCEF4x4xG4-xx解法3:作CG⊥PB于G,利用勾股定理,结合方程思想可得,即CG2+PG2=CP2
