弧长与扇形的面积[上学期]

课件20张PPT。弧长与扇形的面积弧长1．已知⊙O半径为R，⊙O的周长C是多大？
2．已知⊙O的周长是C，⊙O的半径R等于多少
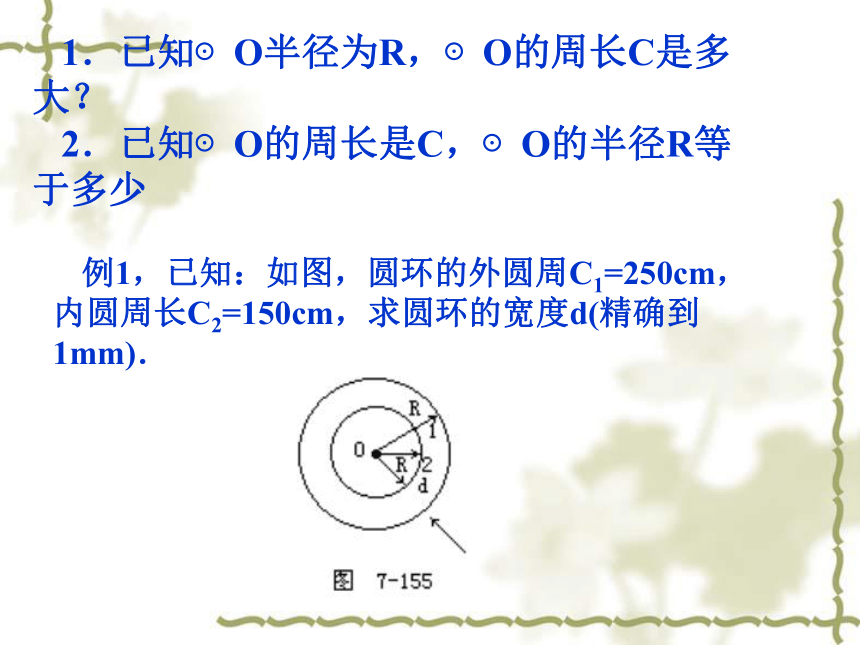
例1，已知：如图，圆环的外圆周C1=250cm，内圆周长C2=150cm，求圆环的宽度d(精确到1mm)．
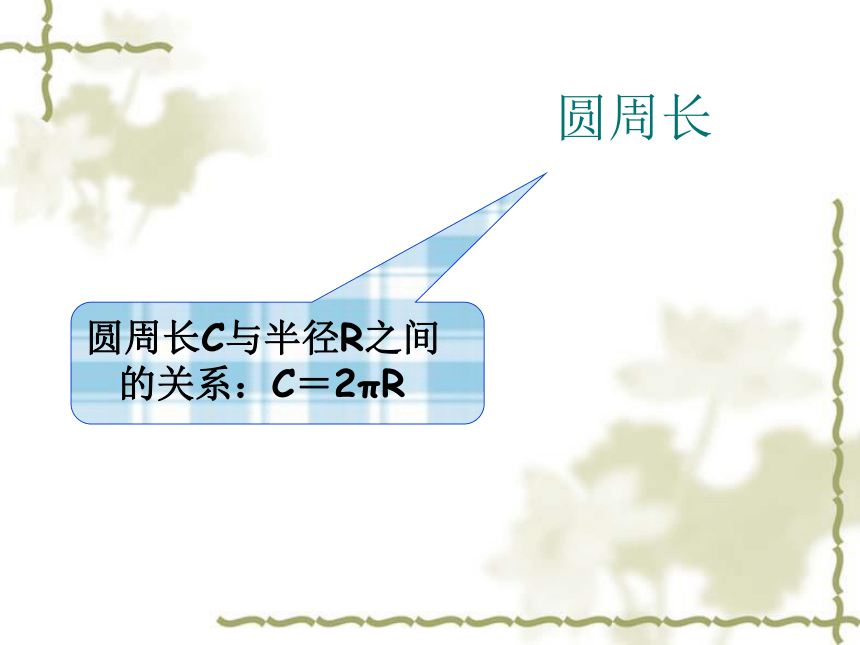
圆周长圆周长C与半径R之间的关系：C＝2πR我们知道，把顶点在圆心的周角等分成360份时，每一份的圆心角是1°的角，因为同圆中相等的圆心角所对弧相等，所以整个圆也被等分成360份，每一份这样的弧就是1°的弧，大家知道圆的周长是2πR，想想看1°的弧长应是多少？怎样求？ n°的弧长应是多少？ 想一想n°的圆心角所对的弧长=nπR／180
1°的圆心角所对的弧长=πR／180弧长计算公式公式中n和180都不要带单位“度”
圆心角的单位必须化为“度”
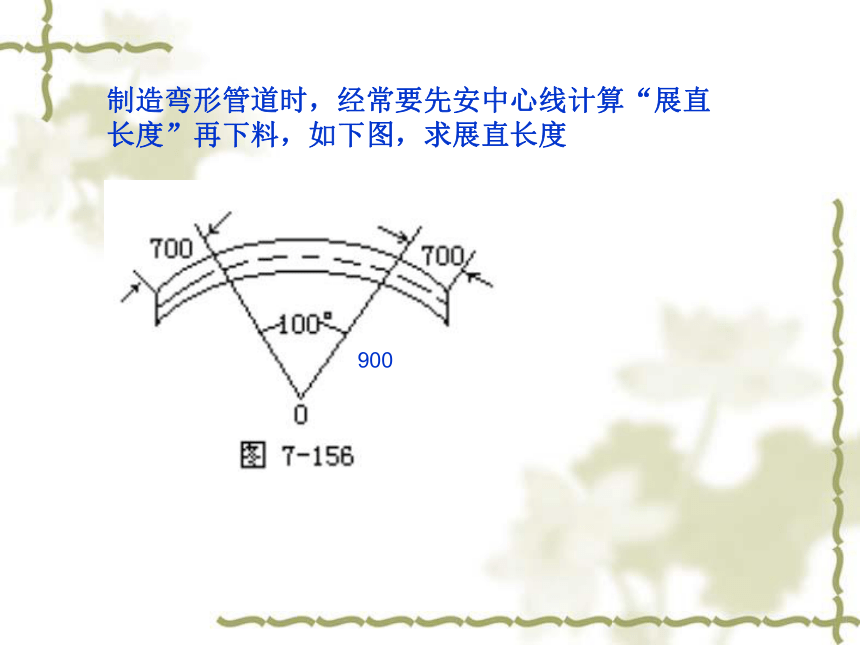
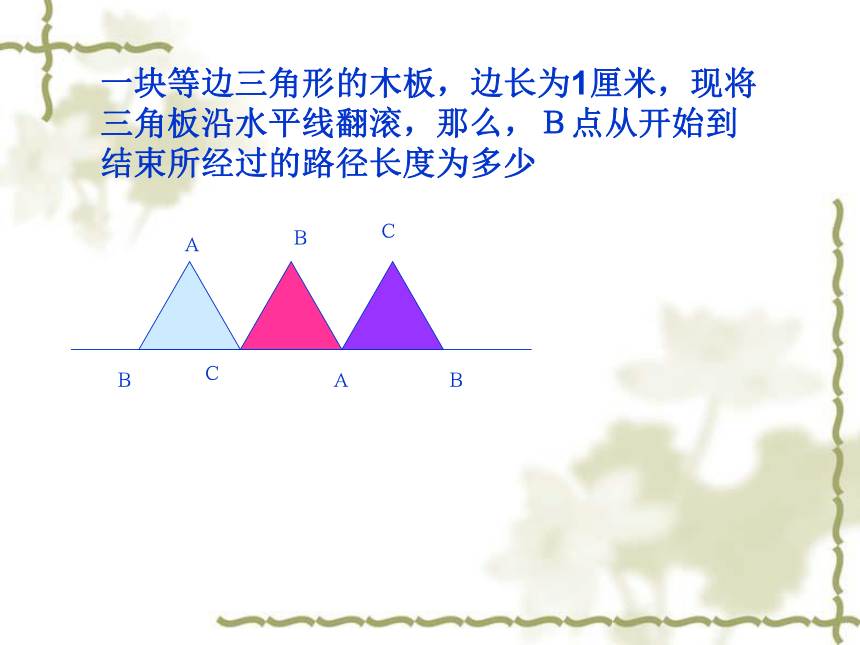
题中没有标明精确度，结果用π表示制造弯形管道时，经常要先安中心线计算“展直长度”再下料，如下图，求展直长度900一块等边三角形的木板，边长为1厘米，现将三角板沿水平线翻滚，那么，Ｂ点从开始到结束所经过的路径长度为多少ＡＢＣＢＡＣＢ扇形的面积若将360°的圆心角360等分，就得到了360等份的弧．在这个过程中不难发现圆周被分割成360等份的同时，面积也被分割成360等份，于是就要研究这每一份的面积，
πR2/360
1°的圆心角所对的面积=n°的圆心角所对的面积=nπR2/360
它们有什么特点由圆心角的两条半径和圆心角所对的弧所围成的图形，我们称之为扇形．
1°的圆心角所对的扇形面积=πR2/360
n°的圆心角所对的扇形面积=nπR2/360
扇形 习题课小结一、弧长的计算公式二、扇形面积计算公式S扇=____．
弓形面积弓形：由弦及其所对的弧组成的图形弓形面积S弓形=
S扇形-S△AOBS弓形=
S扇形+S△AOBS弓形=S半圆如图，水平放置的圆柱形水管道的截面半径是0.6米，其中水面高0.3米。求截面有水部分的面积（精确到0.01平方米）OABDC已知正三角形的边长为a，求它的内切圆与外接圆组成的圆环的面积。圆环面积把上题中的正三角形改为正方形，结果会怎样？
猜想：正五边形、正六边形时又会怎样？
用文字表达你得到的结论。求不规则图形面积时，要认真观察图形，准确分解与组合，化归为常见的基本图形。