1.1锐角三角函数(1)[下学期]
图片预览

文档简介
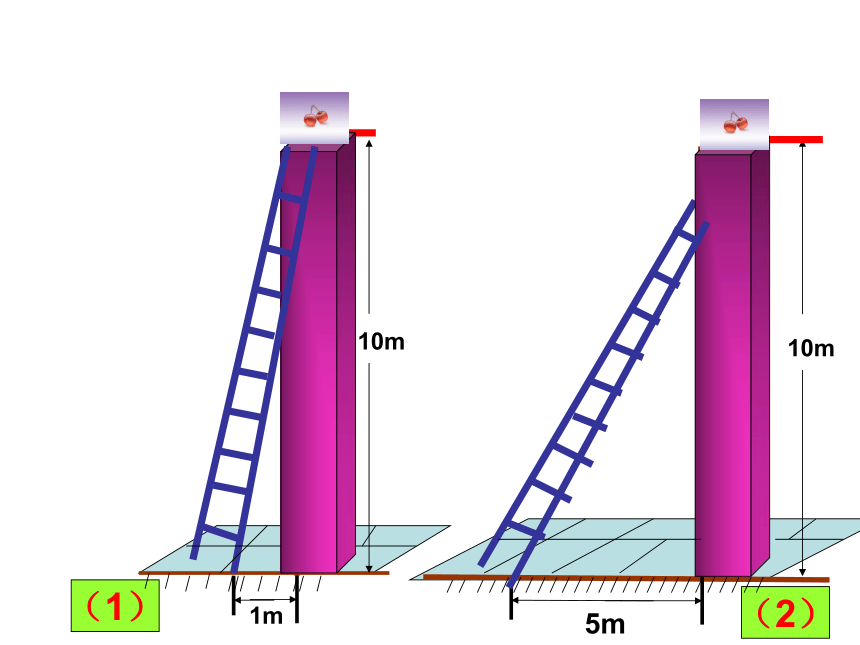
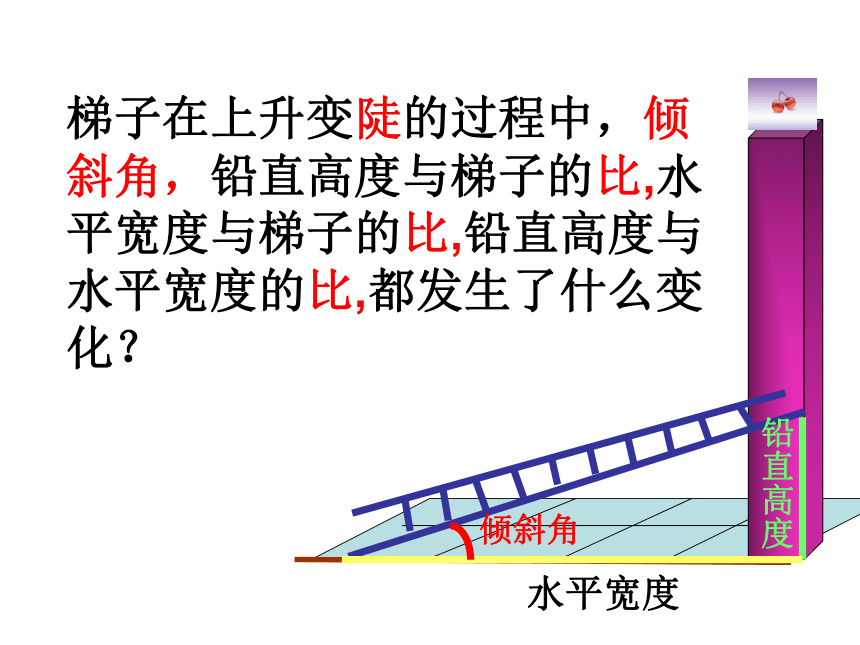
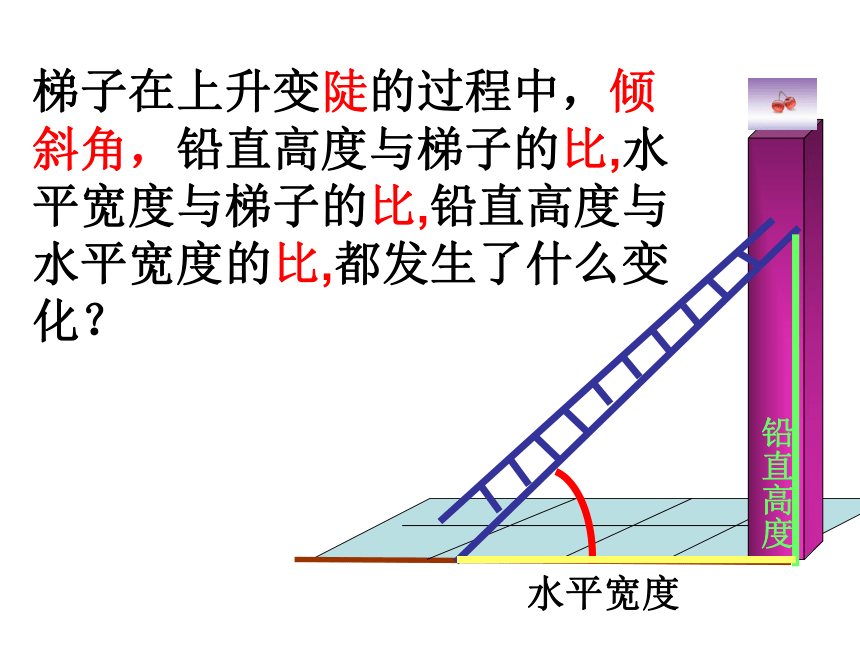
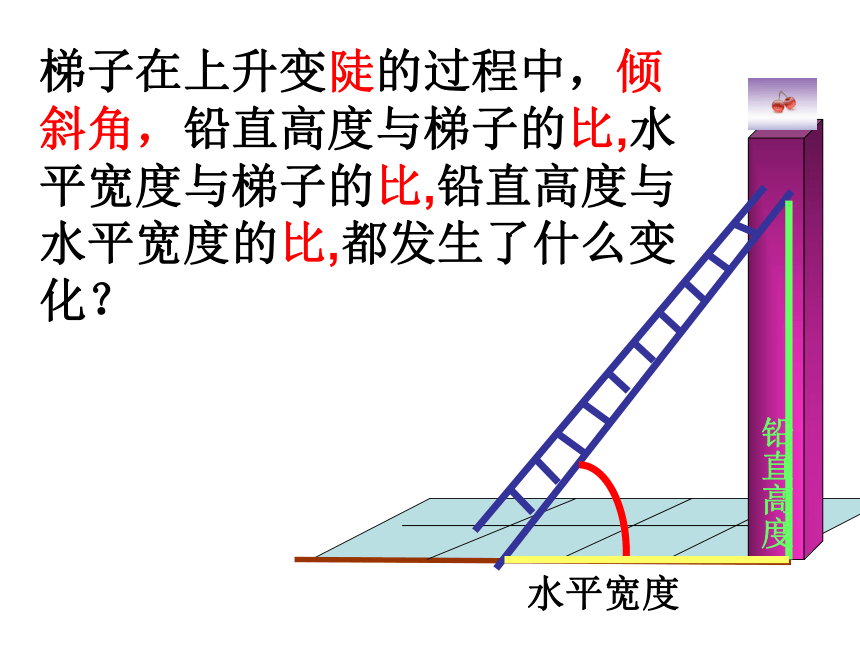
课件27张PPT。1.1锐角三角函数(1)虹桥镇二中数学组制作10m1m 5m10m(1)(2)梯子在上升变陡的过程中,倾斜角,铅直高度与梯子的比,水平宽度与梯子的比,铅直高度与水平宽度的比,都发生了什么变化? 水平宽度铅直高度倾斜角铅直高度水平宽度梯子在上升变陡的过程中,倾斜角,铅直高度与梯子的比,水平宽度与梯子的比,铅直高度与水平宽度的比,都发生了什么变化?
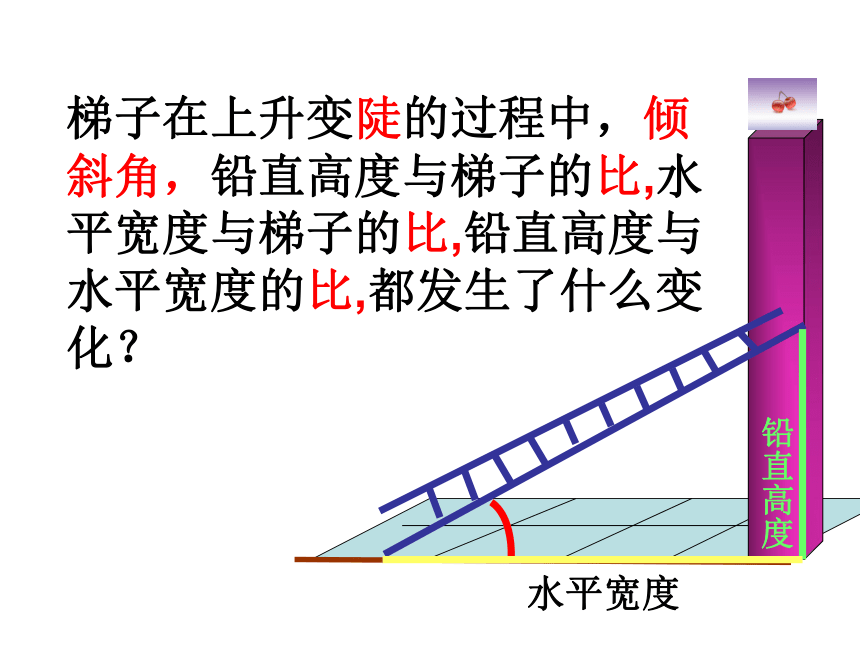
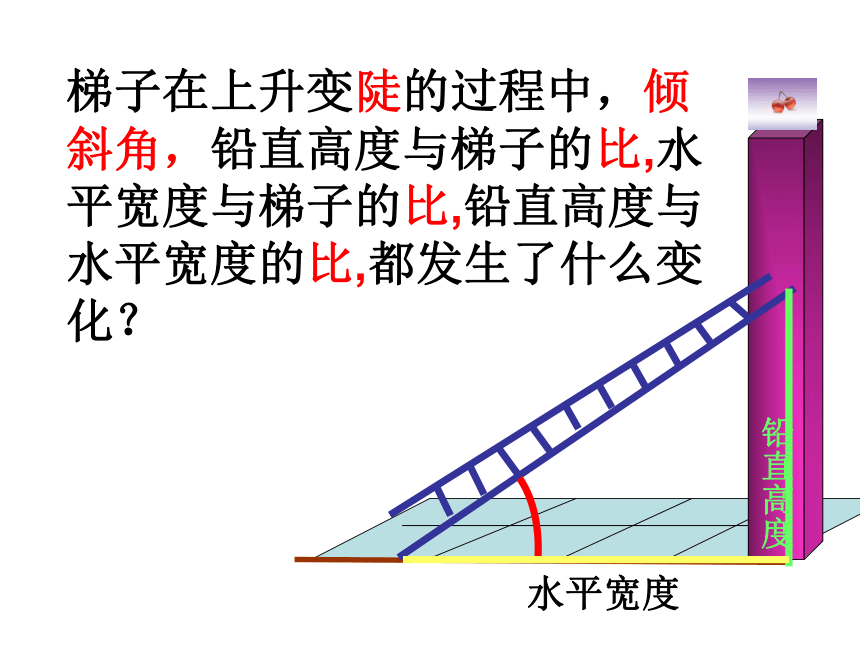
铅直高度水平宽度梯子在上升变陡的过程中,倾斜角,铅直高度与梯子的比,水平宽度与梯子的比,铅直高度与水平宽度的比,都发生了什么变化? 铅直高度水平宽度梯子在上升变陡的过程中,倾斜角,铅直高度与梯子的比,水平宽度与梯子的比,铅直高度与水平宽度的比,都发生了什么变化? 铅直高度水平宽度梯子在上升变陡的过程中,倾斜角,铅直高度与梯子的比,水平宽度与梯子的比,铅直高度与水平宽度的比,都发生了什么变化?
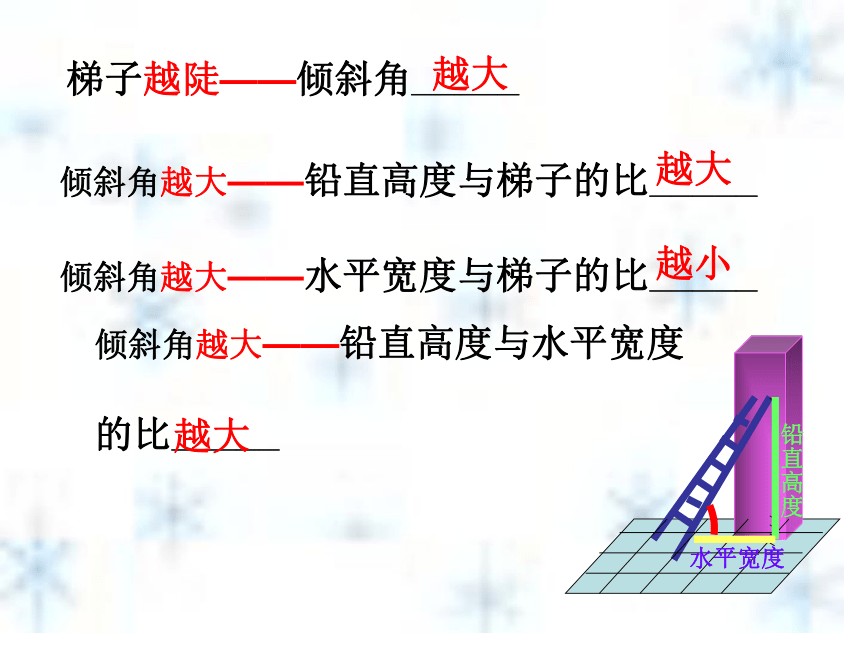
梯子越陡——倾斜角_____倾斜角越大——铅直高度与梯子的比_____倾斜角越大——水平宽度与梯子的比_____倾斜角越大——铅直高度与水平宽度
的比_____
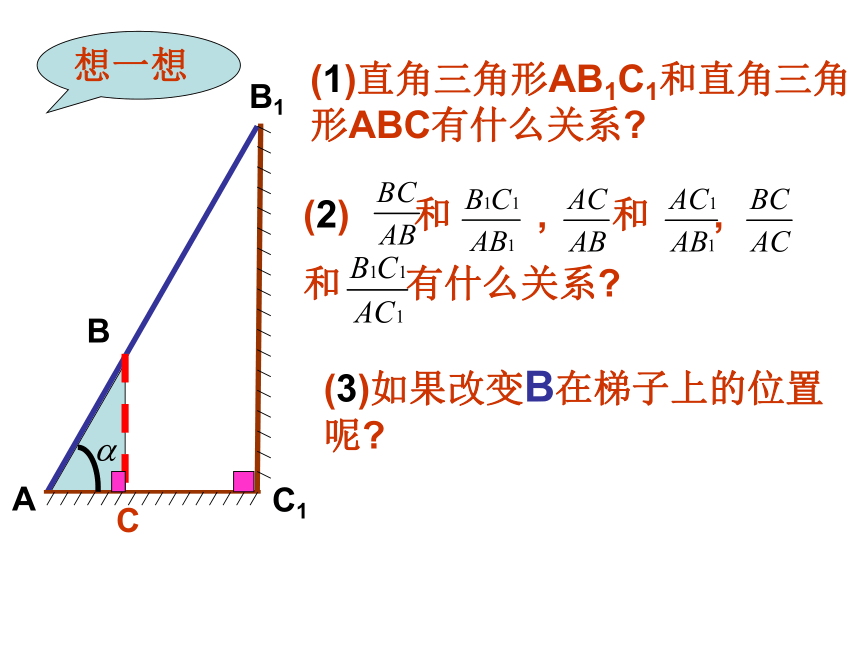
铅直高度水平宽度越大越大越小越大 AB1 C1 CB想一想(1)直角三角形AB1C1和直角三角 形ABC有什么关系?(2) 和 , 和 ,
和 有什么关系? (3)如果改变B在梯子上的位置呢? AB1 C1 CB想一想(1)直角三角形AB1C1和直角三角 形ABC有什么关系?(2) 和 , 和 ,
和 有什么关系?(3)如果改变B在梯子上的位置呢? AB1 C1 CB想一想(1)直角三角形AB1C1和直角三角 形ABC有什么关系?(2) 和 , 和 ,
和 有什么关系?(3)如果改变B在梯子上的位置呢? AB1 C1 CB想一想(1)直角三角形AB1C1和直角三角 形ABC有什么关系?(2) 和 , 和 ,
和 有什么关系?(3)如果改变B在梯子上的位置呢? AB1 C1 CB想一想(1)直角三角形AB1C1和直角三角 形ABC有什么关系?(2) 和 , 和 ,
和 有什么关系?(3)如果改变B在梯子上的位置呢? AB C∠A的对边∠A的邻边∠A的对边∠A的邻边tanAcosA∠A的邻边∠A的对边斜边sinA斜边斜边1。锐角α的正弦、余弦、和正切统称∠α的三角函数2。锐角的三角函数的值都是正实数,并且0〈sin α〈1,0〈cosα〈1 ,定义注意:三角函数的定义,必须在直角三角形中. AB C例1 如图,在Rt△ABC中,∠C=90°
AB=5,BC=3, 求∠A, ∠B的正弦,
余弦和正切. 若AC=5,BC=3呢?观察以上计算结果,你发现了什么?
例2 如图:在Rt△ABC中,∠B=900,AC=200,sinA=0.6.
求:BC的长.1.如图:在等腰△ABC中,AB=AC=5,BC=6.
求: sinB,cosB,tanB.
求:△ABC的周长.老师提示:过点A作AD垂直于BC于D.练习3.如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,sinA的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定4.已知∠A,∠B为锐角
(1)若∠A=∠B,则sinA sinB;
(2)若sinA=sinB,则∠A ∠B.练习5.如图, ∠C=90°CD⊥AB.6.在上图中,若BD=6,CD=12.求cosA的值.练习7.如图,分别根据图(1)和图(2)求∠A的三个三角函数值.8.在Rt△ABC中,∠C=90°, (1)AC=3,AB=6,求sinA和cosB
(2)BC=3,sinA= ,求AC和AB.老师提示:
求锐角三角函数时,勾股定理的运用是很重要的.练习谈谈今天的收获畅所欲言 AB C∠A的对边∠A的邻边∠A的对边∠A的邻边tanAcosA∠A的邻边∠A的对边斜边sinA斜边斜边定义回味无穷定义中应该注意的几个问题:1.sinA,cosA,tanA, 是在直角三角形中定义的, ∠A是锐角(注意数形结合,构造直角三角形).
2.sinA,cosA,tanA, 是一个完整的符号,表示∠A
的正切,习惯省去“∠”号;
3.sinA,cosA,tanA, 是一个比值.注意比的顺序,
且sinA,cosA,tanA, 均﹥0,无单位.
4.sinA,cosA,tanA, 的大小只与∠A的大小有关,
而与直角三角形的边长无关.
5.角相等,则其三角函数值相等;两锐角的三角函数值相等,则这两个锐角相等.10m1m 5m10m(1)(2)1.书本作业题第6题
2.同步练习在直角三角形中,若一个锐角确定,那么这个角的对边,邻边和斜边之间的比值也随之确定.直角三角形中边与角的关系:锐角三角函数.sinA和cosB,tanA和cotB有什么关系?sinA=cosB,tanA=cotB.下课了!
铅直高度水平宽度梯子在上升变陡的过程中,倾斜角,铅直高度与梯子的比,水平宽度与梯子的比,铅直高度与水平宽度的比,都发生了什么变化? 铅直高度水平宽度梯子在上升变陡的过程中,倾斜角,铅直高度与梯子的比,水平宽度与梯子的比,铅直高度与水平宽度的比,都发生了什么变化? 铅直高度水平宽度梯子在上升变陡的过程中,倾斜角,铅直高度与梯子的比,水平宽度与梯子的比,铅直高度与水平宽度的比,都发生了什么变化?
梯子越陡——倾斜角_____倾斜角越大——铅直高度与梯子的比_____倾斜角越大——水平宽度与梯子的比_____倾斜角越大——铅直高度与水平宽度
的比_____
铅直高度水平宽度越大越大越小越大 AB1 C1 CB想一想(1)直角三角形AB1C1和直角三角 形ABC有什么关系?(2) 和 , 和 ,
和 有什么关系? (3)如果改变B在梯子上的位置呢? AB1 C1 CB想一想(1)直角三角形AB1C1和直角三角 形ABC有什么关系?(2) 和 , 和 ,
和 有什么关系?(3)如果改变B在梯子上的位置呢? AB1 C1 CB想一想(1)直角三角形AB1C1和直角三角 形ABC有什么关系?(2) 和 , 和 ,
和 有什么关系?(3)如果改变B在梯子上的位置呢? AB1 C1 CB想一想(1)直角三角形AB1C1和直角三角 形ABC有什么关系?(2) 和 , 和 ,
和 有什么关系?(3)如果改变B在梯子上的位置呢? AB1 C1 CB想一想(1)直角三角形AB1C1和直角三角 形ABC有什么关系?(2) 和 , 和 ,
和 有什么关系?(3)如果改变B在梯子上的位置呢? AB C∠A的对边∠A的邻边∠A的对边∠A的邻边tanAcosA∠A的邻边∠A的对边斜边sinA斜边斜边1。锐角α的正弦、余弦、和正切统称∠α的三角函数2。锐角的三角函数的值都是正实数,并且0〈sin α〈1,0〈cosα〈1 ,定义注意:三角函数的定义,必须在直角三角形中. AB C例1 如图,在Rt△ABC中,∠C=90°
AB=5,BC=3, 求∠A, ∠B的正弦,
余弦和正切. 若AC=5,BC=3呢?观察以上计算结果,你发现了什么?
例2 如图:在Rt△ABC中,∠B=900,AC=200,sinA=0.6.
求:BC的长.1.如图:在等腰△ABC中,AB=AC=5,BC=6.
求: sinB,cosB,tanB.
求:△ABC的周长.老师提示:过点A作AD垂直于BC于D.练习3.如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,sinA的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定4.已知∠A,∠B为锐角
(1)若∠A=∠B,则sinA sinB;
(2)若sinA=sinB,则∠A ∠B.练习5.如图, ∠C=90°CD⊥AB.6.在上图中,若BD=6,CD=12.求cosA的值.练习7.如图,分别根据图(1)和图(2)求∠A的三个三角函数值.8.在Rt△ABC中,∠C=90°, (1)AC=3,AB=6,求sinA和cosB
(2)BC=3,sinA= ,求AC和AB.老师提示:
求锐角三角函数时,勾股定理的运用是很重要的.练习谈谈今天的收获畅所欲言 AB C∠A的对边∠A的邻边∠A的对边∠A的邻边tanAcosA∠A的邻边∠A的对边斜边sinA斜边斜边定义回味无穷定义中应该注意的几个问题:1.sinA,cosA,tanA, 是在直角三角形中定义的, ∠A是锐角(注意数形结合,构造直角三角形).
2.sinA,cosA,tanA, 是一个完整的符号,表示∠A
的正切,习惯省去“∠”号;
3.sinA,cosA,tanA, 是一个比值.注意比的顺序,
且sinA,cosA,tanA, 均﹥0,无单位.
4.sinA,cosA,tanA, 的大小只与∠A的大小有关,
而与直角三角形的边长无关.
5.角相等,则其三角函数值相等;两锐角的三角函数值相等,则这两个锐角相等.10m1m 5m10m(1)(2)1.书本作业题第6题
2.同步练习在直角三角形中,若一个锐角确定,那么这个角的对边,邻边和斜边之间的比值也随之确定.直角三角形中边与角的关系:锐角三角函数.sinA和cosB,tanA和cotB有什么关系?sinA=cosB,tanA=cotB.下课了!
