3.1直线与圆的位置关系(1)[下学期]
文档属性
| 名称 | 3.1直线与圆的位置关系(1)[下学期] |
|
|
| 格式 | rar | ||
| 文件大小 | 50.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-05-24 23:28:00 | ||
图片预览


文档简介
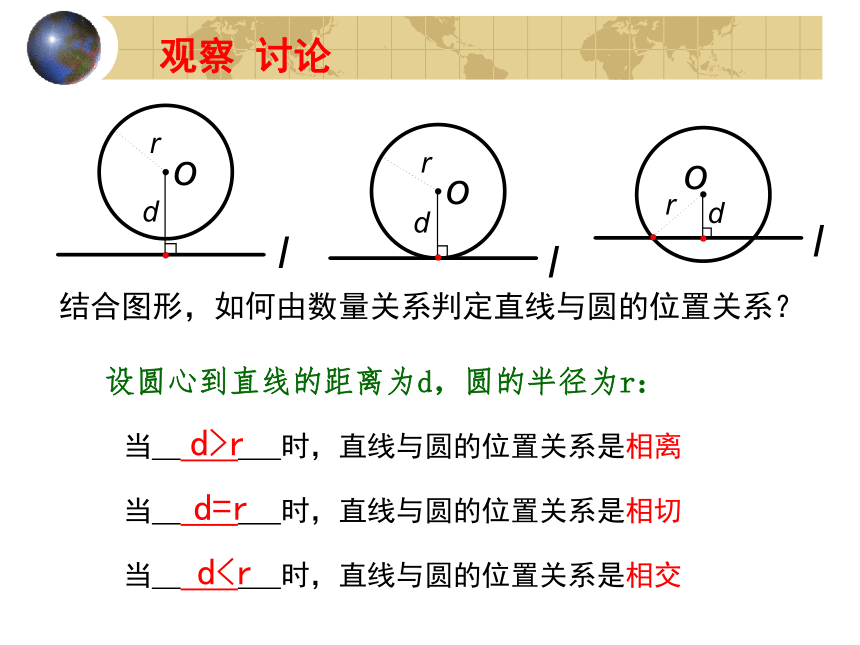
课件13张PPT。新浙教版九年级下册3.1
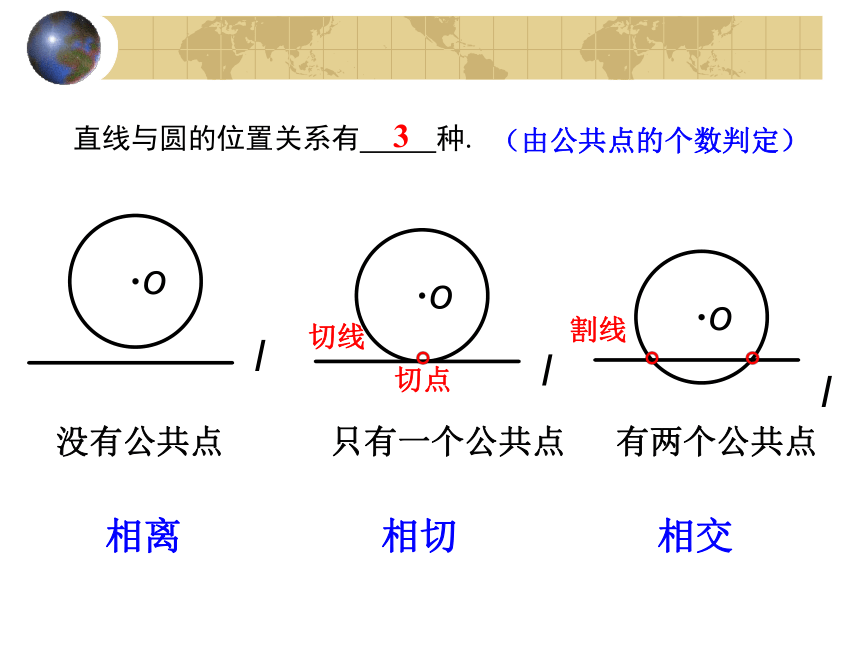
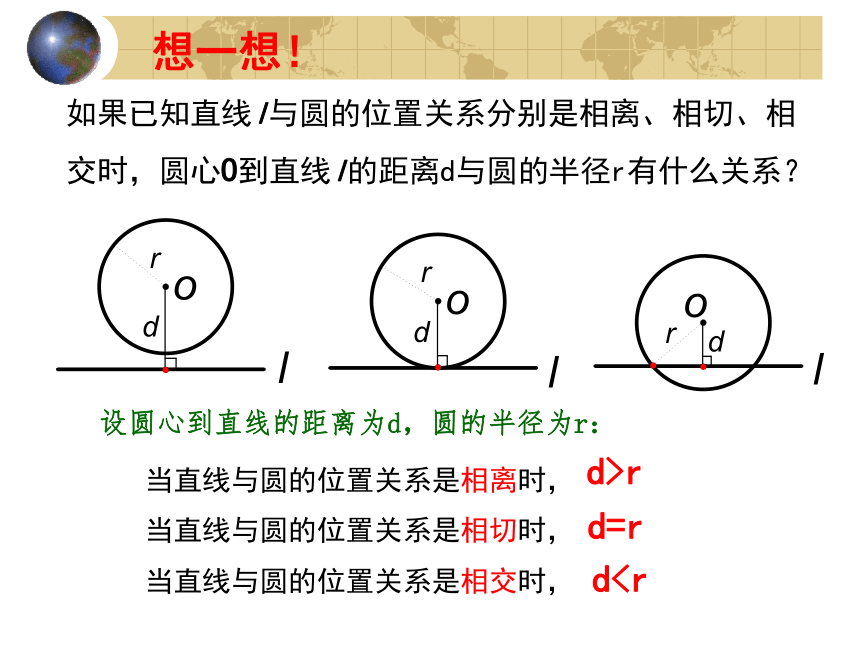
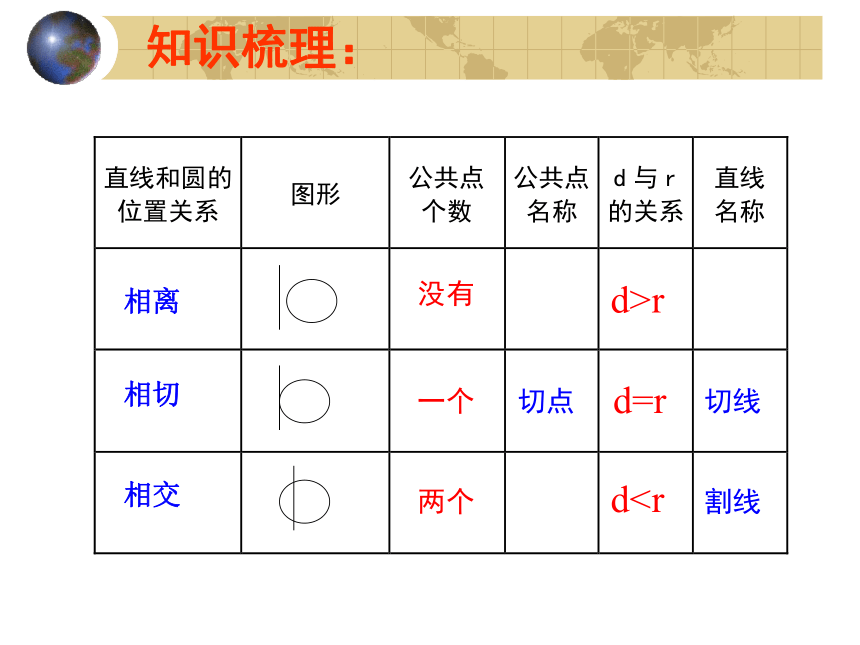
直线与圆的位置关系1看一看 想一想观察 讨论结合图形,如何由数量关系判定直线与圆的位置关系?d>rd=rd3没有公共点相离只有一个公共点相切切点切线有两个公共点相交割线(由公共点的个数判定)想一想!如果已知直线l与圆的位置关系分别是相离、相切、相交时,圆心O到直线l的距离d与圆的半径r有什么关系?当直线与圆的位置关系是相离时,当直线与圆的位置关系是相切时,当直线与圆的位置关系是相交时,d>rd=rdr d=r d为以下情况,那么圆的半径应分别取怎样的值?
(1)相交;(2)相切;(3)相离。练一练!1、已知圆的直径为13cm,如果直线和圆心的距离分别为
(1)d=4.5cm (2)d=6.5cm (3)d=8cm,
那么直线和圆有几个公共点?为什么?
例、在Rt△ABC中,∠C=900,AC=3cm,BC=4cm. (1)以A为圆心,3cm为半径的圆与直线BC的位置关系是 ;
以A为圆心,2cm为半径的圆与直线BC的位置关系是 ;
以A为圆心,3.5cm为半径的圆与直线BC的位置关系是 .(2)以C为圆心,半径r为何值时, ⊙C与
直线AB相切? 相离?相交?相切相交相离小结:说一说,这节课你有哪些收获?课后思考⑴垂直于半径的直线是圆的切线吗?⑵过半径外端的直线是圆的切线吗?⑶过半径的一端且垂直于半径的直线是圆的切线吗?⑷过半径外端且垂直于半径的直线是圆的切线吗?分层作业:1.基础题:作业本(2)P21;
2.自选题: 如图,一热带风暴中心O距A岛为2千米,风暴影响圈的半径为1千米.有一条船从A岛出发沿AB方向航行,问∠BAO的度数是多少时船就会进入风暴影响圈?再 见! 如图,在直角梯形ABCD中,∠B=90°,AD∥BC, ∠C= 30° ,AD=1,AB=2.
试猜想在BC是否存在一点P,使得⊙P与线段CD、
AB都相切,如存在,请确定⊙P的半径. 挑战自我!
直线与圆的位置关系1看一看 想一想观察 讨论结合图形,如何由数量关系判定直线与圆的位置关系?d>rd=rd
(1)相交;(2)相切;(3)相离。练一练!1、已知圆的直径为13cm,如果直线和圆心的距离分别为
(1)d=4.5cm (2)d=6.5cm (3)d=8cm,
那么直线和圆有几个公共点?为什么?
例、在Rt△ABC中,∠C=900,AC=3cm,BC=4cm. (1)以A为圆心,3cm为半径的圆与直线BC的位置关系是 ;
以A为圆心,2cm为半径的圆与直线BC的位置关系是 ;
以A为圆心,3.5cm为半径的圆与直线BC的位置关系是 .(2)以C为圆心,半径r为何值时, ⊙C与
直线AB相切? 相离?相交?相切相交相离小结:说一说,这节课你有哪些收获?课后思考⑴垂直于半径的直线是圆的切线吗?⑵过半径外端的直线是圆的切线吗?⑶过半径的一端且垂直于半径的直线是圆的切线吗?⑷过半径外端且垂直于半径的直线是圆的切线吗?分层作业:1.基础题:作业本(2)P21;
2.自选题: 如图,一热带风暴中心O距A岛为2千米,风暴影响圈的半径为1千米.有一条船从A岛出发沿AB方向航行,问∠BAO的度数是多少时船就会进入风暴影响圈?再 见! 如图,在直角梯形ABCD中,∠B=90°,AD∥BC, ∠C= 30° ,AD=1,AB=2.
试猜想在BC是否存在一点P,使得⊙P与线段CD、
AB都相切,如存在,请确定⊙P的半径. 挑战自我!
