1.3有关直角三角形的计算[下学期]
图片预览



文档简介
课件16张PPT。 解直角三角形(二)勾股定理
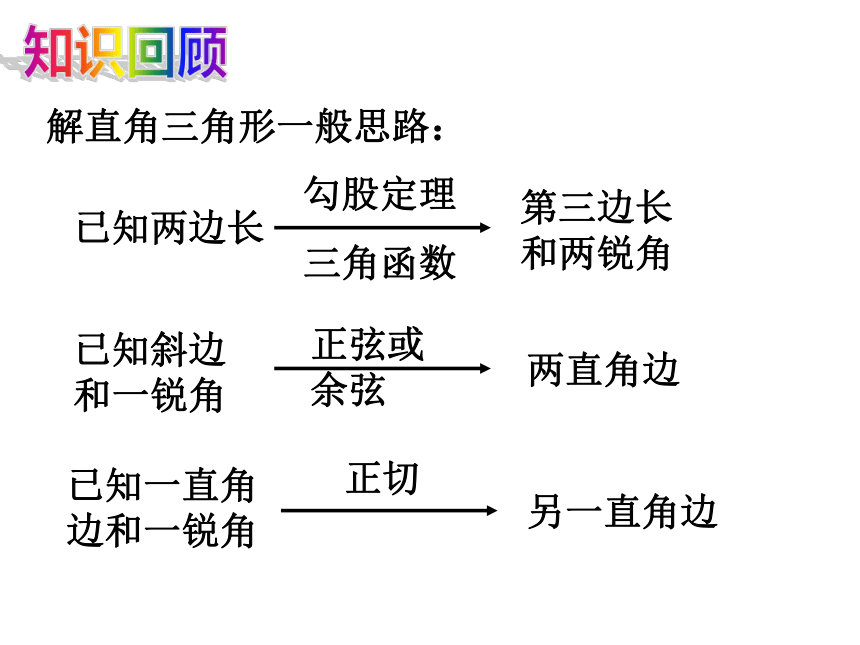
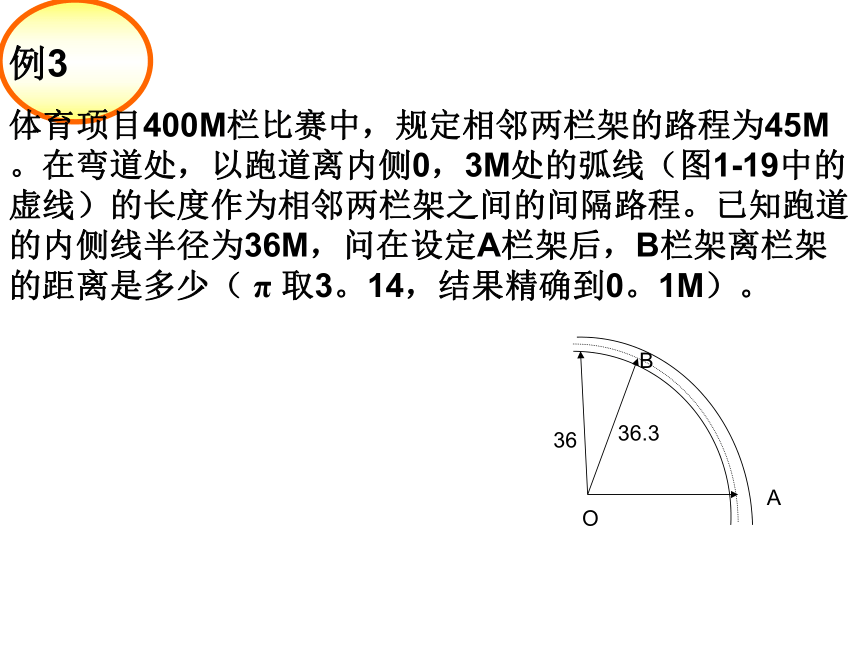
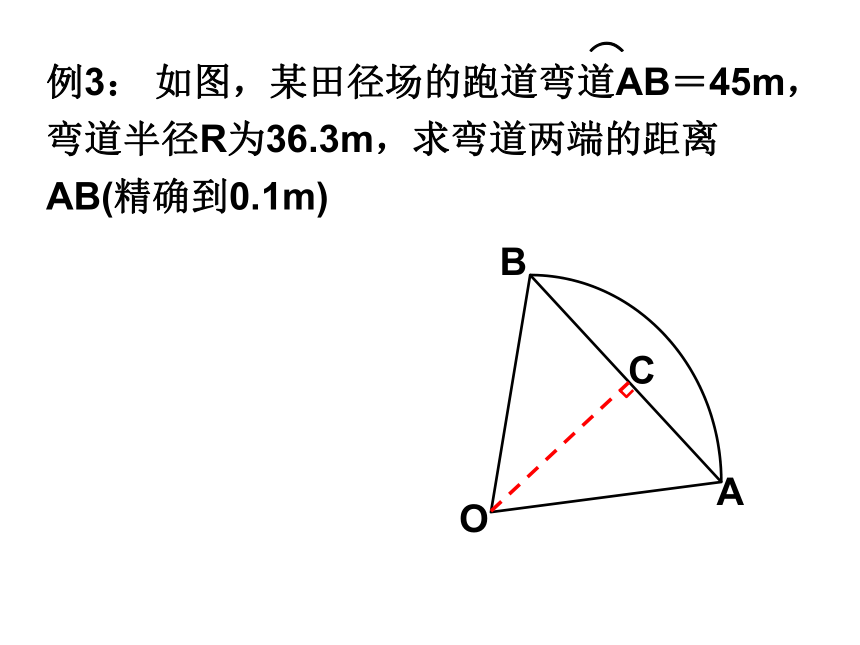
三角函数知识回顾解直角三角形一般思路:已知两边长第三边长和两锐角正弦或余弦已知斜边和一锐角两直角边正切已知一直角边和一锐角另一直角边 生活、生产实践的许多有关图形的计算问题都可以直接通过添加辅助线的方法,转化为解直角三角形的问题来解决.实际应用例3体育项目400M栏比赛中,规定相邻两栏架的路程为45M。在弯道处,以跑道离内侧0,3M处的弧线(图1-19中的虚线)的长度作为相邻两栏架之间的间隔路程。已知跑道的内侧线半径为36M,问在设定A栏架后,B栏架离栏架的距离是多少( π 取3。14,结果精确到0。1M)。3636.3OAB例3: 如图,某田径场的跑道弯道AB=45m,弯道半径R为36.3m,求弯道两端的距离AB(精确到0.1m)OAB⌒修路、挖河、开渠和筑坝时,设计图纸上都要注明斜坡的倾斜程度.
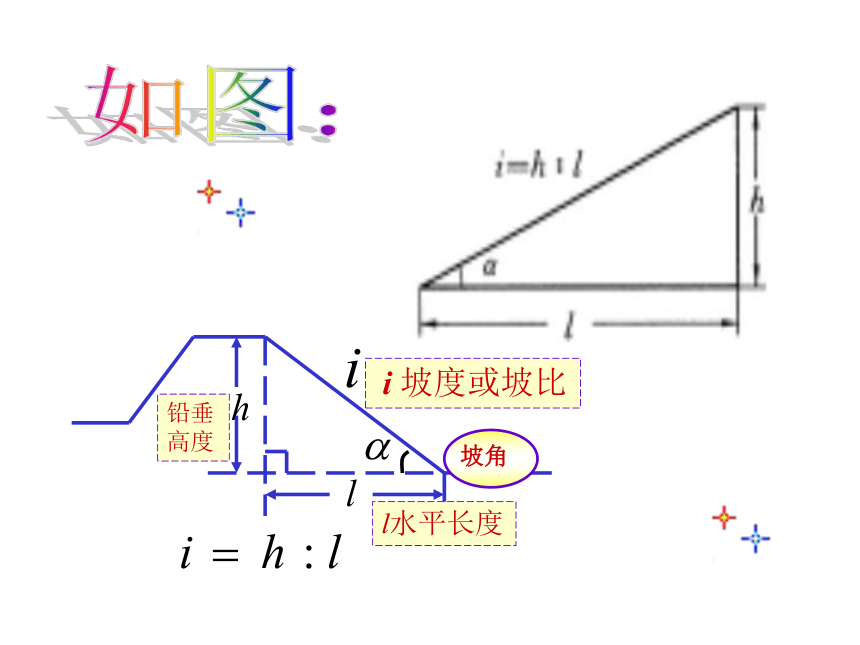
坡面的铅垂高度(h)和水平长度(l)的比叫做坡面坡度(或坡比). 记作i , 即 i = .
坡度通常写成1∶m的形式,如 i=1∶6.坡面与 水平面的夹角叫做坡角,记作α,有
i= = tan α.
显然,坡度越大,坡角α就越大,坡面就越陡. i 坡度或坡比l水平长度铅垂高度如图:一水库大坝的横断面为梯形ABCD,坝顶宽6米,斜坡CD长为60米,斜坡AB的坡度i1=1∶3,斜坡CD的坡度i2=1∶2.5.求:
(1)斜坡CD的坡角与坝底AD的宽度;(长度精确到0.1米)
(2若堤坝长150米。问建造这个堤坝需用多少土石方精确到1立方米?例4 如图一段路基的横断面是梯形,高为4.2米,上底的宽是12.51米,路基的坡面与地面的倾角分别是32°和28°.求路基下底的宽.(精确到0.1米)1. 认清图形中的有关线段;
2. 分析辅助线的作法;
3. 坡角在解题中的作用;
4. 探索解题过程.练习作DE⊥AB,CF⊥AB,垂足分别为E、 F.由题意可知 ?
DE=CF=4.2(米),CD=EF=12.51(米).
在Rt△ADE中,因为
所以 在Rt△BCF中,同理可得
因此 AB=AE+EF+BF
≈6.72+12.51+7.90
≈27.13(米).
答: 路基下底的宽约为27.13米.
例5 如图△ABC中,∠A=45°,AB=6cm,AC=8cm.
(1)求△ABC的面积;
(2)若AB=a,AC=b,AB与AC的夹角为α,你能否用含a、b、 α的式子表示S△ABC?ABC练习1 如图,有一斜坡AB长40m,坡顶离地面的高度为20m,求此斜坡的倾斜角.2.一个锥形零件的轴截面图如图所示。已知倾角α=5.2°,零件的长度l=20cm,大头直径D=10cm,求小头直径d.αDdl4 如图,水库大坝的截面是梯形ABCD,坝顶AD=6m,坡长CD=8m.坡底BC=30m,∠ADC=1350.
(1)求坡角∠ABC的大小;
(2)如果坝长100m,那么修建这个大坝共需多少土石方(结果精确到0.01m3 ).Good Bye!再见
三角函数知识回顾解直角三角形一般思路:已知两边长第三边长和两锐角正弦或余弦已知斜边和一锐角两直角边正切已知一直角边和一锐角另一直角边 生活、生产实践的许多有关图形的计算问题都可以直接通过添加辅助线的方法,转化为解直角三角形的问题来解决.实际应用例3体育项目400M栏比赛中,规定相邻两栏架的路程为45M。在弯道处,以跑道离内侧0,3M处的弧线(图1-19中的虚线)的长度作为相邻两栏架之间的间隔路程。已知跑道的内侧线半径为36M,问在设定A栏架后,B栏架离栏架的距离是多少( π 取3。14,结果精确到0。1M)。3636.3OAB例3: 如图,某田径场的跑道弯道AB=45m,弯道半径R为36.3m,求弯道两端的距离AB(精确到0.1m)OAB⌒修路、挖河、开渠和筑坝时,设计图纸上都要注明斜坡的倾斜程度.
坡面的铅垂高度(h)和水平长度(l)的比叫做坡面坡度(或坡比). 记作i , 即 i = .
坡度通常写成1∶m的形式,如 i=1∶6.坡面与 水平面的夹角叫做坡角,记作α,有
i= = tan α.
显然,坡度越大,坡角α就越大,坡面就越陡. i 坡度或坡比l水平长度铅垂高度如图:一水库大坝的横断面为梯形ABCD,坝顶宽6米,斜坡CD长为60米,斜坡AB的坡度i1=1∶3,斜坡CD的坡度i2=1∶2.5.求:
(1)斜坡CD的坡角与坝底AD的宽度;(长度精确到0.1米)
(2若堤坝长150米。问建造这个堤坝需用多少土石方精确到1立方米?例4 如图一段路基的横断面是梯形,高为4.2米,上底的宽是12.51米,路基的坡面与地面的倾角分别是32°和28°.求路基下底的宽.(精确到0.1米)1. 认清图形中的有关线段;
2. 分析辅助线的作法;
3. 坡角在解题中的作用;
4. 探索解题过程.练习作DE⊥AB,CF⊥AB,垂足分别为E、 F.由题意可知 ?
DE=CF=4.2(米),CD=EF=12.51(米).
在Rt△ADE中,因为
所以 在Rt△BCF中,同理可得
因此 AB=AE+EF+BF
≈6.72+12.51+7.90
≈27.13(米).
答: 路基下底的宽约为27.13米.
例5 如图△ABC中,∠A=45°,AB=6cm,AC=8cm.
(1)求△ABC的面积;
(2)若AB=a,AC=b,AB与AC的夹角为α,你能否用含a、b、 α的式子表示S△ABC?ABC练习1 如图,有一斜坡AB长40m,坡顶离地面的高度为20m,求此斜坡的倾斜角.2.一个锥形零件的轴截面图如图所示。已知倾角α=5.2°,零件的长度l=20cm,大头直径D=10cm,求小头直径d.αDdl4 如图,水库大坝的截面是梯形ABCD,坝顶AD=6m,坡长CD=8m.坡底BC=30m,∠ADC=1350.
(1)求坡角∠ABC的大小;
(2)如果坝长100m,那么修建这个大坝共需多少土石方(结果精确到0.01m3 ).Good Bye!再见
