3.1直线与圆的位置关系(1)[下学期]
文档属性
| 名称 | 3.1直线与圆的位置关系(1)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 789.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-05-25 00:00:00 | ||
图片预览




文档简介
课件22张PPT。直线与圆的位置关系执教:唐文斌操作:
在纸上画一个圆O(看作是太阳), 把直尺的边缘看作一条直线l(海平面),在纸上移动直尺。模拟日出问:
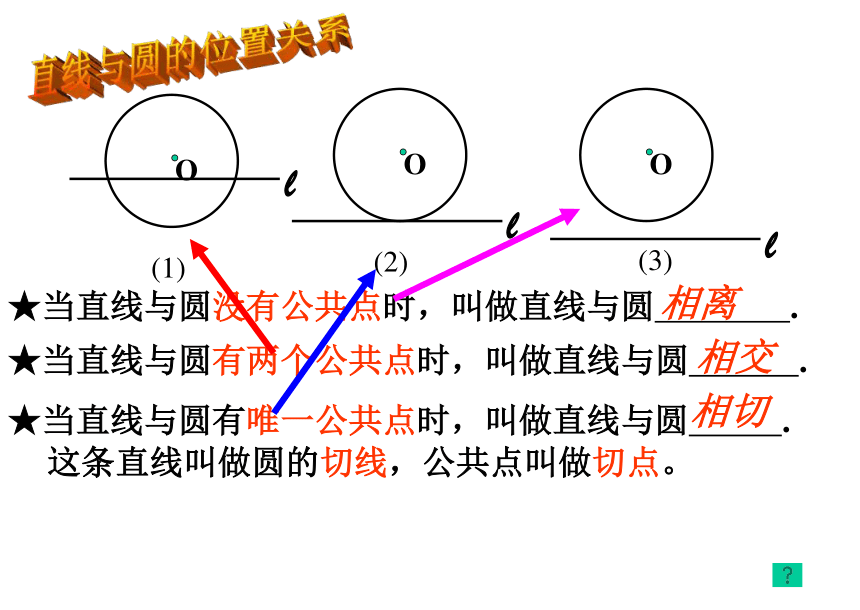
你发现直线l与圆O的
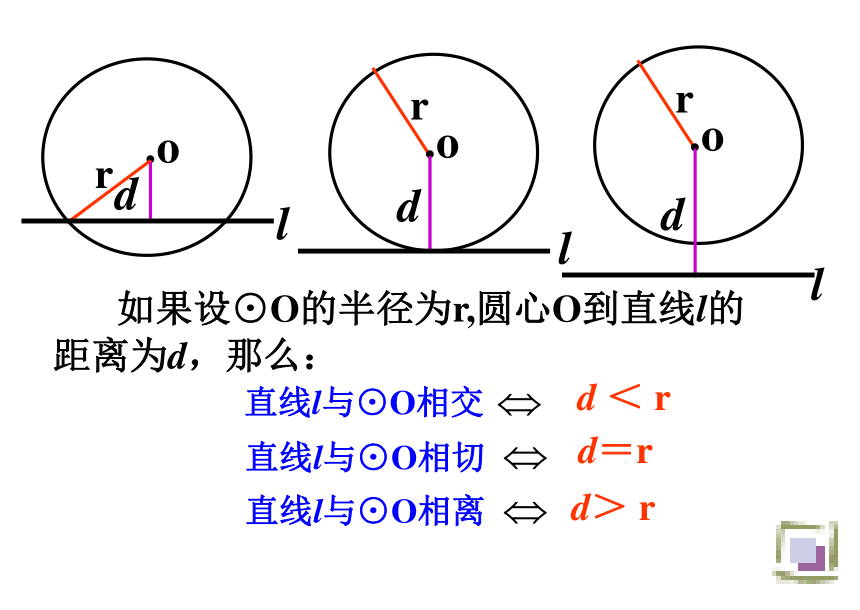
位置关系有几种?★当直线与圆有唯一公共点时,叫做直线与圆 .★当直线与圆没有公共点时,叫做直线与圆 . ★当直线与圆有两个公共点时,叫做直线与圆 . 相离相切相交直线与圆的位置关系(1)(3)(2)这条直线叫做圆的切线,公共点叫做切点。OOOlll.orddd 如果设⊙O的半径为r,圆心O到直线l的距离为d,那么:lll直线l与⊙O相交d < r直线l与⊙O相切d=r直线l与⊙O相离d> r 设⊙O的半径为r,圆心O到直线l的距离为d。根据下列条件判断直线l与⊙O的位置关系。抢答,我能行(2)d=1,r= ; (3)d=2,r=2; (1)d=4,r=3;∵ d < r
∴直线l与⊙O相交∵d=r
∴直线l与⊙O相切∵d> r
∴直线l与⊙O相离梳理:判定直线与圆的位置关系的方法有____种:(1)由________________ 的个数来判断;(2)由_______________________________的数量大小关系来判断.注意:在实际应用中,常采用第二种方法判定.两直线 与圆的公共点圆心到直线的距离d与半径r
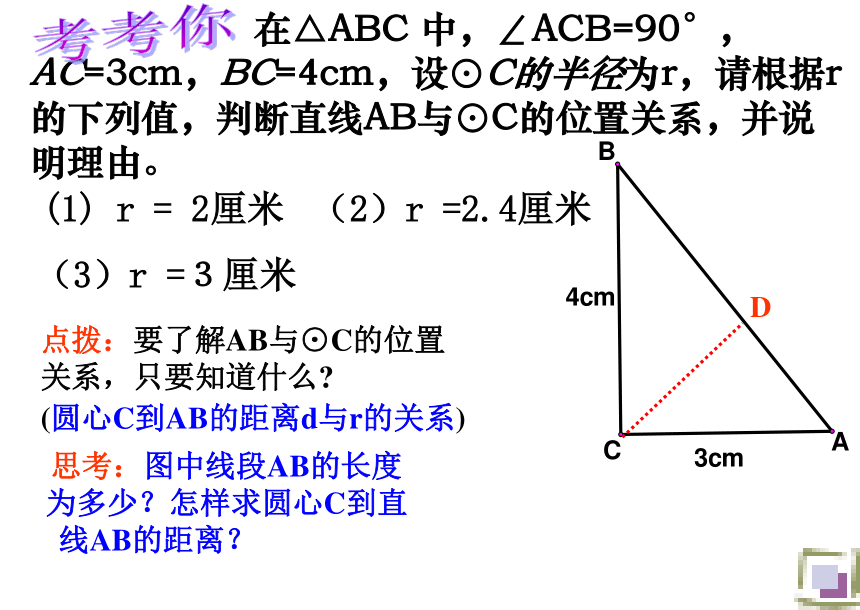
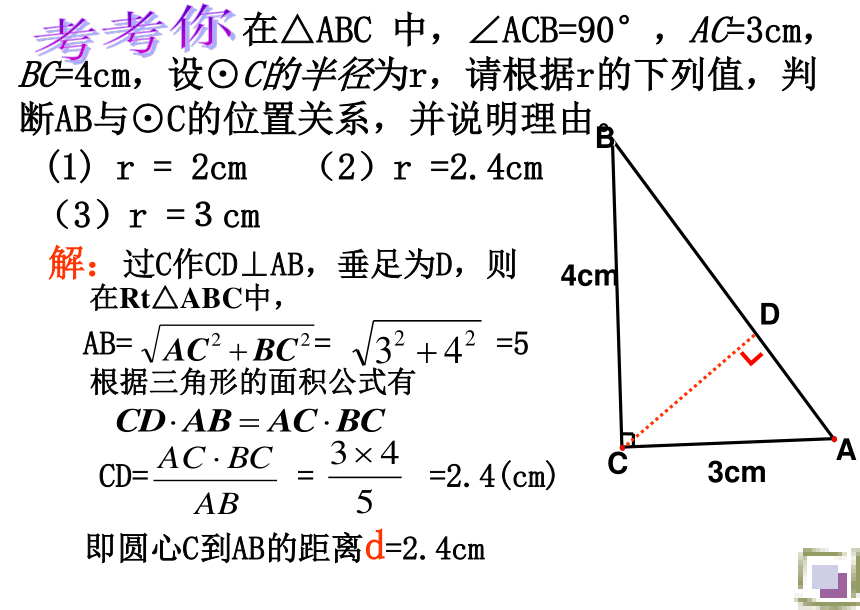
在△ABC 中,∠ACB=90°,AC=3cm,BC=4cm,设⊙C的半径为r,请根据r的下列值,判断直线AB与⊙C的位置关系,并说明理由。(1) r = 2厘米(2)r =2.4厘米(3)r =3厘米考考你D点拨:要了解AB与⊙C的位置
关系,只要知道什么?思考:图中线段AB的长度
为多少?怎样求圆心C到直
线AB的距离? (圆心C到AB的距离d与r的关系)CD= = =2.4(cm)
AB= = =5即圆心C到AB的距离d=2.4cm解:过C作CD⊥AB,垂足为D,则 在△ABC 中,∠ACB=90°,AC=3cm,BC=4cm,设⊙C的半径为r,请根据r的下列值,判断AB与⊙C的位置关系,并说明理由。(1) r = 2cm(2)r =2.4cm(3)r =3cm 考考你在Rt△ABC中,根据三角形的面积公式有4cm3cmDACB┏ABCD3cm4cm(1) r = 2(2)r =2.4ABCD3cm4cm(3)r =3ABCD3cm4cm当r =2cm时,
d > r,
∴☉C 与
直线AB相离; 当r =2.4cm时,
d = r,
∴☉C 与直线AB相切; 当r =3cm时,
d < r,
∴☉C 与直线AB相交。2.4cm2.4cm2.4cm讨论:在Rt△ABC中,∠C=90°,AC=3cm,
BC=4cm,以C为圆心,r为半径作圆。1、当r满足________________时,⊙C与直线AB相离。2、当r满足____________ 时,⊙C与直线AB相切。3、当r满足____________时,
⊙C与直线AB相交。BCAD45d=2.4cm30cmAC=3cm,BC=4cm,设⊙C的半径为r。知识拓展ABCD3cm2.4cm当r满足_______________ 时,⊙C与线段AB只有一个公共点.4cm在Rt△ABC中,∠C=90°,AC=3cm,
BC=4cm,以C为圆心,r为半径作圆。当r满足 时,
⊙C与线段AB只有一个公共点。BCAD45d=2.4cm3r =2.4cm 或3cm <r ≤4cm知识拓展 如图,在码头A的北偏东60°方向有一个海岛,离该岛中心P的8海里范围内是一个暗礁区。货船从码头A由西向东方向航行,行驶了18海里到达B,这时岛中心P在北偏东30°方向。若货船不改变航向,问货船会不会进入暗礁区?学以致用 在码头A的北偏东60°方向有一个海岛,离该岛中心P的15海里范围内是一个暗礁区。货船从码头A由西向东方向航行,行驶了18海里到达B,这时岛中心P在北偏东30°方向。若货船不改变航向,问货船会不会进入暗礁区?解:如图,作PH⊥AB,垂足为H.则∠PAH=30°,∠PBH=60°,∴∠APB=∠PBH-∠PAB=30°∴AB=BP=18(海里)∴PH=BPsin∠PBH∴货船不会进入暗礁区=18sin60°学以致用点拨:圆心A到X轴、
Y轴的距离各是多少?.AO1、已知⊙A的直径为6,点A的坐标为(-3,-4),则⊙A与X轴的位置关系是_____,⊙A与Y轴的位置关系是______。BC43相离相切练一练2、已知正方形ABCD的边长为2,以对角线的交点O为圆心,以1为半径画圆,则⊙O与正方形四边的位置关系为 。相切E 3、已知⊙O的半径为3,点A在直线l上,点A到⊙O的圆心O的距离为3,则l与⊙O的位置关系为 。相切或相交··OOAA ll说说收获直线与圆的位置关系2 个交点割线1 个切点切线d < rd = rd > r没有 已知⊙O的半径为r,点O到直线l的距离为d,且|d-3|+(6-2r)2=0.试判断直线与⊙O的位置关系。思维体操布置作业:1、必做题:教材P502、3
2、选做题:教材 P505
谢谢光临指导
你发现直线l与圆O的
位置关系有几种?★当直线与圆有唯一公共点时,叫做直线与圆 .★当直线与圆没有公共点时,叫做直线与圆 . ★当直线与圆有两个公共点时,叫做直线与圆 . 相离相切相交直线与圆的位置关系(1)(3)(2)这条直线叫做圆的切线,公共点叫做切点。OOOlll.orddd 如果设⊙O的半径为r,圆心O到直线l的距离为d,那么:lll直线l与⊙O相交d < r直线l与⊙O相切d=r直线l与⊙O相离d> r 设⊙O的半径为r,圆心O到直线l的距离为d。根据下列条件判断直线l与⊙O的位置关系。抢答,我能行(2)d=1,r= ; (3)d=2,r=2; (1)d=4,r=3;∵ d < r
∴直线l与⊙O相交∵d=r
∴直线l与⊙O相切∵d> r
∴直线l与⊙O相离梳理:判定直线与圆的位置关系的方法有____种:(1)由________________ 的个数来判断;(2)由_______________________________的数量大小关系来判断.注意:在实际应用中,常采用第二种方法判定.两直线 与圆的公共点圆心到直线的距离d与半径r
在△ABC 中,∠ACB=90°,AC=3cm,BC=4cm,设⊙C的半径为r,请根据r的下列值,判断直线AB与⊙C的位置关系,并说明理由。(1) r = 2厘米(2)r =2.4厘米(3)r =3厘米考考你D点拨:要了解AB与⊙C的位置
关系,只要知道什么?思考:图中线段AB的长度
为多少?怎样求圆心C到直
线AB的距离? (圆心C到AB的距离d与r的关系)CD= = =2.4(cm)
AB= = =5即圆心C到AB的距离d=2.4cm解:过C作CD⊥AB,垂足为D,则 在△ABC 中,∠ACB=90°,AC=3cm,BC=4cm,设⊙C的半径为r,请根据r的下列值,判断AB与⊙C的位置关系,并说明理由。(1) r = 2cm(2)r =2.4cm(3)r =3cm 考考你在Rt△ABC中,根据三角形的面积公式有4cm3cmDACB┏ABCD3cm4cm(1) r = 2(2)r =2.4ABCD3cm4cm(3)r =3ABCD3cm4cm当r =2cm时,
d > r,
∴☉C 与
直线AB相离; 当r =2.4cm时,
d = r,
∴☉C 与直线AB相切; 当r =3cm时,
d < r,
∴☉C 与直线AB相交。2.4cm2.4cm2.4cm讨论:在Rt△ABC中,∠C=90°,AC=3cm,
BC=4cm,以C为圆心,r为半径作圆。1、当r满足________________时,⊙C与直线AB相离。2、当r满足____________ 时,⊙C与直线AB相切。3、当r满足____________时,
⊙C与直线AB相交。BCAD45d=2.4cm30cm
BC=4cm,以C为圆心,r为半径作圆。当r满足 时,
⊙C与线段AB只有一个公共点。BCAD45d=2.4cm3r =2.4cm 或3cm <r ≤4cm知识拓展 如图,在码头A的北偏东60°方向有一个海岛,离该岛中心P的8海里范围内是一个暗礁区。货船从码头A由西向东方向航行,行驶了18海里到达B,这时岛中心P在北偏东30°方向。若货船不改变航向,问货船会不会进入暗礁区?学以致用 在码头A的北偏东60°方向有一个海岛,离该岛中心P的15海里范围内是一个暗礁区。货船从码头A由西向东方向航行,行驶了18海里到达B,这时岛中心P在北偏东30°方向。若货船不改变航向,问货船会不会进入暗礁区?解:如图,作PH⊥AB,垂足为H.则∠PAH=30°,∠PBH=60°,∴∠APB=∠PBH-∠PAB=30°∴AB=BP=18(海里)∴PH=BPsin∠PBH∴货船不会进入暗礁区=18sin60°学以致用点拨:圆心A到X轴、
Y轴的距离各是多少?.AO1、已知⊙A的直径为6,点A的坐标为(-3,-4),则⊙A与X轴的位置关系是_____,⊙A与Y轴的位置关系是______。BC43相离相切练一练2、已知正方形ABCD的边长为2,以对角线的交点O为圆心,以1为半径画圆,则⊙O与正方形四边的位置关系为 。相切E 3、已知⊙O的半径为3,点A在直线l上,点A到⊙O的圆心O的距离为3,则l与⊙O的位置关系为 。相切或相交··OOAA ll说说收获直线与圆的位置关系2 个交点割线1 个切点切线d < rd = rd > r没有 已知⊙O的半径为r,点O到直线l的距离为d,且|d-3|+(6-2r)2=0.试判断直线与⊙O的位置关系。思维体操布置作业:1、必做题:教材P502、3
2、选做题:教材 P505
谢谢光临指导
