3.1直线与圆的位置关系(2)[下学期]
文档属性
| 名称 | 3.1直线与圆的位置关系(2)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 468.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-05-25 00:00:00 | ||
图片预览



文档简介
课件13张PPT。3.1直线与圆的位置关系(2)浙教版数学九年级(下)旧知回顾直线与圆的位置关系有下面的性质:如果⊙O的半径为r,圆心O到直线l 的距离为d,那么新课引入请按照下述步骤作图:
如图,在⊙O上任取一点A,连结OA,,过点A作直线l⊥OA,OA思考以下问题:
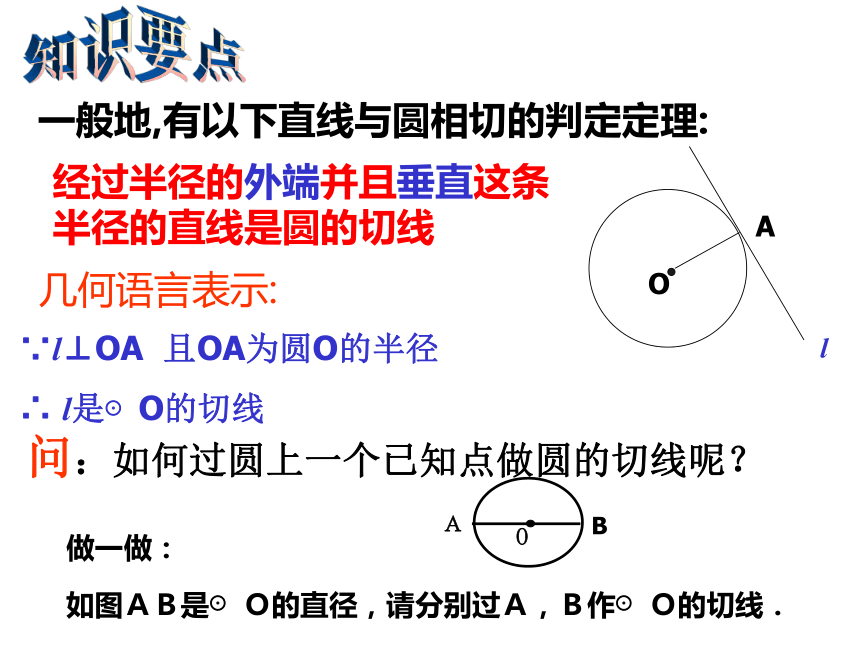
(1)圆心O到直线l 的距离和圆的半径有什么关系?(2)直线l 和⊙ O的位置有什么关系?根据什么?(3)由此你发现了什么?相等d=r相切知识要点一般地,有以下直线与圆相切的判定定理:经过半径的外端并且垂直这条半径的直线是圆的切线∵l⊥OA 且OA为圆O的半径
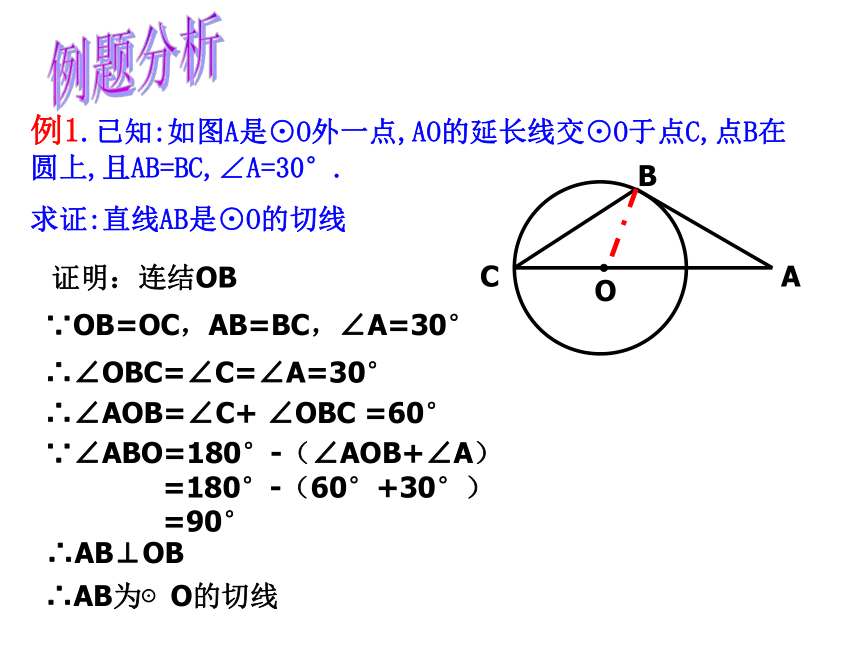
∴ l是⊙O的切线几何语言表示:问:如何过圆上一个已知点做圆的切线呢?例题分析例1.已知:如图A是⊙O外一点,AO的延长线交⊙O于点C,点B在圆上,且AB=BC,∠A=30°.
求证:直线AB是⊙O的切线证明:连结OB∵OB=OC,AB=BC,∠A=30°∴∠OBC=∠C=∠A=30°∴∠AOB=∠C+ ∠OBC =60°∵∠ABO=180°-(∠AOB+∠A)
=180°-(60°+30°)
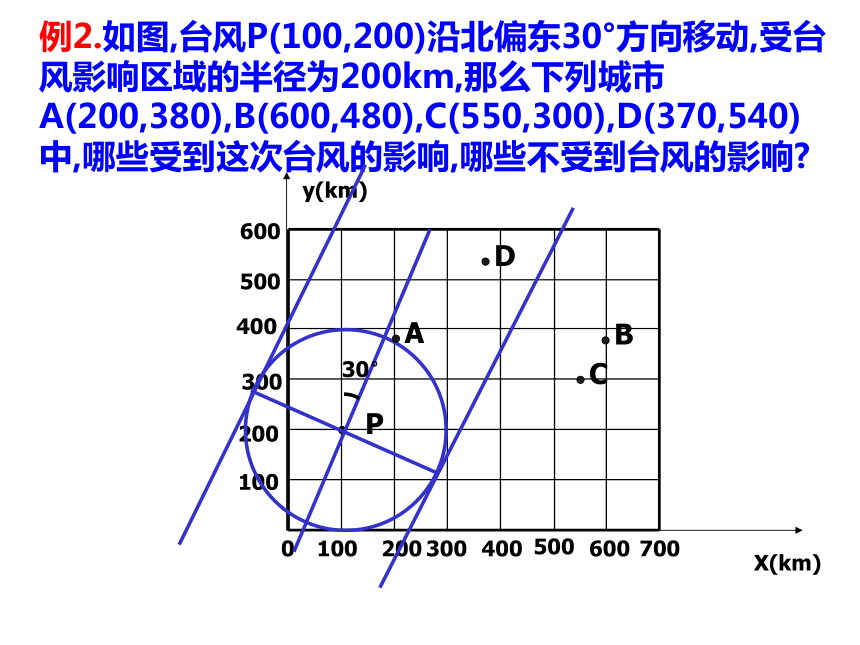
=90°∴AB⊥OB∴AB为⊙O的切线例2.如图,台风P(100,200)沿北偏东30°方向移动,受台风影响区域的半径为200km,那么下列城市A(200,380),B(600,480),C(550,300),D(370,540)中,哪些受到这次台风的影响,哪些不受到台风的影响?0100400500600700300200X(km)y(km)60050040030020010030°P课内练习1.如图,Q在⊙O上,分别根据下列条件,判定直线PQ与⊙O是否相切:
(1)OQ=6,OP=10,PQ=8
(2)∠O=67.3°,∠P=22°42′2.如图,OP是⊙O的半径,∠POT=60°,
OT交⊙O于S点.
(1)过点P作⊙O的切线.
(2)过点P的切线交OT于Q,判断S是不是OQ的中点,并说明理由.探究活动请任意画一个圆,并在这个圆所在的平面内任意取一点P.
(1)过点P是否都能作这个圆的切线?
(2)点P在什么位置时,能作并且只能作一条切线?
(3)点P在什么位置时,能作两条切线?这两条切线有什么特性?
(4)能作多于2条的切线吗?点在圆内不能作切线点在圆上点在圆外相等不能小结经过半径的外端并且垂直这条半径的直线是圆的切线切线的判定定理:这个定理不仅可以用来判定圆的切线,还可以依据它来画切线.在判定切线的时候,如果已知点在圆上,则连半径是常用的辅助线综合运用1、如图,已知AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC.
(1)求证:DE是⊙O的切线.
(2)若∠C=30°,CD=10cm,求⊙O的半径.OABCDE2、如图,在Rt△ABC中,∠ACB=Rt∠,CD⊥AB于点D。
(1)求证:BC是△ADC的外接圆的切线;
(2) △BDC的外接圆的切线是哪一条?为什么?
(3)若AC=5,BC=12,以C为圆心作圆C,使圆C与 AB相切,则圆C的半径是多少?综合运用3、如图,AB是⊙O的直径,BC切⊙O于点B,连结OC,过A作AD∥OC,交⊙O于点D,连结DC。求证:CD是⊙O的切线。
如图,在⊙O上任取一点A,连结OA,,过点A作直线l⊥OA,OA思考以下问题:
(1)圆心O到直线l 的距离和圆的半径有什么关系?(2)直线l 和⊙ O的位置有什么关系?根据什么?(3)由此你发现了什么?相等d=r相切知识要点一般地,有以下直线与圆相切的判定定理:经过半径的外端并且垂直这条半径的直线是圆的切线∵l⊥OA 且OA为圆O的半径
∴ l是⊙O的切线几何语言表示:问:如何过圆上一个已知点做圆的切线呢?例题分析例1.已知:如图A是⊙O外一点,AO的延长线交⊙O于点C,点B在圆上,且AB=BC,∠A=30°.
求证:直线AB是⊙O的切线证明:连结OB∵OB=OC,AB=BC,∠A=30°∴∠OBC=∠C=∠A=30°∴∠AOB=∠C+ ∠OBC =60°∵∠ABO=180°-(∠AOB+∠A)
=180°-(60°+30°)
=90°∴AB⊥OB∴AB为⊙O的切线例2.如图,台风P(100,200)沿北偏东30°方向移动,受台风影响区域的半径为200km,那么下列城市A(200,380),B(600,480),C(550,300),D(370,540)中,哪些受到这次台风的影响,哪些不受到台风的影响?0100400500600700300200X(km)y(km)60050040030020010030°P课内练习1.如图,Q在⊙O上,分别根据下列条件,判定直线PQ与⊙O是否相切:
(1)OQ=6,OP=10,PQ=8
(2)∠O=67.3°,∠P=22°42′2.如图,OP是⊙O的半径,∠POT=60°,
OT交⊙O于S点.
(1)过点P作⊙O的切线.
(2)过点P的切线交OT于Q,判断S是不是OQ的中点,并说明理由.探究活动请任意画一个圆,并在这个圆所在的平面内任意取一点P.
(1)过点P是否都能作这个圆的切线?
(2)点P在什么位置时,能作并且只能作一条切线?
(3)点P在什么位置时,能作两条切线?这两条切线有什么特性?
(4)能作多于2条的切线吗?点在圆内不能作切线点在圆上点在圆外相等不能小结经过半径的外端并且垂直这条半径的直线是圆的切线切线的判定定理:这个定理不仅可以用来判定圆的切线,还可以依据它来画切线.在判定切线的时候,如果已知点在圆上,则连半径是常用的辅助线综合运用1、如图,已知AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC.
(1)求证:DE是⊙O的切线.
(2)若∠C=30°,CD=10cm,求⊙O的半径.OABCDE2、如图,在Rt△ABC中,∠ACB=Rt∠,CD⊥AB于点D。
(1)求证:BC是△ADC的外接圆的切线;
(2) △BDC的外接圆的切线是哪一条?为什么?
(3)若AC=5,BC=12,以C为圆心作圆C,使圆C与 AB相切,则圆C的半径是多少?综合运用3、如图,AB是⊙O的直径,BC切⊙O于点B,连结OC,过A作AD∥OC,交⊙O于点D,连结DC。求证:CD是⊙O的切线。
