3.1直线与圆的位置关系(2)[下学期]
文档属性
| 名称 | 3.1直线与圆的位置关系(2)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 624.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-05-25 20:31:00 | ||
图片预览




文档简介
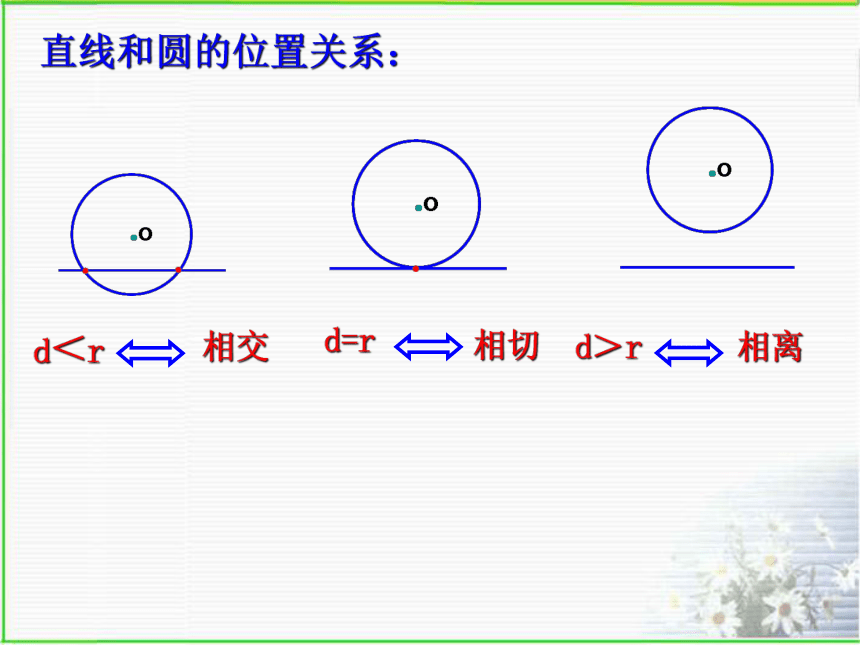
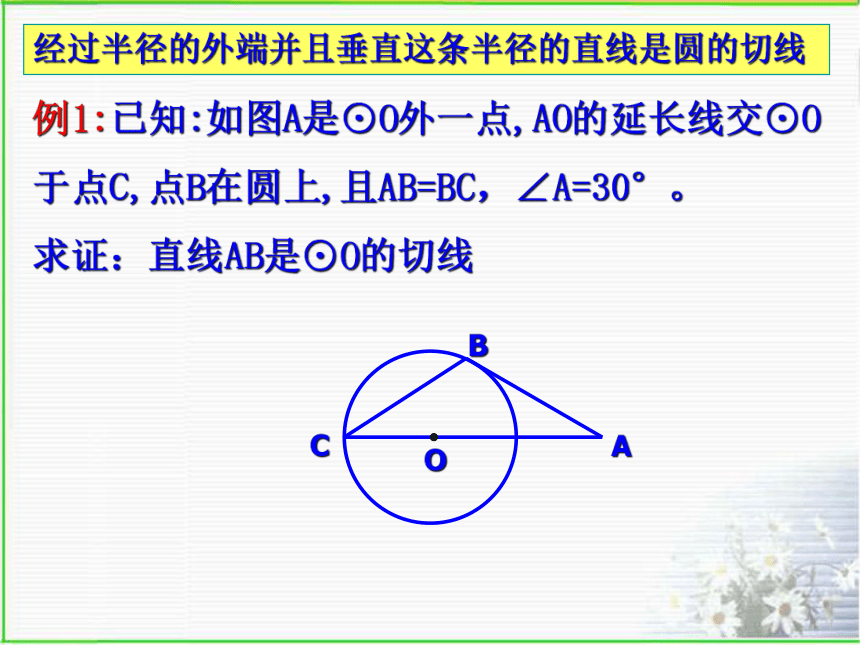
课件12张PPT。3.1直线与圆的位置关系(2)直线和圆的位置关系:l 相交 相切相离请按照下述步骤作图: 如图,在⊙O上任取一点A,连结OA,过点A作直线l⊥OA。(1)圆心O到直线l的距离和圆的半径有什么关系?(2)直线l和⊙O的位置有什么关系?根据什么?(3)由此你发现怎样的直线是切线?经过半径的外端并且垂直这条半径的直线是圆的切线。切线的判定定理:经过半径的外端并且垂直这条半径的直线是圆的切线。半径的外端垂直这条半径例1:已知:如图A是⊙O外一点,AO的延长线交⊙O于点C,点B在圆上,且AB=BC,∠A=30°。
求证:直线AB是⊙O的切线经过半径的外端并且垂直这条半径的直线是圆的切线做一做:如图,已知点B在⊙O上。根据下列条件,能否判定直线AB和⊙O相切?⑴ OB=6,AO=10,AB=8⑵ ∠O=68.5°,∠A=21°30′经过半径的外端并且垂直这条半径的直线是圆的切线做一做:如图AB是⊙O的直径,请分别过A,B作⊙O的切线.例2:如图,台风P(100,200)沿北偏东30°方向移动,受台风影响区域的半径为200km,那么下列城市(200,380),
B(600,480),C(550,300),D(370,540)中,哪些受到这次台风的影响,哪些不受到台风的影响?0100400500600700300200X(km)y(km)60050040030020010030°POPST做一做:如图,OP是⊙O的半径,∠POT=60°,OT交⊙O于S点。
(1)过点P作⊙O的切线.
(2)过点P的切线交OT于Q,判断S是不是OQ的中点,并说明理由.1、切线的判定定理:经过半径外端并且垂直于这条半径的直线是圆的切线。本节小结3、学会过圆上一点画切线.2、证明切线时常用的辅助线:作半径探究活动:请任意画一个圆,并在这个圆所在的平面内任意取一点P.
(1)过点P是否都能作这个圆的切线?
(2)点P在什么位置时,能作并且只能作一条切线?
(3)点P在什么位置时,能作两条切线?这两条切线有什么特性?
(4)能作多于2条的切线吗?体会.分享说能出你这节课的收获和体验让大家与你分享吗?
