1.1锐角三角函数(1)
图片预览



文档简介
课件27张PPT。九年级下
第一章
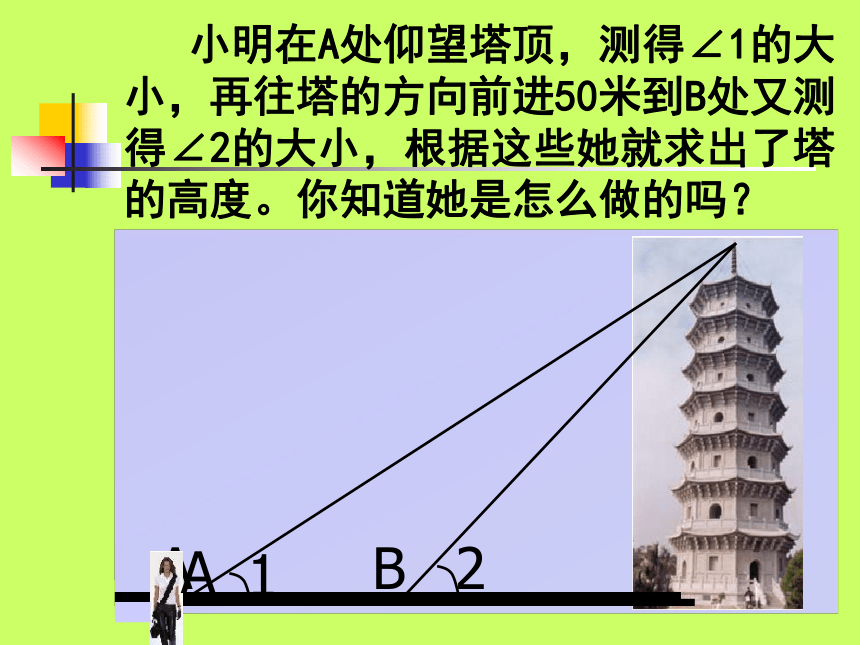
直角三角形的边角关系 小明在A处仰望塔顶,测得∠1的大小,再往塔的方向前进50米到B处又测得∠2的大小,根据这些她就求出了塔的高度。你知道她是怎么做的吗?
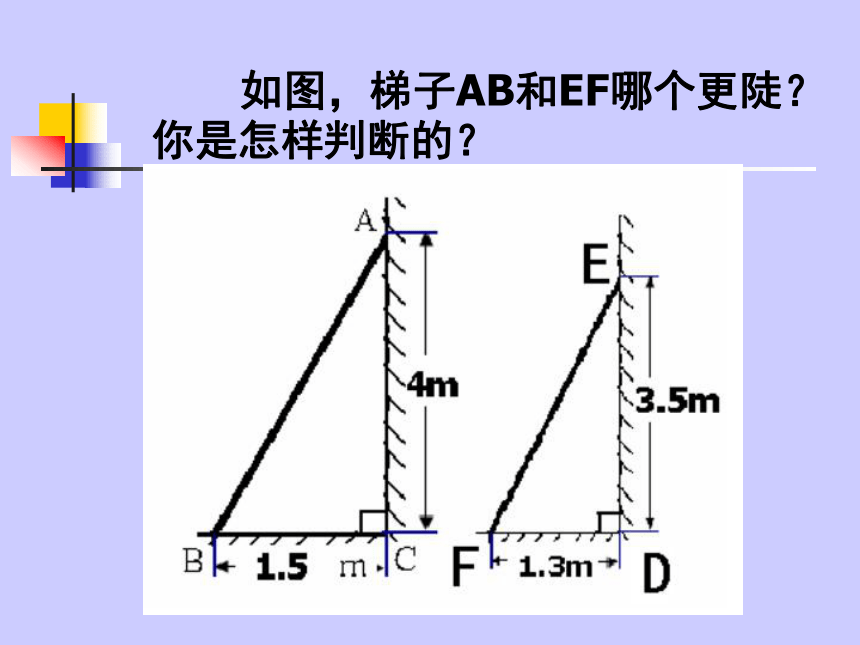
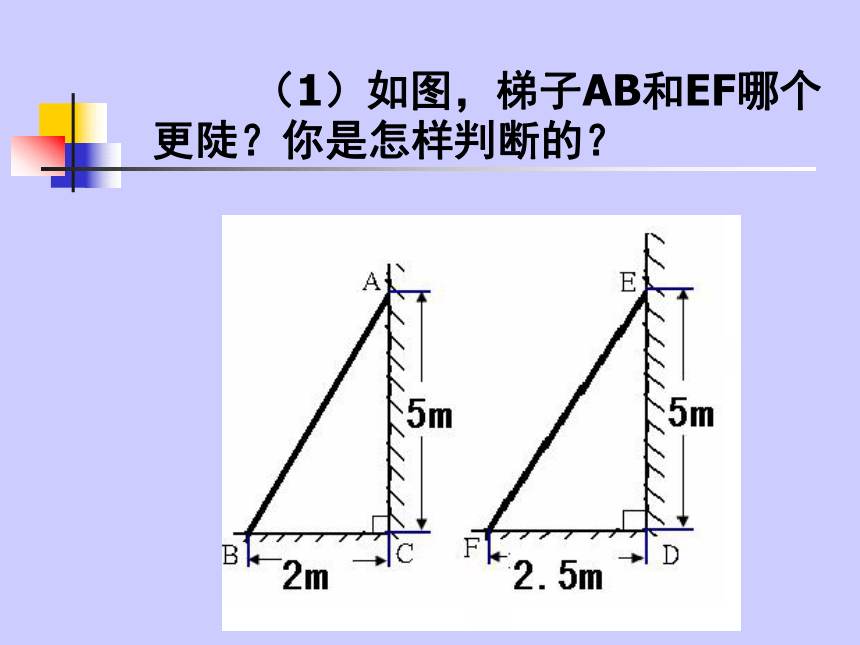
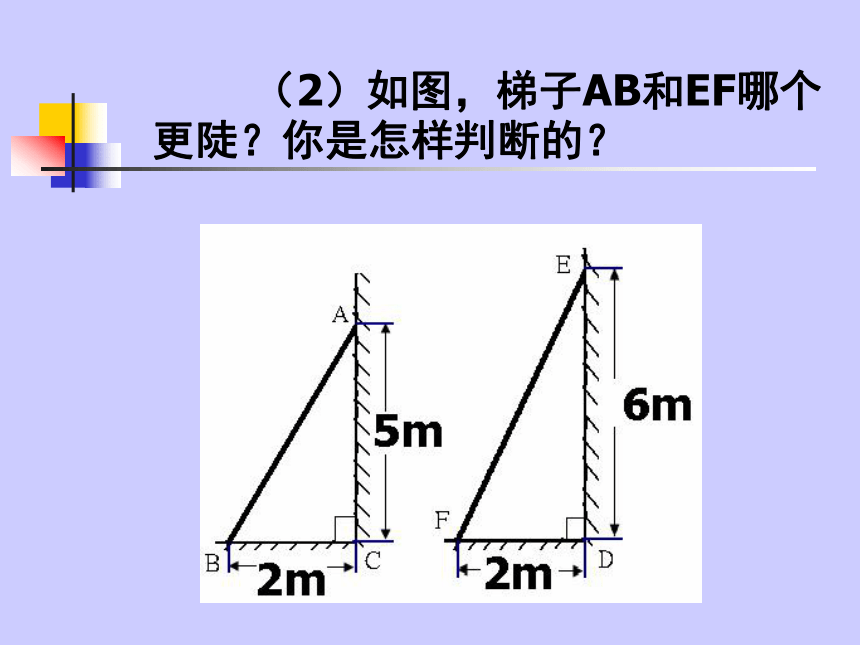
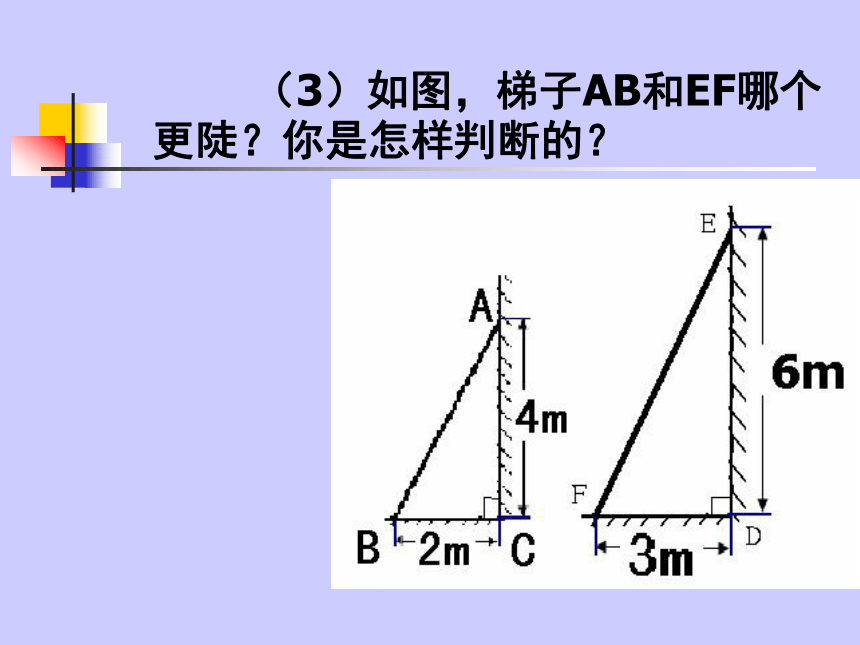
A梯子是我们日常生活中常见的物体 你能比较两个梯子哪个更陡吗?你有哪些办法? 如图,梯子AB和EF哪个更陡?你是怎样判断的? (1)如图,梯子AB和EF哪个更陡?你是怎样判断的? (2)如图,梯子AB和EF哪个更陡?你是怎样判断的? 在直角三角形中,若一个锐角的对边与邻边的比值是一个定值,那么这个角的值也随之确定。 想一想:
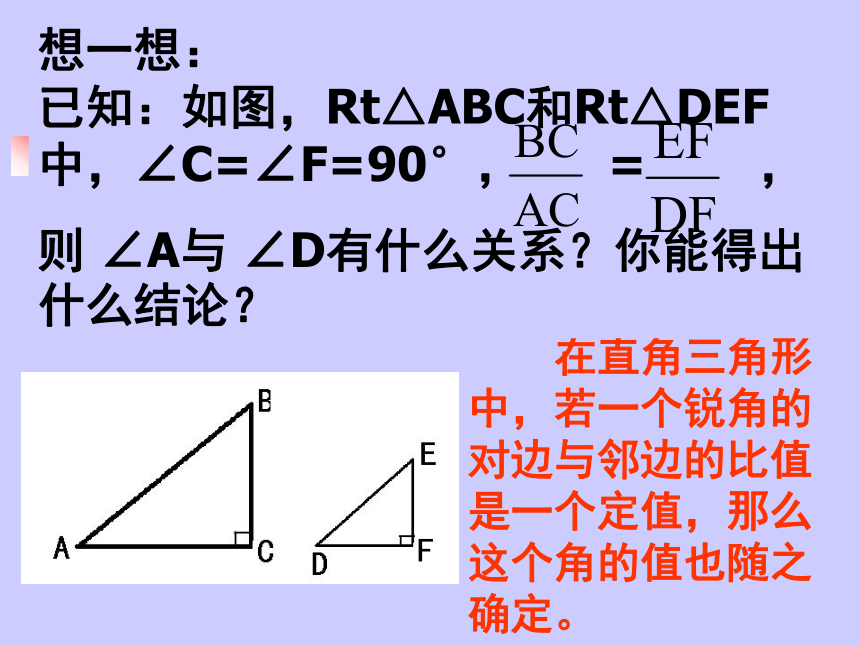
已知:如图,Rt△ABC和Rt△DEF中,∠C=∠F=90°, ∠A=∠D,
则 与 有什么关系? 由此你又能得出什么结论? 一、正切的定义:
在Rt△ABC中,锐角A的对边与邻边的比叫做∠A的正切,记作tanA,即
tanA= 思考:1、判断对错:
如图, 1) tanA=
2、在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值( )A、扩大100倍 B、缩小100倍 C、不变 D、不能确定3、已知∠A、∠B为锐角
(1) 若∠A=∠B,则tanA tanB
(2)若tanA=tanB,则∠A ∠B。 定义中应该注意的几个问题: 1、tanA是在直角三角形中定义的,∠A是一个锐角(注意数形结合,构造直角三角形) 2、tanA是一个完整的符号,表示∠A的正切,习惯省去“∠”; 3、tanA是一个比值(直角边之比,注意比的顺序: );且tanA﹥0,无单位; 4、tanA的大小只与∠A的大小有关,而与直角三角形的边长无关。 5、角相等,则正切值相等;两锐角的正切值相等,则这两个锐角相等。 1、在右图中 求tanA的值
随堂练习(一): 2.如图,△ABC是等腰直角三角形,你能根据图中所给数据求出tanC吗? 3.∠C=90°CD⊥AB,
tanB=
4、在上图中,若BD=6,CD=12,求tanA的值。 例1:在Rt△ABC中,∠C=90°, (1)AC=3,AB=6,求tanA和tanB
(2)BC=3,tanA= ,求AC 和AB。
2、在等腰△ABC中,AB=AC=13,BC=10,求tanB。练习(二) 1、在Rt△ABC中,∠C=90°,
AB=15,tanA= ,求AC和BC。议一议:
梯子的倾斜程度与tanA有什么关系? tanA的值越大,梯子越陡,∠A越大; ∠A越大,梯子越陡,tanA的值越大。 试一试: 如图,梯子AB和EF哪个更陡? 1、正切的定义。
2、梯子的倾斜程度与tanA的关系。 (∠A和tanA之间的关系)。
3、数形结合的方法;构造直角三角形的意识;方程思想。
4、“一般 特殊 一般”的数学思想方法。回顾、反思、深化:相信自己:(必做题)
1、在Rt△ABC中,∠C=90°, (1)AC=25,AB=27,求tanA和tanB
(2)BC=3,tanA=0.6,求AC 和AB。
(3)AC=4,tanA=0.8,求BC。
2、在梯形ABCD中,AD//BC,AB=DC=13,AD=8, BC=18,求tanB。挑战自己:(选做题) 1、在△ABC中,D是AB的中点,DC⊥AC,tan∠BCD=0.5,AB=4 ,求AC。谢谢听课试一试: 如图表示两个自动扶梯,哪一个自动扶梯比较陡? 甲 乙
第一章
直角三角形的边角关系 小明在A处仰望塔顶,测得∠1的大小,再往塔的方向前进50米到B处又测得∠2的大小,根据这些她就求出了塔的高度。你知道她是怎么做的吗?
A梯子是我们日常生活中常见的物体 你能比较两个梯子哪个更陡吗?你有哪些办法? 如图,梯子AB和EF哪个更陡?你是怎样判断的? (1)如图,梯子AB和EF哪个更陡?你是怎样判断的? (2)如图,梯子AB和EF哪个更陡?你是怎样判断的? 在直角三角形中,若一个锐角的对边与邻边的比值是一个定值,那么这个角的值也随之确定。 想一想:
已知:如图,Rt△ABC和Rt△DEF中,∠C=∠F=90°, ∠A=∠D,
则 与 有什么关系? 由此你又能得出什么结论? 一、正切的定义:
在Rt△ABC中,锐角A的对边与邻边的比叫做∠A的正切,记作tanA,即
tanA= 思考:1、判断对错:
如图, 1) tanA=
2、在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值( )A、扩大100倍 B、缩小100倍 C、不变 D、不能确定3、已知∠A、∠B为锐角
(1) 若∠A=∠B,则tanA tanB
(2)若tanA=tanB,则∠A ∠B。 定义中应该注意的几个问题: 1、tanA是在直角三角形中定义的,∠A是一个锐角(注意数形结合,构造直角三角形) 2、tanA是一个完整的符号,表示∠A的正切,习惯省去“∠”; 3、tanA是一个比值(直角边之比,注意比的顺序: );且tanA﹥0,无单位; 4、tanA的大小只与∠A的大小有关,而与直角三角形的边长无关。 5、角相等,则正切值相等;两锐角的正切值相等,则这两个锐角相等。 1、在右图中 求tanA的值
随堂练习(一): 2.如图,△ABC是等腰直角三角形,你能根据图中所给数据求出tanC吗? 3.∠C=90°CD⊥AB,
tanB=
4、在上图中,若BD=6,CD=12,求tanA的值。 例1:在Rt△ABC中,∠C=90°, (1)AC=3,AB=6,求tanA和tanB
(2)BC=3,tanA= ,求AC 和AB。
2、在等腰△ABC中,AB=AC=13,BC=10,求tanB。练习(二) 1、在Rt△ABC中,∠C=90°,
AB=15,tanA= ,求AC和BC。议一议:
梯子的倾斜程度与tanA有什么关系? tanA的值越大,梯子越陡,∠A越大; ∠A越大,梯子越陡,tanA的值越大。 试一试: 如图,梯子AB和EF哪个更陡? 1、正切的定义。
2、梯子的倾斜程度与tanA的关系。 (∠A和tanA之间的关系)。
3、数形结合的方法;构造直角三角形的意识;方程思想。
4、“一般 特殊 一般”的数学思想方法。回顾、反思、深化:相信自己:(必做题)
1、在Rt△ABC中,∠C=90°, (1)AC=25,AB=27,求tanA和tanB
(2)BC=3,tanA=0.6,求AC 和AB。
(3)AC=4,tanA=0.8,求BC。
2、在梯形ABCD中,AD//BC,AB=DC=13,AD=8, BC=18,求tanB。挑战自己:(选做题) 1、在△ABC中,D是AB的中点,DC⊥AC,tan∠BCD=0.5,AB=4 ,求AC。谢谢听课试一试: 如图表示两个自动扶梯,哪一个自动扶梯比较陡? 甲 乙
