篮球中的二次函数[下学期]

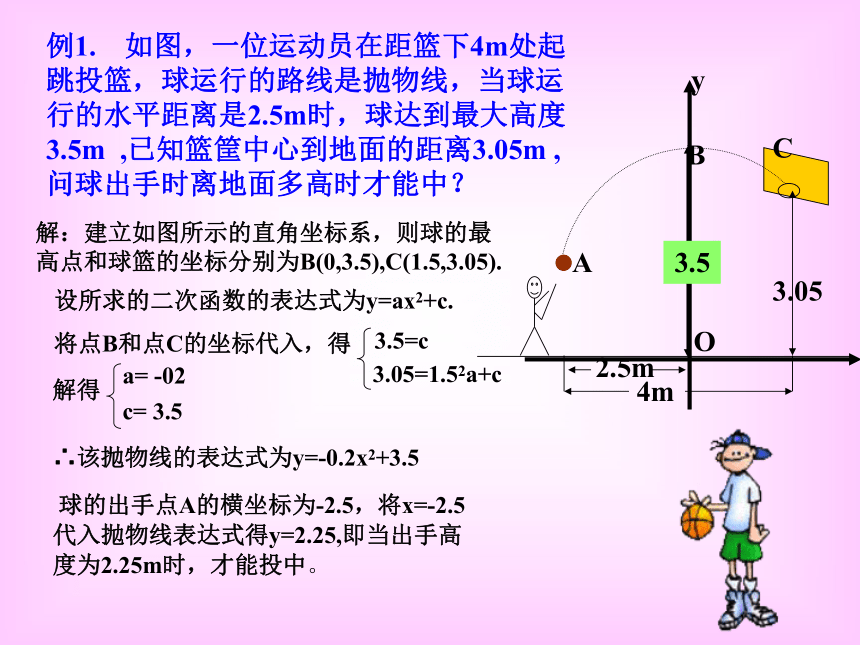
课件8张PPT。篮球中的二次函数例1. 如图，一位运动员在距篮下4m处起跳投篮，球运行的路线是抛物线，当球运行的水平距离是2.5m时，球达到最大高度3.5m ,已知篮筐中心到地面的距离3.05m , 问球出手时离地面多高时才能中？ 球的出手点A的横坐标为-2.5，将x=-2.5代入抛物线表达式得y=2.25,即当出手高度为2.25m时，才能投中。解：建立如图所示的直角坐标系，则球的最 高点和球篮的坐标分别为B(0,3.5),C(1.5,3.05).
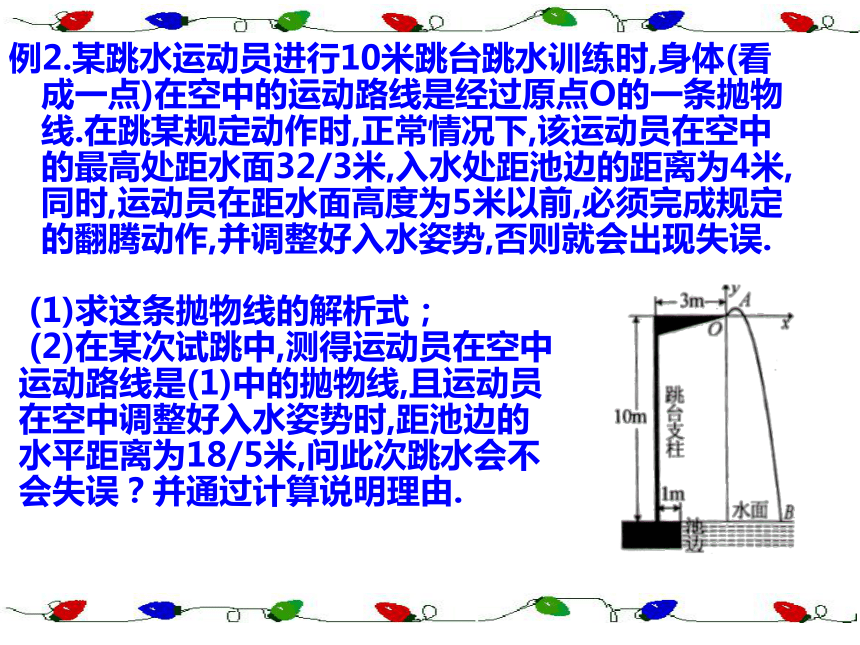
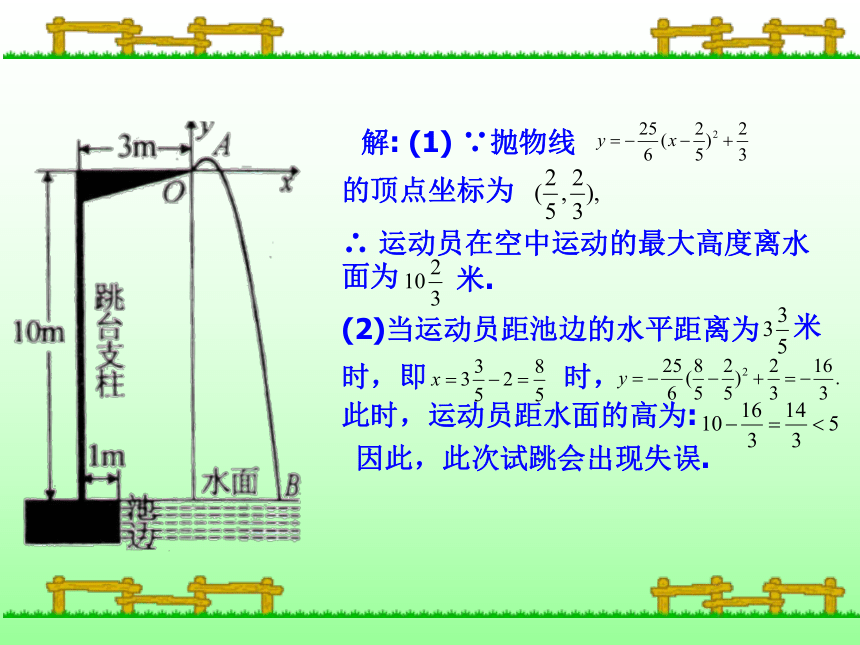
例2.某跳水运动员进行10米跳台跳水训练时,身体(看成一点)在空中的运动路线是经过原点O的一条抛物线.在跳某规定动作时,正常情况下,该运动员在空中的最高处距水面32/3米,入水处距池边的距离为4米,同时,运动员在距水面高度为5米以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.
(1)求这条抛物线的解析式；
(2)在某次试跳中,测得运动员在空中
运动路线是(1)中的抛物线,且运动员
在空中调整好入水姿势时,距池边的
水平距离为18/5米,问此次跳水会不
会失误？并通过计算说明理由.练习1 市植物园人工湖上有抛物线型拱桥，正常水位时桥下水面宽20米，拱高4 米，根据此条件建立如图所示坐标系，得知此时抛物线的解析式为 y= － x2+4
①在正常水位基础上水位上升 h 米时，桥下水面宽为d 米，求d与h 函数关系式。
②正常水位时，桥下水深2米，为了保证游船顺利通过，桥下水面宽不得小于18 米,求水深超过多少会影响过往游船在桥下顺利航行？练习2.某公园草地的护栏是由50段形状相同的抛物线组成的，为牢固起见，每段护栏需按间距0.4m加设立柱。为计算所需钢管立柱的总长度，设计人员建立如下坐标系计算。
(1)求抛物线解析式;
(2)自变量x的取值范围求;
(3)总长度。　小　结实际问题 数学问题求解数学问题谢谢