与圆有关的动点问题[下学期]
图片预览

文档简介
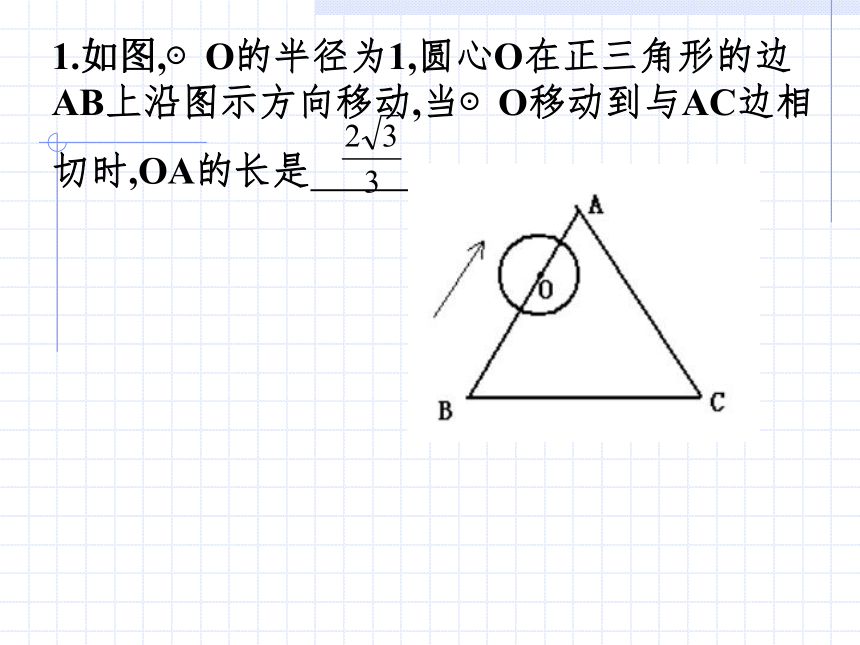
课件9张PPT。与圆有关的动点问题初三数学组1.如图,⊙O的半径为1,圆心O在正三角形的边AB上沿图示方向移动,当⊙O移动到与AC边相
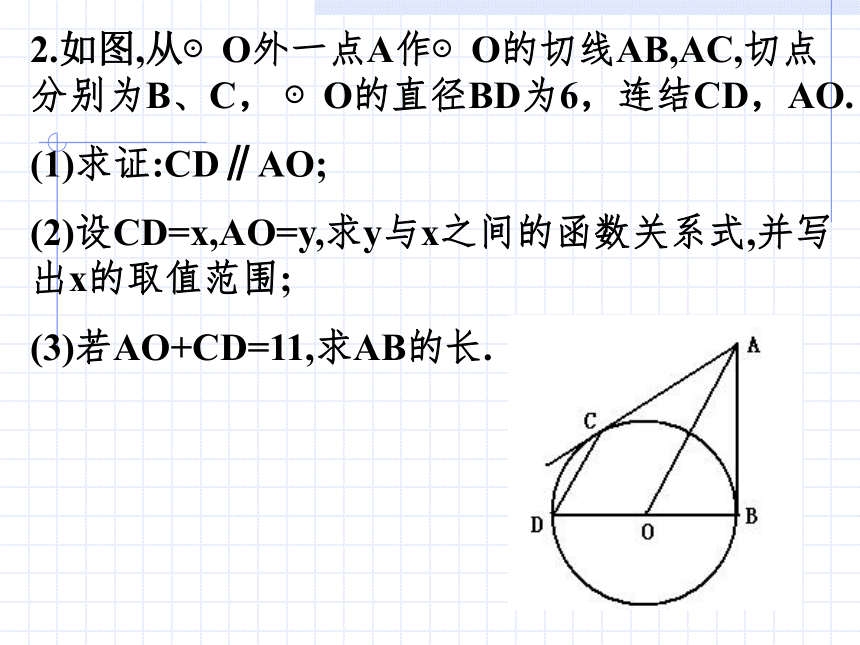
切时,OA的长是 .2.如图,从⊙O外一点A作⊙O的切线AB,AC,切点分别为B、C, ⊙O的直径BD为6,连结CD,AO.
(1)求证:CD∥AO;
(2)设CD=x,AO=y,求y与x之间的函数关系式,并写出x的取值范围;
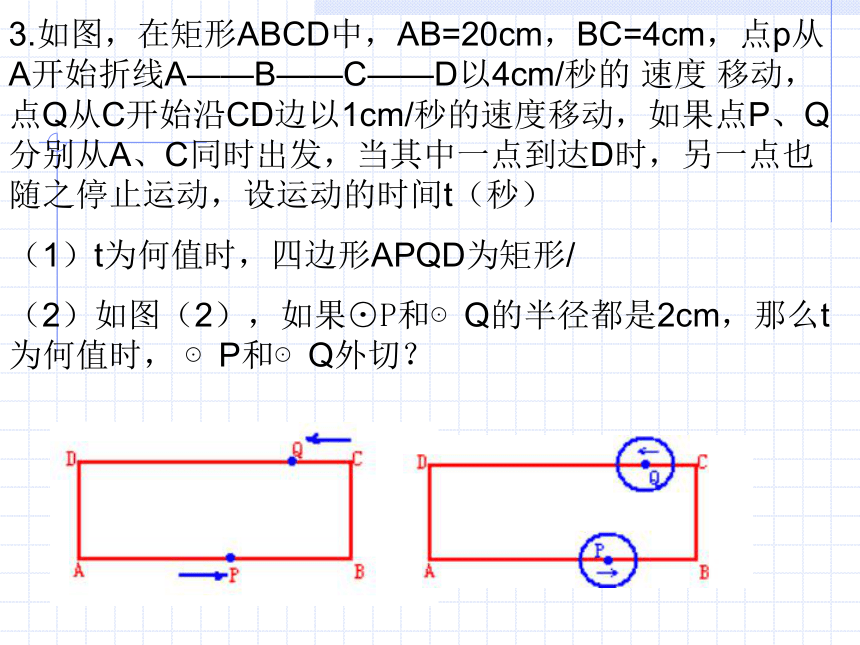
(3)若AO+CD=11,求AB的长.3.如图,在矩形ABCD中,AB=20cm,BC=4cm,点p从A开始折线A——B——C——D以4cm/秒的 速度 移动,点Q从C开始沿CD边以1cm/秒的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达D时,另一点也随之停止运动,设运动的时间t(秒)
(1)t为何值时,四边形APQD为矩形/
(2)如图(2),如果⊙P和⊙Q的半径都是2cm,那么t为何值时, ⊙P和⊙Q外切?4.例 如图,点E为正方形ABCD中BC上一动点,正方形
边长为1,以AE为直径作圆,圆心为O. (1)设BE=x, ⊙O的面积为y, 求y与x的函数关系及定义域. (2)BE为何值时⊙O与CD相切. (3)在(2)的条件下切点F在CD的 位置如何,并加以证明. (4)问以CD为直径的圆是否与(2) 条件下的AE相切,说明理由.解: (1)正方形ABCD中,AE2=BE2+AB2,
BE=x,AB=1,∴ AE2=x2+1 (0≤x≤1).(2)作OF⊥CD,垂足为F,显然AD∥OF∥CE∵AO=OE∴ CF=DF,FO是梯形ADCE的中位线F若⊙O与CD相切必有 (2FO)2=BE2+AB2AE2=BE2+AB2(2-x)2=x2+124-4x+x2=x2+1(3)从(2)可得F是CD的中点(4)作FH⊥AE于H∵OF∥BC∴∠1=∠2,∠FHO=∠B=90°∴△OFH∽△EAB∵OF∥BC∴FD=FH∴AE与以CD为直径的圆F相切.HF12如图,半圆O直径DE=12,Rt△ABC中,BC=12,∠ACB=900, ∠ACBC=300.半圆O以每秒2个单位从左到右运动,在运动过程中,点D,E始终在直线BC上,设运动时间为t秒.当t=0时,半圆O在△ABC的左侧,OC=8.
(1)当t为何值时,△ABC的一边与半圆O所在的圆相切?
(2)当△ABC的一边与半圆O所在的圆相切时,如果半圆O与直径DE围成的区域与△ABC的三边围成的区域有重叠部分,求重叠部分的面积.练一练小结:1.复习整理所学圆的知识,注意前后知识的衔接. 2.解题要注重审题.在了解所用知识和产生解题方案过程中,适时关注数学思想方法运用. 3.在解决问题过程中,积极联想,主动探究,形成再发现和再创造. 4.在复习本章知识同时,要善于其他章的知识的综合,如代数、三角及几何中的相似形等知识的链接.
切时,OA的长是 .2.如图,从⊙O外一点A作⊙O的切线AB,AC,切点分别为B、C, ⊙O的直径BD为6,连结CD,AO.
(1)求证:CD∥AO;
(2)设CD=x,AO=y,求y与x之间的函数关系式,并写出x的取值范围;
(3)若AO+CD=11,求AB的长.3.如图,在矩形ABCD中,AB=20cm,BC=4cm,点p从A开始折线A——B——C——D以4cm/秒的 速度 移动,点Q从C开始沿CD边以1cm/秒的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达D时,另一点也随之停止运动,设运动的时间t(秒)
(1)t为何值时,四边形APQD为矩形/
(2)如图(2),如果⊙P和⊙Q的半径都是2cm,那么t为何值时, ⊙P和⊙Q外切?4.例 如图,点E为正方形ABCD中BC上一动点,正方形
边长为1,以AE为直径作圆,圆心为O. (1)设BE=x, ⊙O的面积为y, 求y与x的函数关系及定义域. (2)BE为何值时⊙O与CD相切. (3)在(2)的条件下切点F在CD的 位置如何,并加以证明. (4)问以CD为直径的圆是否与(2) 条件下的AE相切,说明理由.解: (1)正方形ABCD中,AE2=BE2+AB2,
BE=x,AB=1,∴ AE2=x2+1 (0≤x≤1).(2)作OF⊥CD,垂足为F,显然AD∥OF∥CE∵AO=OE∴ CF=DF,FO是梯形ADCE的中位线F若⊙O与CD相切必有 (2FO)2=BE2+AB2AE2=BE2+AB2(2-x)2=x2+124-4x+x2=x2+1(3)从(2)可得F是CD的中点(4)作FH⊥AE于H∵OF∥BC∴∠1=∠2,∠FHO=∠B=90°∴△OFH∽△EAB∵OF∥BC∴FD=FH∴AE与以CD为直径的圆F相切.HF12如图,半圆O直径DE=12,Rt△ABC中,BC=12,∠ACB=900, ∠ACBC=300.半圆O以每秒2个单位从左到右运动,在运动过程中,点D,E始终在直线BC上,设运动时间为t秒.当t=0时,半圆O在△ABC的左侧,OC=8.
(1)当t为何值时,△ABC的一边与半圆O所在的圆相切?
(2)当△ABC的一边与半圆O所在的圆相切时,如果半圆O与直径DE围成的区域与△ABC的三边围成的区域有重叠部分,求重叠部分的面积.练一练小结:1.复习整理所学圆的知识,注意前后知识的衔接. 2.解题要注重审题.在了解所用知识和产生解题方案过程中,适时关注数学思想方法运用. 3.在解决问题过程中,积极联想,主动探究,形成再发现和再创造. 4.在复习本章知识同时,要善于其他章的知识的综合,如代数、三角及几何中的相似形等知识的链接.
