二次函数的应用[下学期]

课件14张PPT。二次函数的应用中考复习专题 已知二次函数y= ax2＋bx+c的图象如图所示，且OA=OC，由抛物线的特征请尽量多地写出一些含有a、b、c三个字母的等式或不等式：xyoAB-11-1C 1、 在平面直角坐标系中，有一个二次函数的图象交 x 轴于（-4，0），（2，0）两点，现将此二次函数图象向右移动 h 个单位，再向上移动 k 个单位，发现新的二次函数图象与x轴相交于（-1，0），（3，0）两点，则h的值为（ ）
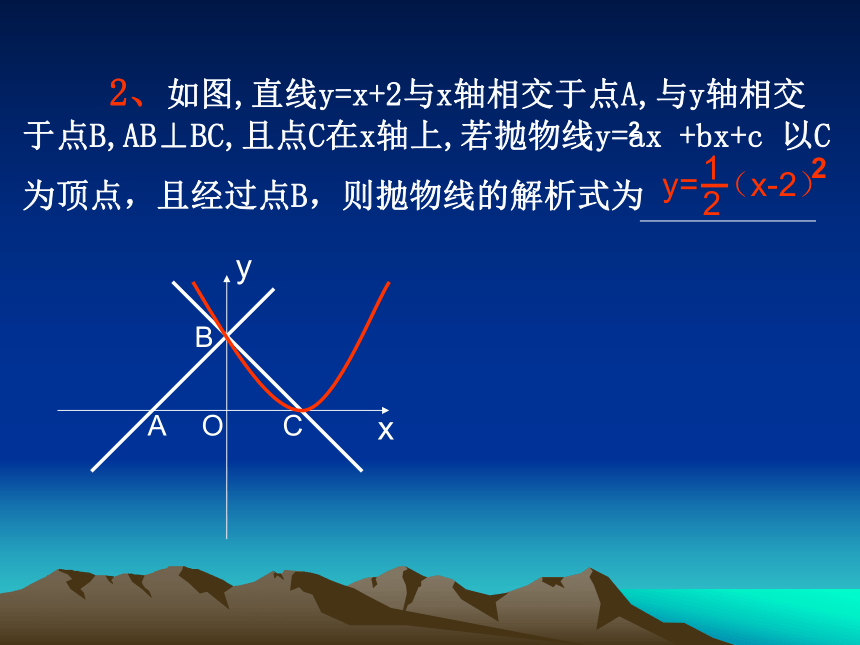
（A）0 （B）1 （C）2 （D）4C 2、如图,直线y=x+2与x轴相交于点A,与y轴相交于点B,AB⊥BC,且点C在x轴上,若抛物线y=ax +bx+c 以C
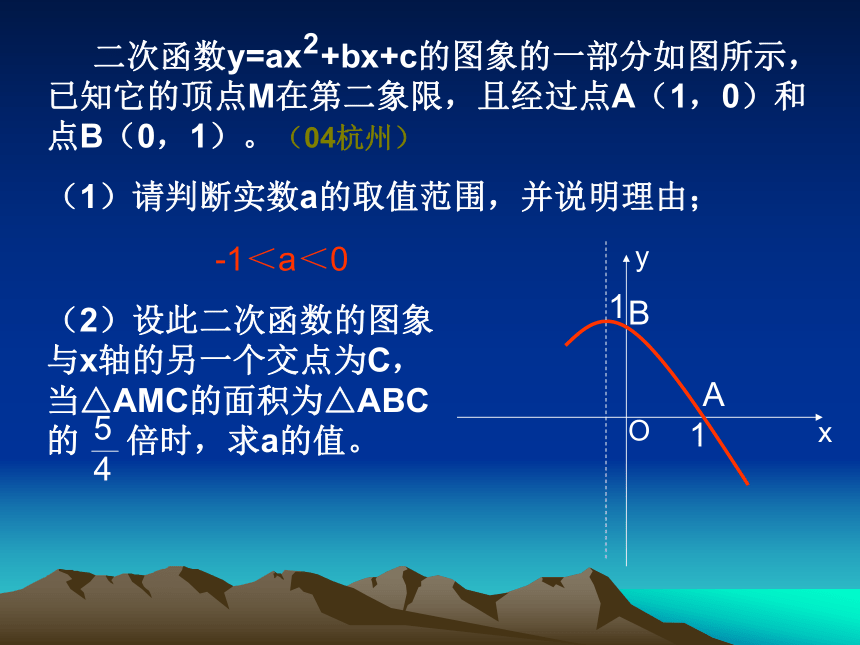
为顶点，且经过点B，则抛物线的解析式为 2ABCxyO 二次函数y=ax +bx+c的图象的一部分如图所示，已知它的顶点M在第二象限，且经过点A（1，0）和点B（0，1）。（04杭州）
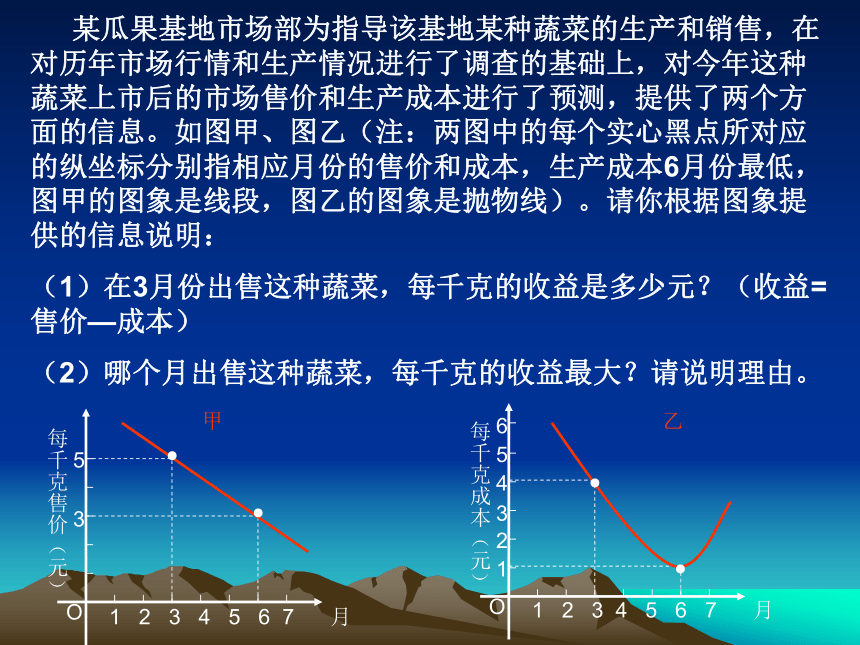
（1）请判断实数a的取值范围，并说明理由；2xy1B1AO-1＜a＜0 某瓜果基地市场部为指导该基地某种蔬菜的生产和销售，在对历年市场行情和生产情况进行了调查的基础上，对今年这种蔬菜上市后的市场售价和生产成本进行了预测，提供了两个方面的信息。如图甲、图乙（注：两图中的每个实心黑点所对应的纵坐标分别指相应月份的售价和成本，生产成本6月份最低，图甲的图象是线段，图乙的图象是抛物线）。请你根据图象提供的信息说明：
（1）在3月份出售这种蔬菜，每千克的收益是多少元？（收益=售价—成本）
（2）哪个月出售这种蔬菜，每千克的收益最大？请说明理由。1 2 3 4 5 6 7 月每千克售价（元）5
3O1 2 3 4 5 6 7 月每千克成本（元）5
3O1246●●●●甲乙练习2、已知：用长为12cm的铁丝围成一个矩形，一边长为xcm.,面积为ycm2,问何时矩形的面积最大？解： ∵周长为12cm, 一边长为xcm , ∴ 另一边为（6－x）cm
解:由韦达定理得：x1＋x2＝2k ，x1?x2＝2k－1
∴ y＝x（6－x）＝－x2＋6x （0< x<6）
＝－(x－3) 2＋9
∵ a＝－1<0, ∴ y有最大值
当x＝3cm时，y最大值＝9 cm2，此时矩形的另一边也为3cm答：矩形的两边都是3cm，即为正方形时，矩形的面积最大。next例1:如图，在一面靠墙的空地上用长为24米的篱笆，围成中间隔有二道篱笆的长方形花圃，设花圃的宽AB为x米，面积为S平方米。
(1)求S与x的函数关系式及自变量的取值范围；
(2)当x取何值时所围成的花圃面积最大，最大值是多少？
(3)若墙的最大可用长度为8米，则求围成花圃的最大面积。 解： (1) ∵ AB为x米、篱笆长为24米
∴ 花圃宽为（24－4x）米
(3) ∵墙的可用长度为8米
∴ S＝x（24－4x）
＝－4x2＋24 x （0∴ 0<24－4x ≤6 4≤x<6∴当x＝4cm时，S最大值＝32 平方米例2：某高科技发展公司投资500万元,成功研制出一种市场需求量较大的高科技替代产品,羡慕投入资金1500万元进行批量生产,已知行产每件产品的成本为40元,在销售过程中发现:当销售单价定为100元时,一年的销售量为20万件;销售单价每增加10元,年销售量就减少1万件.设销售单价为x（元），年销售量为y（万件），年获利（年获利=处销售额－生产成本－投资）为z（万元）。（4）公司计划：在第一年按年获利最大确定的销售单价，进行销售；第二年年获利不低于1130万元，请你借助函数的大致图像说明，第二年的销售单价x（元），应确定在什么范围。（3）计算销售单价为160元时的年获利，并说明同样的年获利，销售单价还可以定为多少元？相应的年销售量分别为多少万件？ 例 心理学家研究发现，一般情况下，学生的注意力随着教师讲课时间的变化而变化，讲课开始时，学生的注意力初步增强，中间有一段时间学生的注意力保持较为理想的状态，随后学生的注意力开始分散，经过实验分析可知，学生的注意力y随时间t的变化规律有如下关系（04黄冈）（1）讲课开始后第5分钟与讲课开始第25分钟比较，何时学生的注意力更集中？（2）讲课开始后多少分钟，学生的注意力最集中？能持续多少分钟？（3）一道数学题，需要讲解24分钟，为了效果较好，要求学生的注意力达到180，那么经过适当安排，老师能否在注意力达到所需的状态下讲解完这道题目？ 有一种螃蟹，从海上捕获后不放养最多只能存活两天，如果放养在塘内，可以延长存活时间，但每天也有一定数量的蟹死去。假设放养期内蟹的个体重量基本保持不变。现有一经销商，按市场价收购了这种活蟹1000千克放养在塘内，此时的市场价为每千克30元。据测算，此后每千克活蟹的市场价每天可上升1元，但是，放养一天需各种费用支出400元，且平均每天还有10千克蟹死去，假定死蟹均于当天全部售出，售价都是每千克20元。 （1）设x天后每千克活蟹的市场价为P元，写出P关于x的函数关系式； （2）如果放养x天后将活蟹一次性出售，并记1000千克蟹的销售总额为Q元，写出Q与x的函数关系式； （3）该经销商将这批蟹放养多少天后出售，可获最大利润（利润＝销售总额－收购成本－费用）？增大利润是多少？ 例2:如图，等腰Rt△ABC的直角边AB＝２，点P、Q分别从A、C两点同时出发，以相等的速度作直线运动，已知点P沿射线AB运动，点Q沿边BC的延长线运动，PQ与直线相交于点D。
(1)设 AP的长为x，△PCQ的面积为S，求出S关于x的函数关系式；
(2)当AP的长为何值时，S△PCQ= S△ABC 解：（１）∵P、Q分别从A、C两点同时出发，速度相等当P在线段AB上时 ∴AP=CQ=x动画演示当P在线段AB的延长线上时 (2)当S△PCQ＝S△ABC时，有此方程无解