圆中的角[下学期]

课件11张PPT。转化灵活的圆中角
科学的灵感，决不是等待可以等来的，只能给那些有素养的人，给那些善于独立思考的人，给那些具有锲而不舍的精神的人
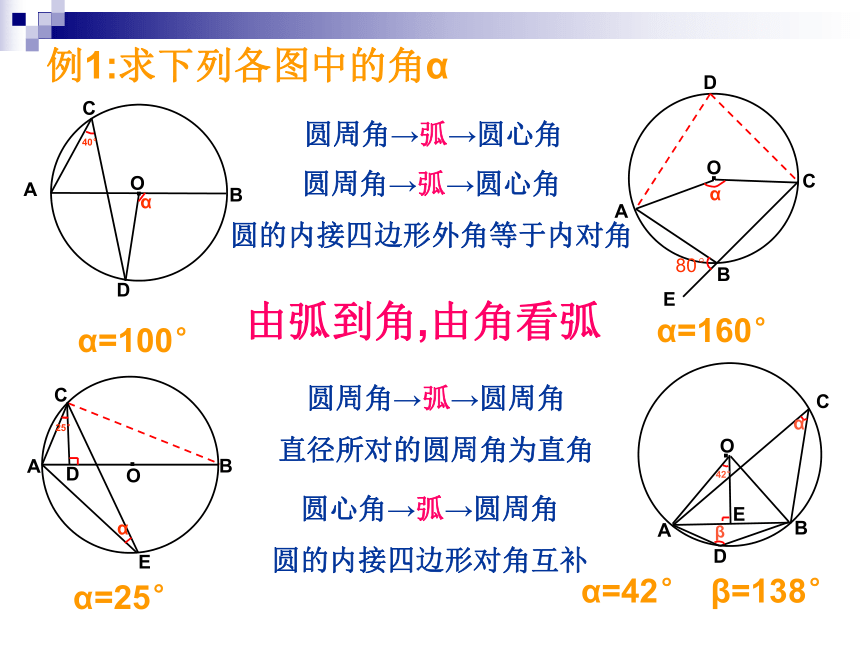
角是几何图形中最重要的元素,证明两直线位置关系,运用全等三角形法,相似三角形法都要涉及角,而圆的特征,赋予角极强的活性,使得角能 .灵活地互相转化例1:求下列各图中的角αO.EBD80°αα=100°α=160°α=25°β=138°圆周角→弧→圆心角圆周角→弧→圆心角
圆的内接四边形外角等于内对角
圆周角→弧→圆周角
直径所对的圆周角为直角
圆心角→弧→圆周角
圆的内接四边形对角互补
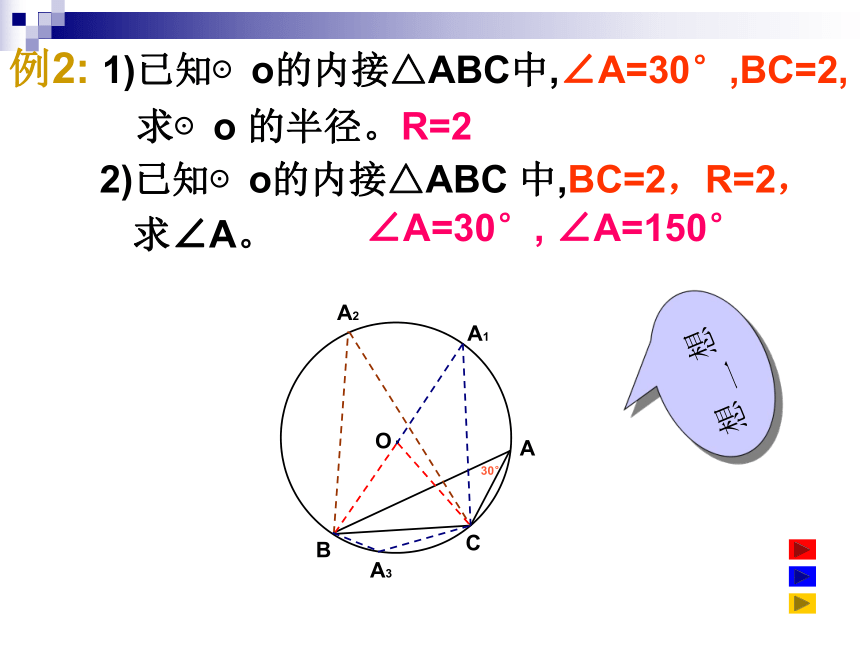
α=42°由弧到角,由角看弧例2: 1)已知⊙o的内接△ABC中,∠A=30°,BC=2,
求⊙o 的半径。
ABCOA2A1A330° 2)已知⊙o的内接△ABC 中,BC=2，R=2，
求∠A。. 想
一
想R=2∠A=30°, ∠A=150°
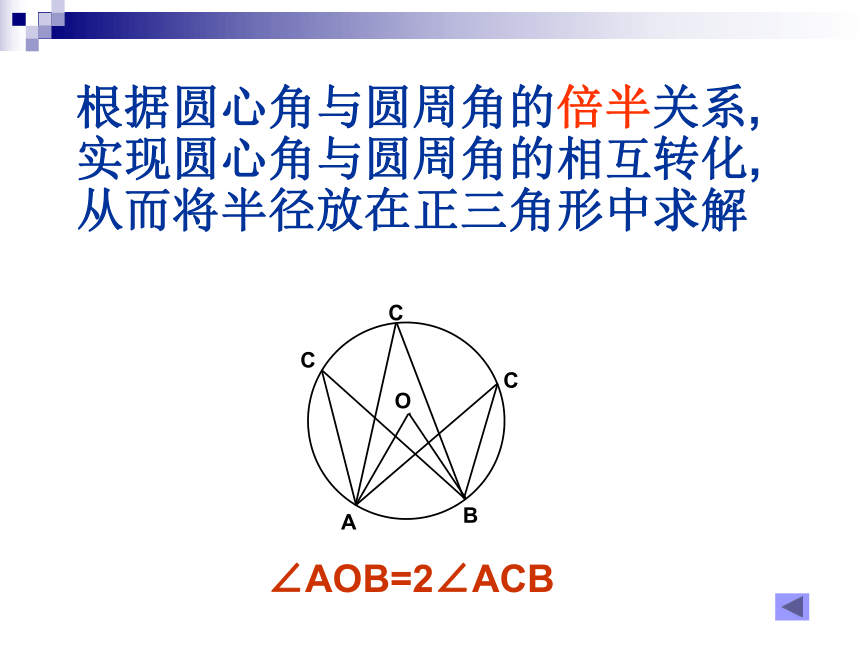
根据圆心角与圆周角的倍半关系,实现圆心角与圆周角的相互转化,从而将半径放在正三角形中求解CAOB.CC∠AOB=2∠ACB 根据同弧(或等弧)所对圆周角相等,将圆周角在大小不变的情况下,改变顶点在圆上的位置,将角相互转化,而直径所对的圆周角为直角,从而将半径放在直角三角形中求解B.C1ABCC1.ACC1oo∠ACB=90° ∠ACB=∠AC1B例3、已知：如图，AB是半圆的直
径，AC是一条弦，D是弧AC
的中点，DE⊥AB于E交AC于F，
DB交AC于G，
求证：AF=FGADEBFGCO..5123467例4:如图，已知⊙o1和⊙o2相交于点A、B,P
是⊙o1上的任意一点,PA、PB的延长线交
⊙o2于点C、D。 ⊙o1的直径PE的延长
线交CD于点M。
求证：PM⊥CDABPMEDCO2O1..思考:（1）如图，AB是⊙o的直径，CD与AB相
交于点E， ∠ACD=60°,∠ADC=50°,则
∠AEC为多少度。 （2）如图,等边△ABC的外接圆弧BC上任意
一点P,CP的延长线和AB的延长线交于点D,
求证: ∠D= ∠CBP。 B
1、根据圆心角与圆周角的倍分关系,可实现圆心
角与圆周角的转化;
2、由同弧所对的圆周角相等,可将圆周角在大小
不变的情况下,改变顶点在圆上位置进行探索;3、由圆内接四边形的对角互补和外角等于内对
角,可将与圆有关的角互相联系起来.4、在圆中角的相互转化中,弧是联系与圆有关的
角的中介,“由弧到角,由角看弧”是促使与圆有
关的角互相转化的基本方法。
下课了再见